Enthalpy Changes During Phase Transformations | Additional Study Material for JEE PDF Download
Kirchoff's Equation
This gives the relation between enthalpy and temperature.
- Physical state is changed at constant temperature.
According to Hess'Law
ΔH2 + Cp(T2-T1) = ΔH1 + Cp1 (T2- T1)
ΔH2 - ΔH1 = (Cp1 - Cp) (T2- T1)
= ΔCp (T2- T1)
Where
ΔCp = Molar heat capacity of product -- Molar heat capacity of reactant
Example:
N2(g) + 3H2(g) ⇒ 2NH3(g)
ΔCp = 2Cp(NH3) - Cp(N2) - 3Cp(H2)
- If the above formula (Kirchoff's eqn) is to be written for molar heat capacity at constant volume then
a
- If ΔCp is function of temperature
ΔCp = T2 + T
Then
Heat of formation
Enthalpy change during the formation of 1 mole of a compound form its most stable common occurring form (also called reference states) of elements is called heat of formation.
C(s) + O2(g) ⇒ CO2(g)
ΔH = ΔHf(CO2)
CO(g) + 1/2O2(g) ⇒ CO2(g)
ΔH ≠ ΔHf(CO2)(g)
(because CO2 has not been formed form its element in their most stable form)
Similarly
Heat of reaction
Element | Most stable form |
H | H2(gas) |
O | O2(gas) |
N | N2(gas) |
F | F2(gas) |
Cl | Cl2(gas) |
Br | Br2(gas) |
I | I2(solid) |
C | C(grapnite) |
P | P(white) |
S | S(rhombic) |
- All metal except Hg exist in solid form (reference states)
Enthalpy At Standard State :-(ΔHº)
T = 25ºC = 298 K
P = 1 atm
Conc = 1M
ΔHº = Heat of formation at standard state
If A(g) + B(g) ⇒ C(g +D(g) is any reaction, Heat of reaction for any thermochemical equation can be written as
ΔHº = DHfº(product) - DHfº(Reactant)
If we use the above concept for the above given reaction then
ΔHº = DHfº(c) + ΔHfº(D) - ΔHfº(A) + ΔHfº(B)
Assumption:
The heat of formation of most stable form of an element is taken as zero.
C(graphite) + O2(g) ⇒ CO2(g)
ΔHº = ΔHfº(CO2) - ΔHfºC(s) - ΔHfº(O2)(g)
⇒ ΔHº = ΔHfº(CO2) (As ΔHfºC(s) = 0 and Δ HfºO2(g) = 0)
Another example can be taken as
H2(g) + 1/2O2(g) ⇒ H2O(l)
Ex.1 From the following data,
C(s, graphite) O2(g) ⇒ CO2(g) DHº = -393.5 kJ/mole
H2(g) + 1/2O2(g) ⇒ H2O(l) DHº = -286 kJ/mole
2C2H6(g) + 7O2(g) ⇒ 4CO2(g) 6H2O(l) ΔHº = -3120 kJ/mole
Calculate the standard enthalpy of formation of C2H6(g) (in kJ/mole)
Sol. From eqn(1) ΔHfº(CO2) = -393.5 kJ/mole
From eqn(2) ΔHfº(H2O) = -286 kJ/mole
From eqn (3) ΔrHº = 4 ΔHfº(CO2) + 6ΔHfº(H2O) -2 ×ΔHfº(C2H6 ) - 7×ΔHfºO2(g)
- 3120 = 4 ×(-393.5) + 6×(-286) - 2×ΔHfº(C2H6 ) (As ΔHfº O2(g) = 0 )
⇒ -3120 = -1574 -1716 - 2 ×ΔHfº(C2H6 )
⇒ -3120 + 3290 = - 2 ×ΔHfº(C2H6 )
⇒ 170 = - 2 ×ΔHfº(C2H6 )
⇒ ΔHfº = - 85 kJ/mole
Heat of Combustion
It is the enthalpy change (always -ve) when One mole of the substance undergo complete combustion.
C(s) + O2 ⇒ CO2(g)
ΔHº = ΔHCºC(s) = ΔHfº(CO2) - ΔHfºC(s) - ΔHfº(O2)
ΔHº = = ΔHC ºC(s) = ΔHfº(CO2)
Other example
Note :
Heat of combustion is always exothermic
- N2 + O2 ⇒ 2NO (It is an endothermic reaction)
- O2 + F2 ⇒ OF2 (Since O has normally tendency to accept electron and opposite is happening above hence reaction is is considered endothermic)
- Heat of reaction for any thermochemical equation can be written as (in form of heat of combustion)
ΔHrº = Heat of combustion of reactant - Heat of combustion of reactant.
ΔHrº = ΔHCº (Reactant) - ΔHCº (Product)
Ex.2 The enthalpy change for the reaction
C3H8(g) + H2(g) ⇒ C2H6(g) + CH4(g) at 25ºC is - 55.7 kJ/mole calculate the enthalpy of combustion of C2H6(g). The enthalpy of combustion of H2, and CH4 are - 285.8 and - 890.0 kJ/mole respectively. Enthalpy of combustion of propane is -2220 KJmol-1.
Sol. As we know any thermochemical eqn can be written in terms of heat of combustion as follows
ΔHrº = ΔHcº (Reactant) - ΔHCº (Product)
ΔHrº = ΔHcº (C3H8) +ΔHCº (H2) - {ΔHcº(C2H6)+ ΔHCº(CH4) }
- 55.7 = (-2220 - 285.8) - {-890 +ΔHcº(C2H6) }
⇒ ΔHcº(C2H6) (g) = - 1560.1 kJmol-1
Problems Based on Both HOC and HOF :
Ex.3 At 300K, the standard enthalpies of formation of C6H5COOH(s), CO2(g) and H2O(l) are -408, -393 and -286 kJmol-1 respectively. Calculate the enthalpy of combustion of benzoic acid at
(i) constant pressure
(ii) constant volume.
Sol.
7C(s) + 3H2(g)+ O2(g) ⇒ C6H5COOH(s) ΔHº = -408 kJ
⇒ ΔHfº(C6H5COOH) = - 408 kJ
C(s) + O2(g) ⇒ CO2(g) ΔHº = -393 kJ
⇒ ΔHfº(CO2) = -393 kJ
H2(g) + 1/2O2(g) ⇒ H2O(l) ΔHº = -286 kJ
⇒ ΔHfº(H2O) = -286 kJ
C6H5COOH(s) + 15/2O2(g) ⇒ 7CO2(g) + 3H2O(l)
⇒ ΔHCº(C6H5COOH) = 7 ΔHfºCO2 + 3ΔHfº(H2O) - 4ΔHfº(C6H5COOH)
= 7 ×(-393) 3× (-286) 408
ΔHCº(C6H5COOH) = - 3609 408
= -3201 kJ/mol
⇒ enthalpy of combustion at constant pressure = - 3201 kJ mol-1
Also
ΔH = ΔU + ΔngRT
-3201 = ΔU + (-0.5) × 8.31 × 10-3 × 300
(As Δn = 0.5, R = 8.314 × 10-3 kJ)
⇒ ΔU = - 3201 + 1.2471
ΔU = -3199.7529
⇒ enthalpy of combustion at constant volume = - 3199.7529 kJ mol-1
Bond Energy
It is defined for gaseous molecules. "The enthalpy change during the breaking of one mole of bond into isolated gaseous atoms is called bond energy of the compound"
Example:
H2(g) ⇒ 2H(g) , ΔHº = Σ H-H
ΔHº = Σ H-H = 2ΔHfºH(g) - ΔHfº(H2)
Similarly
- Let us consider the similar bond breaking In CH4
CH4(g) ⇒ C(g) + 4 H(g)
ΔH = 4 ΣC-H =ΔHfºC(g) 4ΔHfºH(g) - ΔHfº(CH4) - Enthalpy of reaction in terms of bond energy for a thermochemical eqn can be written as
ΔHfº = B.E.(Reactant) - B.E. (products)
Ex.4 Using the bond enthalpy data given below, calculate the enthalpy change for the reaction
C2H4 (g) + H2(g) ⇒ C2H6(g)
Data:
Sol.
ΔrHº = Σreactant - Σproduct
ΔHrº = ΣC = C+4 ΣC-H + ΣH-H- ΣC-C-6 ΣC-H
ΔHrº = 606.68 4×410.87 431.79 -336.81 -6×410.87 = 2681.95 -2802.03
ΔHrº = -120.08 kJ/mol
Heat of hydrogenation
"Enthalpy change during the addition of 1 mole of H2 to an unsaturated compound. is called heat of hydrogenation."
Hydrogenation is an exothermic process. of therefore heat of hydrogenation is always -ve.
Example:
CH2 = CH2 + H2 ⇒ CH3 -CH3
ΔHrº = ΔHº (Hydrogenation of CH2 = CH2)
ΔHrº = ΔHº (Hydrogenation) of cyclohexene
Ex.5 Compare the heat of hydrogenation of the following alkene
(1) C - C - C = C
(2) C - C = C - C (cis)
(3) C - C = C - C (trans)
(4) C - = C
(5) C = C - C = C
Sol. 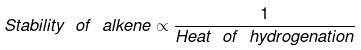
The above concept is true as long as no. of double bonds are equal as heat of hydrogenation is defined for per mole of double bond. It will be certainly larger for higher number of double bonds irrespective of their stability.
(1) C - C - C = C (2 × H)
(2) C - C = C - C ( 6 × H)
(cis)
(3) C - C = C - C (6 × H)
(trans)
(4) C = C (6 × H)
(5) C = C - C = C (2 double bonds)
As we know trans > cis (stability)
⇒ Heat of hydrogen (trans) < Heat of hydrogenation (cis)
of therefore decreasing order of heat of hydrogenation of alkene 5 > 1 > 2 > 3 > 4
Ex.6 Find DHf of HCl(g) if bond energies of H2, Cl2 and HCl are 104, 58, 103 kcal/mole respectively.
Sol. H - Cl ⇒ H(g) + Cl(g)
ΣH-Cl = ΔHfºH(g) + HfºCl(g) - ΔHfºHCl(g)
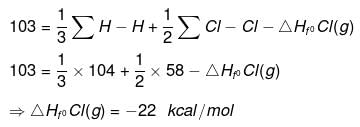
Heat of Atomisation
" When one mole of any substance is converted into gaseous atoms enthalpy change during the process is called heat of atomisation." It is always +ve.
Heat of sublimation
Enthalpy change during the conversion of one mole of solid to 1 mole of gaseous phase directly without undergoing into liquid phase is called enthalpy of sublimation or heat of sublimation,
It is always +ve due to endothermic nature of the process.
Example:
C(s) ⇒ C(g)
ΔHº = ΔHsubºC(s) = ΔHfº C(g) - ΔHfº C(s)
⇒ ΔHsubºC(s) = ΔHfº C(g)
⇒ ΔHsubºC(s) = ΔHfº C(g) = ΔHºatmosationC(g)
Ex.7 Using the given data, calculate enthalpy of formation of acetone(g) [All values in kJmol-1] bond enthalpy of C-H = 413.4, C - C = 347.0 (C = O) = 728.0
O = O = 495.0 , H - H = 435.8 DsubH of C = 718.4
Sol. 3C(g) + 6H(g) + O(g)
6 ΣC-H + Σ C-O + 2 Σ C-C = 3DHfºC(g) + 6ΔHfºH(g) + ΔHfºO(g) - ΔHfº()
6 × 413.4+728 + 2 × 347 = 3 × 718.4 + 6/2 × 435.8 + 1/2 ×495.0 - ΔHfº()
⇒ ΔHfº() = - 192.3 kJmol-1
Ex.8 The enthalpy of combustion of acetylene is 312 kcal. If enthalpy of formation of CO2 and H2O are -94.38 and -68.38 kcal respectively.
Calculate  bond enthalpy.
bond enthalpy.
Given that enthalpy of atomisation of 150 kcal and H - H bond enthalpy and C - H bond enthalpy are 103 kcal and 93.64 kcal respectively.
Sol. HC ≡ CH + 5/2O2 ⇒ 2CO2 + H2O
ΔHCº(CH ≡ CH) = 2ΔHfº(CO2) + ΔHfº(H2O) - ΔHfº(C2H2)
- 312 = 2 × (-94.38) + (-68.38) - ΔHfº(C2H2)
ΔHfº(C2H2) = 54.86
CH ≡ CH ⇒ 2C(g) + 2H(g)
Σ C ≡ C + 2 Σ C-H = 2ΔHfºC(g) + 2ΔHfºH(g) - ΔHfº(CH º CH)
Σ C ≡ C + 2 × 93.64 = 2 × 150 2 × (1/2) × 103 -54.86
⇒ Σ C = C = 160.86 kJmol-1
Resonance Energy
"The energy difference between resonance hybrid and most stable canonical structure is called resonance energy".Resonance energy is generally -ve as nature of the process is exothermic.
Ex.9 The enthalpy of formation of ethane, ethylene and benzene from the gaseous atoms are -2839.2, -2275.2 and -5506 kJmol-1 respectively. Calculate the resonance energy of benzene. The bond enthalpy of C - H bond is given as equal to 410.87 kJ/mol.
Sol.
2C(g) + 6H(g) ⇒ C2H6 ΔHº = -2839.2
C2H6 ⇒ 2C(g) + 6H(g) ΔHº = 2839.2
∑C - C + 6∑C - H = 2839.2 ΔHº = 2839.2
∑C - C + 6 × 410.87 = 2839.2
∑C - C = 373.98 ... (1)
2C(g) + 4H(g) ⇒ C2H4(g) ΔHº = -2275.2
C2H4 ⇒ 2C(g) + 4H(g) ΔHº = 2275.2
∑C = C + 4∑C - H = 2275.2
∑(C = C) = 631.72 ...(2)
6C(g) + 6H(g) ⇒ C6H6 ΔHº = -5506
⇒ C6H6 ⇒ 6C(g) + 6H(g) ΔHº = 5506
⇒ 3∑C = C + 3∑C - C + 6∑C - H+ x = 5506
Putting all the values from eqn , 1, & (2) we get x = 23.68
⇒ Resonance energy of benzene = - 23.68 kJ/mole
Bomb Calorimeter
Heat evolved = msΔt CΔt
Heat capacity of container

= - = -
= -
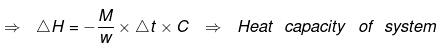
Ex.10 When 1.0 gm of fructose C6H12O6 (s) is burnt in oxygen in a bomb calorimeter, the temperature of the calorimeter water increases by 1.56ºC. If the heat capacity of the calorimeter and its contents is 10.0 kJ/ºC. Calculate the enthalpy of combustion of fructose at 298 K.
Sol.
Heat capacity of the system
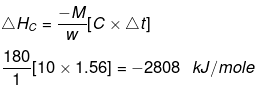
Heat of solution
Enthalpy change during the dissolution of 1 mole of salt in excess of solvent.
KCl(s) ⇒ KCl (aq)
ΔHº = Heat of soln of KCl (s)
Note :
(1) Heat of solution is always exothermic for the anhydrous form of salts which can form their hydrates.
Example:
CuSO4, Na2SO4, FeSO4, ZnSO4, CaCl2, LiCl etc.
CuSO4(s) aq ⇒ CuSO4(aq) ΔH < 0
(2) Heat of solution is endothermic for the hydrated form of the salt.
CuSO4 . 5H2O aq ⇒ CuSO4(aq) ΔH > 0
(3) Heat of soln is endothermic for the salts which do not form their hydrates.
Example:
NaCl, NaNO3, KCl etc.
Integral Heat of solution
Enthalpy change when 1 mole of salt is dissolved in given amount of solvent.
Example:
KCl(s) + 20 H2O ⇒ KCl (20H2O) -------------(1) DH2 = x
KCl(s) + 100 H2O ⇒ KCl (100H2O) -------------(2) DH2 = y
Heat of dilution
Reversing the eqn (1) and adding in (2)
KCl(20H2O) + 80H2O ⇒ KCl(100H2O)
ΔH = y - x
enthalpy change when the conc. of salt changes from one to another on the basis of dilution
⇒ ΔH = y - x = Heat of dilution
Heat of hydration
Ethalpy change during the formation of hydrated form of salt from its anhydrous form. It is always exothermic.
CuSO4(s) + 5H2O ⇒ CuSO4.5H2O
ΔH = Heat of hydration of CuSO4(s)
Ex.11 Heat of soln of CuSO4(s) and CuSO4.5H2O is 15.9 and 19.3 kJ/mol respectively. Find the heat of hydration of CuSO4(s)
Sol. CuSO4(s) + aq ⇒ CuSO4(aq) -----------(1)
ΔH = -15.9
CuSO4.5H2O + aq ⇒ CuSO4(aq) -----------(2)
ΔH = 19.3
Reversing eqn (1) and adding (2)
CuSO4(s) + aq ⇒ CuSO4(aq)
ΔH = 15.9
CuSO4.5H2O + aq ⇒ CuSO4(aq)
ΔH = 19.3
CuSO4.5H2O ⇒ CuSO4(s)
ΔH = 35.2
⇒ CuSO4(s) ⇒ CuSO4.5H2O
ΔH = -35.2
⇒ Heat of hydration of CuSO4(s) = -35.2 kJ/mol
Heat of neutralisation
Enthalpy change during neutralisation of 1 gm equivalent of Acid with 1 gm equivalent of base in dilute soln is called heat of neutralisation.
HCl(aq) + NaoH(aq) ⇒ NaCl + H2O
H + Cl- + Na + OH- ⇒ Na + Cl- + H2O
H (aq) + OH-(aq) ⇒ H2O(aq)
ΔHº = -13.7 Kcal
H2SO4(aq) + 2NaOH(aq) ⇒ Na2SO4 + 2H2O
2H + SO42- + 2Na + 2OH- ⇒ 2Na + SO42- + 2H2O
2H + 2OH- ⇒ 2H2O
⇒ ΔH = -13.7 × 2
Note :
In case of weak Acid or weak bases the observed value is little lower because of a part of it is used in dissociating weak Acid or weak base which is not at all completely ionised at dilute solution conditions.
These are however, completely ionised at infinite dilution.
Example:
CH3COOH + NaOH ⇒ CH3COONa + H2O
ΔH = -13.7 + x
As we know, H + OH- ⇒ H2O , ΔH = -13.7 kcal ----(1)
CH3COOH ⇒ CH3COO- + H , ΔHº = x ----(2)
Add eqn (1) (2)
CH3COOH + OH- ⇒ CH3COO- + H2O ΔHº = y
Ex.12 100 ml 0.5M H2SO4(strong Acid) is neutralised by 200 ml 0.2 M NH4OH. In a constant pressure calorimeter which results in temperature rise of 1.4ºC. If heat capacity of calorimeter constant is 1.5 kJ/ºC.
Which statement is/are correct.
Given: HCl + NaOH ⇒ NaCl + H2O 57 kJ
CH3COOH + NH4OH ⇒ CH3COONH4 + H2O 48.1 kJ
(A) Ethalpy of neutralisation of HCl v/s NH4OH is -52.5 kJ/mol
(B) Ethalpy of dissociation (ionisation) of NH4OH is 4.5 kJ/mol
(C) Ethalpy of dissociation of CH3COOH is 4.6 kJ/mol
(D) ΔH for 2H2O(l) ⇒ 2H+ (aq) + 2OH-(aq) is 114 kJ
Sol. (A) Total heat evolved due to the neutralization = C × Δt = 1.5 × 1.4 = 2.1
M. eq of H2SO4 = 100 ×0.5 = 50
M. eq of NH4OH = 20 × 0.2 = 40
Since NH4OH is limiting hence energy will evolved according to it.
⇒ 0.04 gm eq produces 2.1 kJ
1 gm eq produces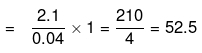
⇒ Heat of neutralisation = -52.5 kJ
(B) -57 + x = - 52.5
⇒ x = - 52.5 + 57 = 4.5
⇒ Enthalpy of dissociation of NH4OH = 4.5 kJ/mol
(C) 57-(x + y) = 48.1
⇒ x + y = 8.9
⇒ 4.5 y = 8.9 ⇒ y = 4.4
⇒ enthalpy of dissociation of CH3COOH = 4.4 kJ/mol
(D) As we know
H+ + OH- ⇒ H2O , ΔH = -57
⇒ 2H + 2OH- ⇒ 2H2O , ΔH = -57× 2
⇒ 2H2O ⇒ 2H++ 2OH- , ΔH = 114 kJ
⇒ Option A, B, and D are correct.
|
22 videos|163 docs|17 tests
|
FAQs on Enthalpy Changes During Phase Transformations - Additional Study Material for JEE
| 1. What is the definition of enthalpy? |  |
| 2. How do phase transformations affect enthalpy changes? |  |
| 3. What is the relationship between enthalpy and temperature during phase transformations? |  |
| 4. Are enthalpy changes reversible during phase transformations? |  |
| 5. Can enthalpy changes be measured experimentally during phase transformations? |  |
















