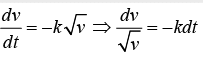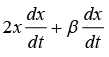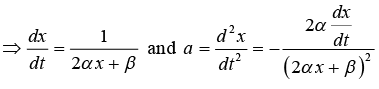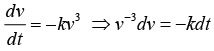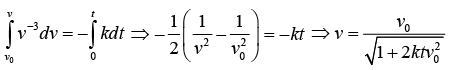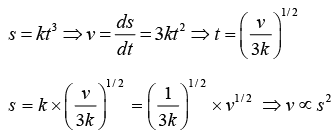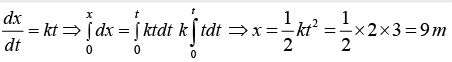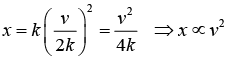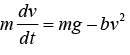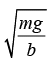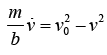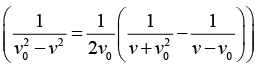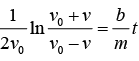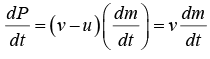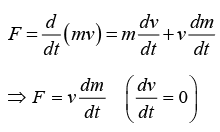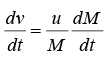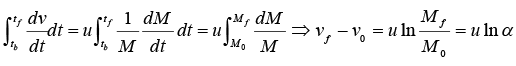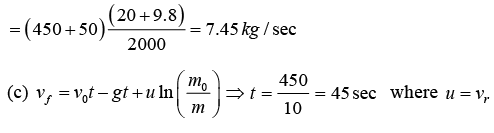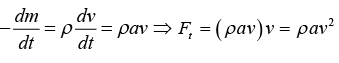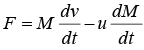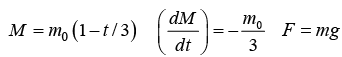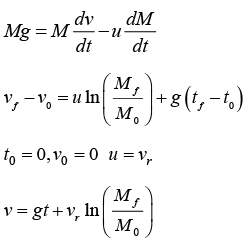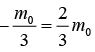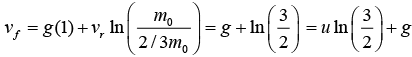Equations of Motion & Variable Mass | Mechanics & General Properties of Matter - Physics PDF Download
Equation of Motion
According to Newton’s law of motion Force acting on a body F = ma
where acceleration α is given by α = 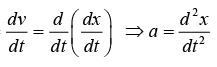
If velocity is only function of position One can also represent acceleration as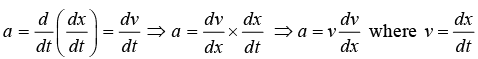
to be used when v is a function of x only and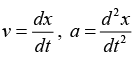
Example 1: An object moving with a speed of 6.25 m /s is decelerated at a rate given by dv/dt = k√v where k = 2.5 and v is the instantaneous speed. Find the time taken by the object to come to rest
Integrating =(at t = 0,v = 6.25m/s , at t = t, v = 0)
Putting k = 2.5 , t = 2 sec
Example 2: Time and distance of an object are related as t = αx2 + βx , here α and β are constants. The retardation is given by kvn. Find the values of k and n.
t = αx2 + βx
Differentiating wrt t , dt/dt = α x
⇒ α = -2αv × v2 = -2αv3. So k = -2α, n = 3
Example 3: The acceleration experienced by a boat after the engine is cut off, is given by dv/dt = -kv3, k is a constant. If v0 is the magnitude of velocity at cut off, find the velocity after time t from cut off.
Example 4: Displacement of a body is given by s ∝ t3, t is the time elapsed
(a) Find the relation between velocity v and displacement s
(b) Find the relation between acceleration α and displacement s
(a) As s = kt3
(b) s = kt3 ⇒ v = ds/dt = 3k and acceleration α = dv/dt ⇒ α = 6kt ⇒ t = α/6k
Example 5: A particle starts from rest moves with a velocity given by v = kt (here k = 2m/s2)
(a) Find the distance covered by the particle in first 3 sec.
(b) Draw distance versus time x - t , x - v and x - a graphs
(a)
(b) x ∝ t2 x = kt2v = ds/dt = 2kt
α = dv/dt = 2k ⇒ α = 2k x x0
α ∝ x0 (α is constant)
Example 6: We want to find the velocity of a falling parachutist as a function of time and are particularly interested in the constant limiting velocity, v0, that comes about by air drag, taken to be quadratic, -bv2 and opposing the force of the gravitational attraction, mg, of the Earth on the parachutist. We choose a coordinate system in which the positive direction is downward so that the gravitational force is positive. For simplicity we assume that the parachute opens immediately, that is, at time t = 0 , where v (t) = 0 , our initial condition.
(a) Write down equation of motion
(b) Find terminal velocity v0
(c) if v0 is terminal velocity then find the velocity after time t
(a)
where m includes the mass of the parachute.
(b) The terminal velocity, v0 can be found from the equation of motion as t → ∞, when there is no acceleration, v = 0 ⇒ bv02 = mg or v0 =
(c) It simplifies further work to rewrite equation (i) as
This equation is separable and we write it in the form...(2) Using partial fractions to write
It is straightforward to integrate both sides of equation (2) (the left-hand side from v = 0 to v, the right-hand side from t = 0 to t ), yielding
Solving for the velocity, we have
where T =is the time constant governing the asymptotic approach of the velocity to its limiting value, v0.
Variable Mass and Momentum
Case 1-Motion of Spacecraft
A spacecraft moves through space with constant velocity v . The space craft encounters a stream of dust particles which embed themselves in it at rate dm/dt . The dust has velocity u just before it hits. At time t the total mass of the spacecraft is M (t). The problem is to find external force F necessary to keep the spacecraft moving uniformly. (In practice F would most likely come from the spacecraft’s own rocket engines. For simplicity, we can visualize the source F to be completely external - an invisible hand, so to speak.)
Let us focus on the short time interval between t and t + Δt . The drawings below show the system at the beginning and end of the interval.
 Time t , mass of system =M (t)+ Δm
Time t , mass of system =M (t)+ Δm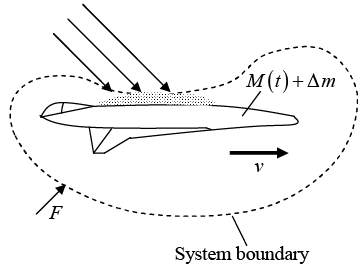 Time t +Δt, mass of system = M (t) +Δm
Time t +Δt, mass of system = M (t) +Δm
Let Δm denote the mass added to the satellite during Δt . The system consist of masses are M (t) and Δm.
The initial momentum is P (t) = M (t) v+ (Δm) u.
The final momentum is P (t + Δt) - P (t) = ( v - u )Δm. The rate of change of momentum is approximately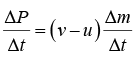
In the limit Δt → 0, we have the exact result 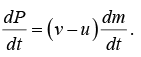
Since F = dP/dt , the required external force is F = (v - u) dm/dt.
Note that F can be either positive or negative depending on the direction of the stream of mass.
If u = v, the momentum of the system is constant, and F = 0.
Example 7: Sand falls from a stationary hopper onto a freight car which is moving with uniform velocity v. The sand falls at the rate dm/dt. How much forces needed to keep the freight car moving a the speed v?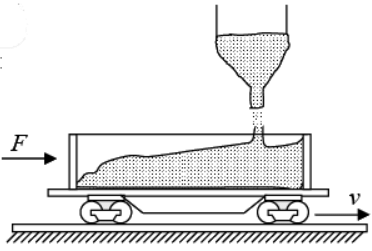
In this case, the initial speed of the sand is 0 , and
The required force isWe can understand why this force is needed by considering in detail just what happens to a sand grain as it lands on the surface of the freight car.
Example 8: A truck is moving at a speed of 20 m / sec , sand is poured into it at a rate of 2 kg / sec , then find the thrust force acting on it.
If m0 is initial mass of sand with truck,
Pi = m0 + μtv0
Pf = ((m0 + μt) + μdt) v0
F = dp/dt = μv0 = 2 x 20 = 40N
Example 9: A truck is moving at a speed of 20 m/sec . If sand leaks at the rate of 2 kg/sec from the truck at the same time, find the thrust force.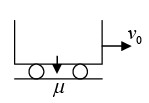
Pi = m0v0 - µtv0
Pf = (m0 - μ(t + dt))v0 + µdtv0 + µdtv0
ΔP = Pf - Pi = 0
Ft = dp/dt = 0N
Example 10: If Sand is poured at 2 kg / sec and leaks at same rate while truck moves at 20 m/sec , find the thrust force.
Pi = m0v0 + µ dtv0
Pf = m0 - µdt)v0 + µdtv0 + µdtv0
Pf - Pi = µdtv0= 2 x 20 = 40N
As sand has zero velocity in horizontal direction when it first comes out of truck.
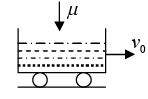
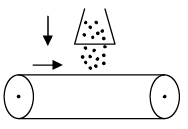
A conveyor belt moving with a mass like sand (from a stationary hopper) falling on it continuously
A conveyor belt moves with a velocity v (as shown in figure). Sand falls on it from a stationary hopper at a rate of mkg / sec . As the sand comes in contact with belt, it aquires the velocity of belt but due to inertia, it tries to move in opposite direction.
The force acting on the belt is
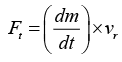
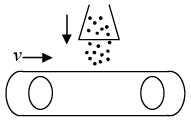
This is in the direction opposite to motion of the belt as dm/dt > 0 .
Due to this an additional power P = Ft × v is to be provided to keep belt moving at same speed. Friction, if present, also needs extra power to be applied at motor.
Example 11: A conveyor belt is moving at a speed of 0.75 m / sec and sand is falling on it at a rate of 5 kg / sec.
(a) Find the rate of change of sand
(b) Find the force applied by belt of the sand
(c) If belt moves with constant velocity and force is constant, what is work done?
(d) Find the rate of increase of kinetic energy.
(e) Why change (increase) in K.E. is not equal to work done, where does the difference go?
(a) Rate of change of momentum is equal to external force applied,
The initial momentum of sand in direction of moment of belt is zero and as soon as it comes in contact with belt, the momentum of sand is same as that of belt, if there is no friction.
So, F = 0.75× 5 = 3.75N
(b) F = 3.75N is the force applied by belt on sand in forward direction.
(c) W = Fvt = 3.85 × 0.75 × 1 = 2.85 J
(d) K.E. = 1/2 v2(dm/dt) t = 1/2 x 0.75 x 0.75 x 5 x 1 = 1.41 J (t = 1sec)
(e) K.E. = 2.85 - 1.41 = 1.44 J
This difference of energy is lost in doing work against friction.
 |
Download the notes
Equations of Motion & Variable Mass
|
Download as PDF |
Case -2 Motion of Rocket
The concept of momentum is invaluable in understanding the motion of a rocket. A rocket accelerates by expelling gas at a high velocity; the reaction force of the gas on the rocket accelerates the rocket in the opposite direction. The mechanism is illustrated by the drawings of the cubical chamber containing gas at high pressure
 Force on chamber
Force on chamber
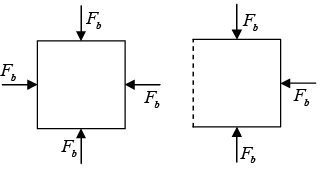 Force on gasThe gas presses outward on each wall with the force Fa (We show only four walls for clarity.) The vector sum of the Fa's is zero, giving zero net force on the chamber. Similarly each wall of the chamber exerts a force on the gas Fb = -Fa; the net force on the gas is also zero. In the right hand drawings below, one wall has been removed. The net force on the chamber is Fa, to the right. The net force on the gas is Fb, to the left. Hence, the gas accelerates to the left, and the chamber accelerates to the right. To analyze the motion of the rocket in detail, we must equate the external force on the system, F , with the rate of change of momentum, dP/dt . Consider the rocket at time t . Between t and t + Δt a mass of fuel Δm is burned and expelled as gas with velocity u relative to the rocket. The exhaust velocity u is determined by the nature of the propellants, the throttling of the engine, etc., but it is independent of the velocity of the rocket.
Force on gasThe gas presses outward on each wall with the force Fa (We show only four walls for clarity.) The vector sum of the Fa's is zero, giving zero net force on the chamber. Similarly each wall of the chamber exerts a force on the gas Fb = -Fa; the net force on the gas is also zero. In the right hand drawings below, one wall has been removed. The net force on the chamber is Fa, to the right. The net force on the gas is Fb, to the left. Hence, the gas accelerates to the left, and the chamber accelerates to the right. To analyze the motion of the rocket in detail, we must equate the external force on the system, F , with the rate of change of momentum, dP/dt . Consider the rocket at time t . Between t and t + Δt a mass of fuel Δm is burned and expelled as gas with velocity u relative to the rocket. The exhaust velocity u is determined by the nature of the propellants, the throttling of the engine, etc., but it is independent of the velocity of the rocket.
The sketches below show the system at time t and at time t + Δt . The system consists of Δm plus the remaining mass of the rocket M . Hence the total mass is M + Δm.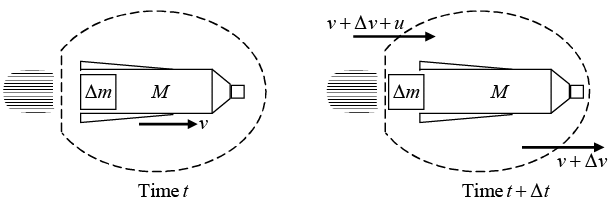 The velocity of the rocket at time t is v (t) , and at t + Δt it is v + Δv .
The velocity of the rocket at time t is v (t) , and at t + Δt it is v + Δv .
The initial momentum is P (t ) = ( M+ Δm) v
The final momentum is P (t + Δt ) = M ( v + Δv ) + Δm (v + Δv + u) The change in momentum is ΔP = P (t + Δt) Δ P (t) = M Δv + (Δm) u assume Δm.Δv = 0
Therefore, 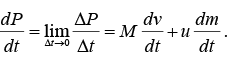
Note that we have defined u to be positive in the direction of v . In most rocket applications, u is negative, opposite to v . It is inconvenient to have both m and M in the equation. dm/dt is the rate of increase of the exhaust mass. Since, this mass comes from the rocket,
dm/dt = - DM/dt
equating the external force to dP/dt , we obtain the fundamental rocket equation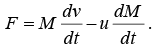
It may be useful to point out two minor subtleties in our development. The first is that the velocities have been expressed with respect to an inertial frame, not a frame attached to the rocket. The second is that we took the final velocity of the element exhaust gas to be v + Δv + u rather than v + u.
Example 12: (a) A rocket is moving vertically in absence of gravity .if initial exhaust speed and mass of rocket is u and M0 respectively. What will be speed if mass became αM0 after time t = tf. (assume t = 0 velocity of rocket is v0.)
(b) How situation will different if a gravitational field is present.
(a) If there is no external force on a rocket, F = 0 and its motion is given by
or
Generally the exhaust velocity is constant. In this case it is easy to integrate the equation of motion.
(b) If a rocket takes off in a constant gravitational field,where u and g are directed down and are assumed to be constant.
integrating with respect to time, we obtain
+ g (tf - t0) ⇒vf = v0 + u In (a) + gtf.
Example 13: A rocket set for vertical firing, weighs 50 kg and contains 450 kg fuel. It can have a maximum exhaust weight of 2 km/ sec . Find minimum rate of fuel consumption
(a) to just lift it off
(b) to give it an acceleration of 20 m / sec2
(c) What will be the speed of rocket when rate of consumption of fuel is 10 kg / s after whole of the fuel is consumed?
(a) For just lifting it off, W = Ft (Thrust force)
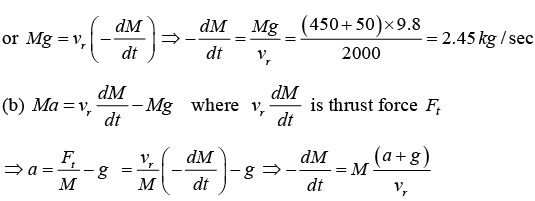
Thrust Applied by a Fluid Coming Out of a Container Kept on a Surface.
Water has change in it’s momentum and hence it leads to a thrust for acting on tank as dm/dt < 0
So, Ft = dm/dt x v ⇒Ft = (ραv) x v = ραv2
here α is cross section area of the water efflux and ρ is it’s density.
Example 14: A liquid of density ρ is filled in a tank which has a value at depth h from free surface. The liquid comes out with a speed v.
(a) Find the thrust force acting on the tank
(b) If the value of h is 19.6 m and a = 1cm2, α = 1000 kg / m3, find the thrust force.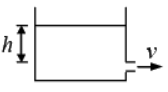
(a)
(α is cross section area of opening)
vr = v
(b) As v =19.6m/sec
Example 15: A rocket of initial mass m0(1 - t/3) at time t. The rocket is launched from rest vertically upward under gravity and experts burnt fuel at a speed vr relative to the rocket vertically downward. Find the speed of rocket at t = 1 .
At t = 1, mass will remain, Mf = m0 =
Now using the equation,
Motion of uniform chain vertically on a horizontal surface
A chain of constant mass density λ = m/l, moving down with velocity v experiences a thrust force on it given by 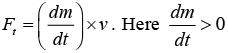 and the chain does not form a heap, so thrust opposes the motion of chain.
and the chain does not form a heap, so thrust opposes the motion of chain.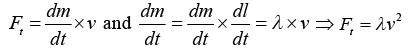
Example 16: A uniform chain of mass m and length l hangs on a thread and touches the surface of a table by its lower end. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap.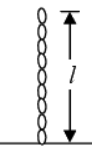
Force exerted by the chain on the table. It consists of two parts:
(a) Weight of the portion BC of the chain lying on the table,
w = mg/2 (downward)
(b) Thrust force Ft = λv2
Here, λ = mass per unit length of chain m/l(downward)
∴ Net force exerted by the chain on the table is
F = W + Ft = mg/2 + mg = 3/2 mg
So, from Newton’s third law the force exerted by the table on the chain will be
3/2 mg (vertically upward)
|
61 videos|23 docs|25 tests
|
FAQs on Equations of Motion & Variable Mass - Mechanics & General Properties of Matter - Physics
| 1. What are the equations of motion for variable mass systems? |  |
| 2. How are the equations of motion modified for variable mass systems? |  |
| 3. What is the principle behind the equations of motion for variable mass systems? |  |
| 4. How are the equations of motion for variable mass systems useful in real-life scenarios? |  |
| 5. Can the equations of motion for variable mass systems be applied to everyday objects? |  |