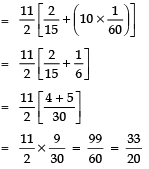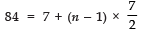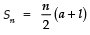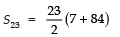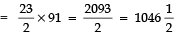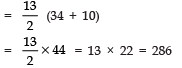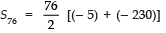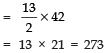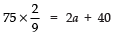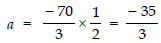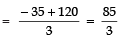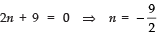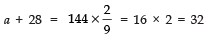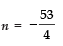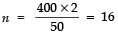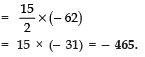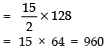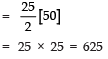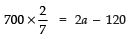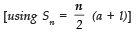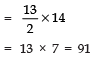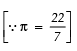NCERT Solutions for Class 10 Maths Chapter 5 - Arithmetic Progressions (Exercise 5.2)
Exercise 5.3
 Formula for Sum of an AP
Formula for Sum of an AP
Q1: Find the sum of the following APs:
(i) 2, 7, 12, ..., to 10 terms.
Here, a = 2
d = 7 - 2 = 5
n = 10
Since, Sn = n/2 [2a + (n - 1) d]
∴ S10 = [2 × 2 + (10 - 1) × 5]
⇒ S10 = 5 [4 + 9 × 5]
⇒ S10 = 5 [49] = 245
Thus, the sum of first 10 terms is 245.
(ii) - 37, - 33, - 29, ..., to 12 terms.
We have:
a = - 37
d = - 33 - (- 37) = 4
n = 12
∴ Sn = n/2 [2a + (n - 1) d]
⇒ S12 = 12/2 [2 (- 37) + (12 - 1) × 4]
= 6 [- 74 + 11 × 4]
= 6 [- 74 + 44]
= 6 × [- 30] = - 180
Thus, sum of first 12 terms = -180.
(iii) 0.6, 1.7, 2.8, ..., to 100 terms.
Here, a = 0.6
d = 1.7 - 0.6 = 1.1
n = 100
∴ Sn = n/2 [2a + (n - 1) d]
S100 = 100/2 [2 (0.6) + (100 - 1) × 1.1]
= 50 [1.2 + 99 × 1.1]
= 50 [1.2 + 108.9]
= 50 [110.1]
= 5505
Thus, the required sum of first 100 terms is 5505.
(iv) Solve the following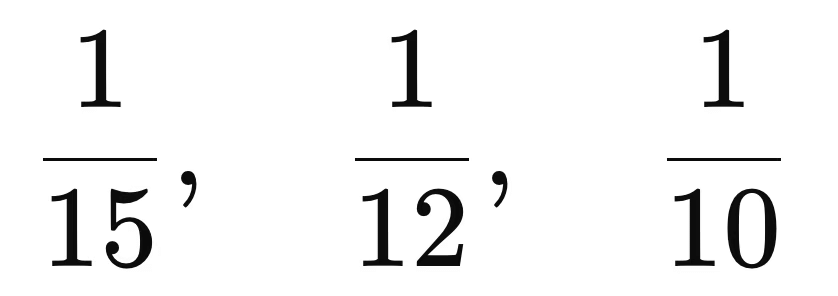 , ..., to 11 terms.
, ..., to 11 terms.
Here,
a = 1/15
d =
n = 11
∴ Sn = n/2 [2a + (n - 1) d]
S11 =
Thus, the required sum of first 11 terms = 33/20.
Q2: Find the sums given below:
(i)
Here, a = 7
l = 84
Let n be the number of terms
∴ Tn = a + (n - 1) d
⇒
⇒
⇒ n = 22 + 1 = 23
Now,
⇒
Thus, the required sum =
(ii) 34 + 32 + 30 + ... + 10
Here, a = 34
d = 32 - 34 = - 2
l = 10
Let the number of terms be n
∴ Tn = 10
Now Tn = a + (n - 1) d
⇒ 10 = 34 + (n - 1) × (- 2)
⇒ (n - 1) × (- 2) = 10 - 34 = - 24
⇒
⇒ n = 13⇒
Now,
⇒
=
=
=
= 13 × 22 = 286
OR
S13 = n/2 (a + l)
Thus, the required sum is 286.
(iii) - 5 + (- 8) + (- 11) + ... + (- 230)
Here, a = - 5
d = - 8 - (- 5) = - 3
l = - 230
Let n be the number of terms.
∴ Tn = - 230
⇒ - 230 = - 5 + (n - 1) × (- 3)
⇒ (n - 1) × (- 3) = - 230 + 5 = - 225
⇒ n - 1 = -225/-3 = 75
⇒ n = 75 + 1 = 76
Now,
= 38 × (- 235)
= - 8930
∴ The required sum = - 8930.
Q3: In an AP:
(i) given a = 5, d = 3, an = 50, find n and Sn.
Here, a = 5, d = 3 and an = 50 = l
∵ an = a + (n - 1) d
∴ 50 = 5 + (n - 1) × 3
⇒ 50 - 5 = (n - 1) × 3
⇒ (n - 1) × 3 = 45
⇒ (n - 1) = 45/3 =15
⇒ n = 15 + 1 = 16
Now Sn = n/2 (a + l)
= 16/2 (5 + 50)
= 8 (55) = 440
Thus, n = 16 and Sn = 440
(ii) given a = 7, a13 = 35, find d and S13.
(ii) Here, a = 7 and a13 = 35 = l
∴ an = a + (n - 1) d
⇒ 35 = 7 + (13 - 1) d
⇒ 35 - 7 = 12d
⇒ 28 = 12d
⇒ d = 28/12 = 7/3
Now, using
Sn = n/2 (a + l)
S13 = 13/2 (7 + 35)
Sn = 273 and d = 7/3
(iii) given a12 = 37, d = 3, find a and S12.
Here, a12 = 37 = l and d = 3
Let the first term of the AP be ‘a’.
Now a12 = a + (12 - 1) d
⇒ 37 = a + 11d
⇒ 37 = a + 11 × 3
⇒ 37 = a + 33
⇒ a = 37 - 33 = 4
Now, Sn = n/2 (a + l)
⇒ S12 = 12/2 (4 + 37)
⇒ S12 = 6 × (41) = 246
Thus, a = 4 and S12 = 246
(iv) given a3 = 15, S10 = 125, find d and a10.
Here, a3 = 15 = l
S10 = 125
Let first term of the AP be ‘a’ and the common difference = d
∴ a3 = a + 2d
⇒ a + 2d = 15 ...(1)
Again Sn = n/2 [2a + (n - 1) d]
⇒ S10 = 10/2 [2a + (10 - 1) d]
⇒ 125 = 5 [2a + 9d]
⇒ 2a + 9d = 125/5 = 25
⇒ 2a + 9d = 25 ...(2)
Multiplying (1) by 2 and subtracting (2) from it, we get
2 [a + 2d = 15] - [2a + 9d = 25]
⇒ 2a + 4d - 2a - 9d = 30 - 25
⇒ - 5d = 5
⇒ d =5/-5 = -1
∴ From (1), a + 2 (- 1) = 15 ⇒ a = 15 + 2 ⇒ a = 17
Now, a10 = a + (10 - 1) d
= 17 + 9 × (- 1)
= 17 - 9 = 8
Thus, d = - 1 and a10 = 8
(v) given d = 5, S9 = 75, find a and a9.
Here, d = 5, S9 = 75
Let the first term of the AP is ‘a’.
∴ S9 = 9/2 [2a + (9 - 1) × 5]
⇒ 75 = 9/2 [2a + 40]
⇒
⇒ 50/3 = 2a + 40
⇒
⇒
Now, a9 = a + (9 - 1) d
=
=
Thus,
(vi) given a = 2, d = 8, Sn = 90, find n and an.
Here, a = 2, d = 8 and Sn = 90
∵ Sn = n/2 [2a + (n - 1) d]
∴ 90 = n/2 [2 × 2 + (n - 1) × 8]
⇒ 90 × 2 = 4n + n (n - 1) × 8
⇒ 180 = 4n + 8n2 - 8n
⇒ 180 = 8n2 - 4n
⇒ 45 = 2n2 - n
⇒ 2n2 - n - 45 = 0
⇒ 2n2 - 10n + 9n - 45 = 0
⇒ 2n (n - 5) + 9 (n - 5) = 0
⇒ (2n + 9) (n - 5) = 0
∴ Either
or n - 5 = 0 ⇒ n = 5
Butis not required. ∴n = 5
Now, an = a + (n - 1) d
⇒ a5 = 2 + (5 - 1) × 8
= 2 + 32 = 34
Thus, n = 5 and a5 = 34.
(vii) given a = 8, an = 62, Sn = 210, find n and d.
Here, a = 8, an = 62 = l and Sn = 210
Let the common difference = d
Now, Sn = 210
⇒ 210 = n/2 (a + l)
⇒ 210 = n/2 (8 + 62) =
∴ n = 210/35 = 6
Again an = a + (n - 1) d
⇒ 62 = 8 + (6 - 1) × d
⇒ 62 - 8 = 5d
⇒ 54 = 5d ⇒ d = 54/5
Thus, n = 6 and d = 54/5 .
(viii) given an = 4, d = 2, Sn = - 14, find n and a.
Here, an = 4, d = 2 and Sn = - 14
Let the first term be ‘a’.
∵ an = 4
∴ a + (n - 1) 2 = 4
⇒ a + 2n - 2 = 4
⇒ a = 4 - 2n + 2
⇒ a = 6 - 2n ...(1)
Also Sn = - 14
⇒ n/2 (a + l) = - 14
⇒ n/2 (a + 4) = - 14
⇒ n (a + 4) = - 28 ...(2)
Substituting the value of a from (1) into (2),
n [6 - 2n + 4] = - 28
⇒ n [10 - 2n] = - 28
⇒ 2n [5 - n] = - 28
⇒ n (5 - n) = - 14 [Dividing throughout by 2]
⇒ 5n - n2 + 14 = 0
⇒ n2 - 5n - 14 = 0
⇒ n2 - 7n + 2n - 14 = 0
⇒ n (n - 7) + 2 (n - 7) = 0
⇒ (n - 7) (n + 2) = 0
∴ Either n - 7 = 0 ⇒ n = 7
or n + 2 = 0 ⇒ n = - 2
But n cannot be negative,
∴ n = 7
Now, from (1), we have
a = 6 - 2 × 7 ⇒ a = - 8
Thus, a = - 8 and n = 7
(ix) given a = 3, n = 8, S = 192, find d.
Here, a = 3, n = 8 and Sn = 192
Let the common difference = d.
∵ Sn = n/2 [2a + (n - 1) d]
∴ 192 = 8/2 [2 (3) + (8 - 1) d]
⇒ 192 = 4 [6 + 7d]
⇒ 192 = 24 + 28d
⇒ 28d = 192 - 24 = 168
⇒ d = 168/28 =6
Thus, d = 6.
(x) given l = 28, S = 144, and there are total 9 terms. Find a.
(x) Here, l = 28 and S9 = 144
Let the first term be ‘a’.
Then Sn = n/2 (a + l)
⇒ S9 = 9/2 (a + 28)
⇒ 144 = 9/2 (a + 28)
⇒
⇒ a = 32 - 28 = 4
Thus, a = 4.
Q4: How many terms of the AP: 9, 17, 25, ... must be taken to give a sum of 636?
Here, a = 9
d = 17 - 9 = 8
Sn = 636
∵ Sn = n/2 [2a + (n - 1) d] = 636
∴ n/2 [(2 × 9) + (n - 1) × 8] = 636
⇒ n [18 + (n - 1) × 8] = 1272
⇒ n (8n + 10) = 1272
⇒ 8n2 + 10n - 1272 = 0
⇒ 4n2 + 5n - 636 = 0
⇒ 4n2 + 53n - 48n - 636 = 0
⇒ n (4n + 53) - 12 (4n + 53) = 0
⇒ (n - 12) (4n + 53) = 0
⇒ n = 12 and
Rejecting, we have n = 12.
Q5: The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Here, a = 5
l = 45 = Tn
Sn = 400
∵ Tn = a + (n - 1) d
∴ 45 = 5 + (n - 1) d
⇒ (n - 1) d = 45 – 5
⇒ (n - 1) d = 40 ...(1)
Also Sn = n/2 (a + l)
⇒ 400 = n/2 (5 + 45)
⇒ 400 × 2 = n × 50
⇒
From (1), we get
(16 - 1) d = 40
⇒ 15d = 40
⇒ d = 40/15 = 8/3
Q6: The first and the last terms of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum
We have,
First term a = 17
Last term l = 350 = Tn
Common difference d = 9
Let the number of terms be ‘n’
∵ Tn = a + (n - 1) d
∴ 350 = 17 + (n - 1) × 9
⇒ (n - 1) × 9 = 350 - 17 = 333
⇒ n - 1 = 333/9 = 37
⇒ n = 37 + 1 = 38
Since, Sn = n/2 (a + l)
∴ S38 = 38/2 (17 + 350)
= 19 (367) = 6973
Thus, n = 38 and Sn = 6973
Q7: Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149.
Here, n = 22, T22 = 149 = l
d = 7
Let the first term of the A.P. be ‘a’.
∴ Tn = a + (n - 1) d
⇒ Tn = a + (22 - 1) × 7
⇒ a + 21 × 7 = 149
⇒ a + 147 = 149
⇒ a = 149 - 147 = 2
Now, S22 = n/2 [a + l]
⇒ S22 = 22/2 [2 + 149]
= 11 [151] = 1661
Thus S22 = 1661
Q8: Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
Here, n = 51, T2 = 14 and T3 = 18
Let the first term of the A.P. be ‘a’ and the common difference is d.
∴We have:
T2 = a + d ⇒ a + d = 14 ...(1)
T3 = a + 2d ⇒ a + 2d = 18 ...(2)
Subtracting (1) from 2, we get
a + 2d - a - d = 18 - 14
⇒ d = 14
From (1), we get
a + d = 14 ⇒ a + 4 = 14
⇒ a = 14 - 4 = 10
Now, Sn = n/2 [2a + (n - 1) d]
⇒ S51 = 51/2 [(2 × 10) + (51 - 1) × 4]
= 51/2 [20 + 200]
= 51/2 [220]
= 51 × 110 = 5610
Thus, the sum of 51 terms is 5610.
Q9: If the sum of first 7 terms of an A.P. is 49 and that of 17 terms is 289, find the sum of first n terms.
Here, we have:
S7 = 49 and S17 = 289
Let the first term of the A.P. be ‘a’ and ‘d’ be the common difference, then
Sn = n/2 [2a + (n - 1) d]
⇒ S7 = 7/2 [2a + (7 - 1) d] = 49
⇒ 7 (2a + 6d) = 2 × 49 = 98
⇒ 2a + 6d = 98/7 = 14
⇒ 2 [a + 3d] = 14
⇒ a + 3d = 14/2 = 7
⇒ a + 3d = 7 ...(1)
Also, S17 = 17/2[2a + (17 - 1) d] = 289
⇒ 17/2 (2a + 16d) = 289
⇒ a + 8d = 289/17 = 17
⇒ a + 8d = 17 ...(2)
Subtracting (1) from (2), we have:
a + 8d - a - 3d = 17 - 7
⇒ 5d = 10
⇒ d =10/5 = 2
Now, from (1), we have
a + 3 (2) = 7
⇒ a = 7 - 6 = 1
Now, Sn = n/2 [2a + (n - 1) d]
= n/2 [2 × 1 + (n - 1) × 2]
= n/2 [2 + 2n - 2]
= n/2 [2n]
= n × n = n2
Thus, the required sum of n terms = n2.
Q10: Show that a1, a2, ..., an, ... form an A.P. where an is defined as below:
(i) an = 3 + 4n
(ii) an = 9 - 5n
Also find the sum of the first 15 terms in each case.
(i) Here, an = 3 + 4n
Putting n = 1, 2, 3, 4, ..... n, we get:
a1 = 3 + 4 (1) = 7
a2 = 3 + 4 (2) = 11
a3 = 3 + 4 (3) = 15
a4 = 3 + 4 (4) = 19
..... ..... .....
an = 3 + 4n
∴ The A.P. in which a = 7 and d = 11 - 7 = 4 is:
7, 11, 15, 19, ....., (3 + 4n).
Now S15 = 15/2 [(2 × 7) + (15 - 1) × 4]
= 15/2 [14 + (14 × 4)]
= 15/2 [14 + 56]
= 15/2[70]
= 15 × 35 = 525
(ii) Here, an = 9 - 5n
Putting n = 1, 2, 3, 4, ....., n, we get
a1 = 9 - 5 (1) = 4
a2 = 9 - 5 (2) = - 1
a3 = 9 - 5 (3) = - 6
a4 = 9 - 5 (4) = - 11
..... .....
∴ The A.P. is:
4, - 1, - 6, - 11, ..... 9 - 5 (n) [having first term as 4 and d = - 1 - 4 = - 5]
∴ S15 = 15/2 [(2 × 4) + (15 - 1) × ( - 5)]
= 15/2[8 + 14 × (- 5)]
= 15/2[8 - 70]
Q11: If the sum of the first n terms of an AP is 4n - n2, what is the first term (that is S1)? What is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and the nth terms.
We have:
Sn = 4n - n2
∴ S1 = 4 (1) - (1)2
= 4 - 1 = 3 ⇒ First term = 3
S2 = 4 (2) - (2)2
= 8 - 4 = 4 ⇒ Sum of first two terms = 4
∴ Second term (S2 - S1) = 4 - 3 = 1
S3 = 4 (3) - (3)2
= 12 - 9 = 3 ⇒ Sum of first 3 terms = 3
∴ Third term (S3 - S2) = 3 - 4 = - 1
S9 = 4 (9) - (9)2
= 36 - 81 = - 45
S10 = 4 (10) - (10)2
= 40 - 100 = - 60
∴ Tenth term = S10 - S9 = [- 60] - [- 45] = - 15
Now, Sn = 4 (n) - (n)2 = 4n - n2
Also Sn - 1 = 4 (n - 1) - (n - 1)2
= 4n - 4 - [n2 - 2n + 1]
= 4n - 4 - n2 + 2n - 1
= 6n - n2 - 5
∴ nth term = Sn - Sn - 1
= [4n - n2] - [6n - n2 - 5]
= 4n - n2 - 6n + n2 + 5 = 5 - 2n
Thus,
S1 = 3 and a1 = 3
S2 = 4 and a2 = 1
S3 = 3 and a3 = - 1
a10 = - 15 and an = 5 - 2n
Q12: Find the sum of the first 40 positive integers divisible by 6.
The first 40 positive integers divisible by 6 are:
6, 12, 18, ....., (6 × 40).
And, these numbers are in A.P. such that
a = 6
d = 12 - 6 = 6 and an = 6 × 40 = 240 = l
∴ S40 = 40/2 [(2 × 6) + (40 - 1) × 6]
= 20 [12 + 39 × 6]
= 20 [12 + 234]
= 20 × 246 = 4920
OR
Sn = n/2 [a + l]
S40 = 40/2[6 + 240]
= 20 × 246 = 4920
Thus, the sum of first 40 multiples of 6 is 4920.
Q13: Find the sum of the first 15 multiples of 8.
The first 15 multiples of 8 are:
8, (8 × 2), (8 × 3), (8 × 4), ....., (8 × 15)
or 8, 16, 24, 32, ....., 120.
These numbers are in A.P., where
a = 8 and l = 120
∴ S15 = 15/2 [a + l]
= 15/2 [8 + 120]
Thus, the sum of first positive 15 multiples of 8 is 960.
Q14: Find the sum of the odd numbers between 0 and 50.
Odd numbers between 0 and 50 are:
1, 3, 5, 7, ....., 49
These numbers are in A.P. such that
a = 1 and l = 49
Here, d = 3 - 1 = 2
∴ Tn = a + (n - 1) d
⇒ 49 = 1 + (n - 1) 2
⇒ 49 - 1 = (n - 1) 2
⇒ (n - 1) = 48/2 = 24
∴ n = 24 + 1 = 25
Now, S25 = 25/2[1+49]
Thus, the sum of odd numbers between 0 and 50 is 625.
Q15: A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: ₹ 200 for the first day, ₹ 250 for the second day, ₹ 300 for the third day, etc., the penalty for each succeeding day being ₹ 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days?
Here, penalty for delay on
1st day = ₹ 200
2nd day = ₹ 250
3rd day = ₹ 300
...............
...............
Now, 200, 250, 300, ..... are in A.P. such that
a = 200, d = 250 - 200 = 50
∴ S30 is given by
S30 = 30/2 [2 (200) + (30 - 1) × 50]
= 15 [400 + 29 × 50]
= 15 [400 + 1450]
= 15 × 1850 = 27,750
Thus, penalty for the delay for 30 days is ₹ 27,750.
Q16: A sum of ₹ 700 is to be used to give seven cash prizes to students of a school for their overall academic performace. If each prize is ₹ 20 less than its preceding prize, find the value of each of the prizes.
Sum of all the prizes = ₹ 700
Let the first prize = a
∴ 2nd prize = (a - 20)
3rd prize = (a - 40)
4th prize = (a - 60)
........................................
Thus, we have, first term = a
Common difference = - 20
Number of prizes, n = 7
Sum of 7 terms Sn = 700
Since, Sn = n/2 [2a + (n - 1) d]
⇒ 700 = 7/2 [2 (a) + (7 - 1) × (- 20)]
⇒ 700 = 7/2 [2a + (6 × - 20)]
⇒
⇒ 200 = 2a - 120
⇒ 2a = 200 + 120 = 320
⇒ a = 320/2 = 160
Thus, the values of the seven prizes are:
₹ 160, ₹ (160 - 20), ₹ (160 - 40), ₹ (160 - 60), ₹ (160 - 80), ₹ (160 - 100) and
₹ (160 - 120)
⇒ ₹ 160, ₹ 140, ₹ 120, ₹ 100, ₹ 80, ₹ 60 and ₹ 40.
Q17: In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
Number of classes = 12
∵ Each class has 3 sections.
∴ Number of plants planted by class I = 1 × 3 = 3
Number of plants planted by class II = 2 × 3 = 6
Number of plants planted by class III = 3 × 3 = 9
Number of plants planted by class IV = 4 × 3 = 12
.......................................................................................................
Number of plants planted by class XII = 12 × 3 = 36
The numbers 3, 6, 9, 12, ..........., 36 are in A.P.
Here, a = 3 and d = 6 - 3 = 3∵ Number of classes = 12
i.e., n = 12
∴ Sum of the n terms of the above A.P., is given by
S12 = 12/2 [2 (3) + (12 - 1) 3]
= 6 [6 + 11 × 3]
= 6 [6 + 33]
= 6 × 39 = 234
Thus, the total number of trees = 234.
Q18: A spiral is made up of successive semi-circles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, ..... as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semi-circles? (Take π =22/7)
[Hint: Length of successive semi-circles is l1, l2, l3, l4, ... with centres at A, B, A, B, ..., respectively.]
Length of a semi-circle = semi-circumference
= 1/2 (2πr)
= πr
∴ l1 = π r1 = 0.5 π cm = 1 × 0.5 π cm
l2 = π r2 = 1.0 π cm = 2 × 0.5 π cm
l3 = π r3 = 1.5 π cm = 3 × 0.5 π cm
l4 = π r4 = 2.0 π cm = 4 × 0.5 π cm
...... ............... ......................
l13 = π r13 cm = 6.5 π cm = 13 × 0.5 π cm
Now, length of the spiral
= l1 + l2 + l3 + l4 + ..... + l13
= 0.5 π [1 + 2 + 3 + 4 + ..... + 13] cm ...(1)
∵ 1, 2, 3, 4, ....., 13 are in A.P. such that
a = 1 and l = 13
∴ S13 = 13/2 [1+13]
∴ From (1), we have:
Total length of the spiral
= 1.5 π [91] cm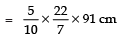
Q19: 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (see figure). In how many rows are the 200 logs placed and how many logs are in the top row?
We have:
The number of logs:
1st row = 20
2nd row = 19
3rd row = 18
obviously, the numbers
20, 19, 18, ....., are in A.P. such that
a = 20
d = 19 - 20 = - 1
Let the numbers of rows be n.
∴ Sn = 200
Now, using, Sn = [2a + (n - 1) d], we get
Sn = n/2 [2 (20) + (n - 1) × (- 1)]
⇒ 200 = n/2 [40 - (n - 1)]
⇒ 2 × 200 = n × 40 - n (n - 1)
⇒ 400 = 40n - n2 + n
⇒ n2 - 41n + 400 = 0
⇒ n2 - 16n - 25n + 400 = 0
⇒ n (n - 16) - 25 (n - 16) = 0
⇒ (n - 16) (n - 25) = 0
Either
⇒ n - 16 = 0 ⇒ n = 16
or n - 25 = 0 ⇒ n = 25
Tn = 0 ⇒ a + (n - 1) d = 0 ⇒ 20 + (n - 1) × (- 1) = 0
⇒ n - 1 = 20 ⇒ n = 21
i.e., 21st term becomes 0
∴ n = 25 is not required.
Thus, n = 16
∴ Number of rows = 16
Now, T16 = a + (16 - 1) d
= 20 + 15 × (- 1)
= 20 - 15 = 5
∴ Number of logs in the 16th (top) row is 5.
Q20: In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line.

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
[Hint: To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is 2 × 5 + 2 × (5 + 3)]
Here, number of potatoes = 10
The up-down distance of the bucket:
From the 1st potato = [5 m] × 2 = 10 m
From the 2nd potato = [(5 + 3) m] × 2 = 16 m
From the 3rd potato = [(5 + 3 + 3) m] × 2 = 22 m
From the 4th potato = [(5 + 3 + 3 + 3) m] × 2 = 28 m
.................................. ...........................
∵ 10, 16, 22, 28, ..... are in A.P. such that
a = 10 and d = 16 - 10 = 6
∴ Using Sn = n/2 [2a + (n - 1) d], we have:
S10 = 10/2[2 (10) + (10 - 1) × 6]
= 5 [20 + 9 × 6]
= 5 [20 + 54]
= 5 [74]
= 5 × 74 = 370
Thus, the sum of above distances = 370 m.
⇒ The competitor has to run a total distance of 370 m.
Exercise 5.4
Q1: Which term of the AP: 121, 117, 113, . . ., is its first negative term? [Hint: Find n for an < 0]
Given the AP series is 121, 117, 113, . . .,
Thus, first term, a = 121
Common difference, d = 117-121= -4
By the nth term formula,
an = a+(n −1)d
Therefore,
an = 121+(n−1)(-4)
= 121-4n+4
=125-4n
To find the first negative term of the series, an < 0
Therefore,
125-4n < 0
125 < 4n
n>125/4
n>31.25
Therefore, the first negative term of the series is 32nd term.
Q2: The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
From the given statements, we can write,
a3 + a7 = 6 …………………………….(i)
And
a3 ×a7 = 8 ……………………………..(ii)
By the nth term formula,
an = a+(n−1)d
Third term, a3 = a+(3 -1)d
a3 = a + 2d………………………………(iii)
And Seventh term, a7= a+(7-1)d
a7 = a + 6d ………………………………..(iv)
From equation (iii) and (iv), putting in equation(i), we get,
a+2d +a+6d = 6
2a+8d = 6
a+4d=3
or
a = 3–4d …………………………………(v)
Again putting the eq.(iii) and (iv), in eq. (ii), we get,
(a+2d)×(a+6d) = 8
Putting the value of a from equation (v), we get,
(3–4d +2d)×(3–4d+6d) = 8
(3 –2d)×(3+2d) = 8
32 – 2d2 = 8
9 – 4d2 = 8
4d2 = 1
d = 1/2 or -1/2
Now, by putting both the values of d, we get,
a = 3 – 4d = 3 – 4(1/2) = 3 – 2 = 1, when d = 1/2
a = 3 – 4d = 3 – 4(-1/2) = 3+2 = 5, when d = -1/2
We know, the sum of nth term of AP is;
Sn = n/2 [2a +(n – 1)d]
So, when a = 1 and d=1/2
Then, the sum of first 16 terms are;
S16 = 16/2 [2 +(16-1)1/2] = 8(2+15/2) = 76
And when a = 5 and d= -1/2
Then, the sum of first 16 terms are;
S16 = 16/2 [2.5+(16-1)(-1/2)] = 8(5/2)=20
Q3: A ladder has rungs 25 cm apart. (see Fig. 5.7). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are 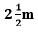 apart, what is the length of the wood required for the rungs? [Hint: Number of rungs = -250/25 ].
apart, what is the length of the wood required for the rungs? [Hint: Number of rungs = -250/25 ].
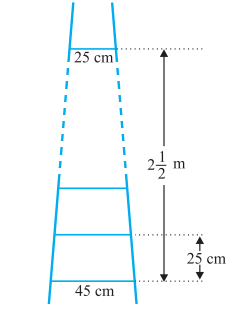
Given,
Distance between the rungs of the ladder is 25cm.
Distance between the top rung and bottom rung of the ladder is =
= 5/2 ×100cm
= 250cm
Therefore, total number of rungs = 250/25 + 1 = 11
As we can see from the figure, the ladder has rungs in decreasing order from top to bottom. Thus, we can conclude now, that the rungs are decreasing in an order of AP.
And the length of the wood required for the rungs will be equal to the sum of the terms of AP series formed.
So,
First term, a = 45
Last term, l = 25
Number of terms, n = 11
Now, as we know, sum of nth terms is equal to,
Sn= n/2(a+ l)
Sn= 11/2(45+25) = 11/2(70) = 385 cm
Hence, the length of the wood required for the rungs is 385cm.
Q.4. The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x. [Hint :Sx – 1 = S49 – Sx ]
Given,
Row houses are numbers from 1,2,3,4,5…….49.
Thus we can see the houses numbered in a row are in the form of AP.
So,
First term, a = 1
Common difference, d=1
Let us say the number of xth houses can be represented as;
Sum of nth term of AP = n/2[2a+(n-1)d]
Sum of number of houses beyond x house = Sx-1
= (x-1)/2[2.1+(x-1-1)1]
= (x-1)/2 [2+x-2]
= x(x-1)/2 ………………………………………(i)
By the given condition, we can write,
S49 – Sx = {49/2[2.1+(49-1)1]}–{x/2[2.1+(x-1)1]}
= 25(49) – x(x + 1)/2 ………………………………….(ii)
As per the given condition, eq.(i) and eq(ii) are equal to each other;
Therefore,
x(x-1)/2 = 25(49) – x(x-1)/2
x = ±35
As we know, the number of houses cannot be a negative number. Hence, the value of x is 35.
Q5: A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of 1 4 m and a tread of 1 2 m. (see Fig. 5.8). Calculate the total volume of concrete required to build the terrace. [Hint : Volume of concrete required to build the first step = ¼ ×1/2 ×50 m3.]
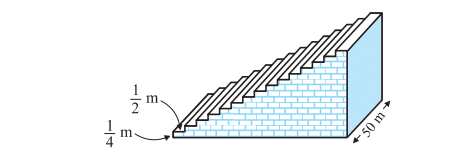
As we can see from the given figure, the first step is ½ m wide, 2nd step is 1m wide and 3rd step is 3/2m wide. Thus we can understand that the width of step by ½ m each time when height is ¼ m. And also, given length of the steps is 50m all the time. So, the width of steps forms a series AP in such a way that;
½ , 1, 3/2, 2, ……..
Volume of steps = Volume of Cuboid
= Length × Breadth HeightNow,
Volume of concrete required to build the first step = ¼ ×1/2 ×50 = 25/4
Volume of concrete required to build the second step =¼ ×1/×50 = 25/2
Volume of concrete required to build the second step = ¼ ×3/2 ×50 = 75/2Now, we can see the volumes of concrete required to build the steps, are in AP series;
25/4 , 25/2 , 75/2 …..Thus, applying the AP series concept,
First term, a = 25/4Common difference, d = 25/2 – 25/4 = 25/4
As we know, the sum of n terms is;
Sn = n/2[2a+(n-1)d] = 15/2(2×(25/4 )+(15/2 -1)25/4)
Upon solving, we get,
Sn = 15/2 (100)
Sn = 750
Hence, the total volume of concrete required to build the terrace is 750 m3.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 5 - Arithmetic Progressions (Exercise 5.2)
| 1. What are arithmetic progressions? |  |
| 2. How can we find the nth term of an arithmetic progression? |  |
| 3. How do we determine if a given sequence is an arithmetic progression? |  |
| 4. What is the sum of the first n terms of an arithmetic progression? |  |
| 5. How can we find the common difference of an arithmetic progression if the first and last terms are given? |  |