NCERT Solutions for Class 10 Maths Chapter 7 - Coordinate Geometry (Exercise 7.1)
Q1. Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
Ans: Let P(2, 3) and Q(4, 1)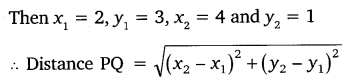
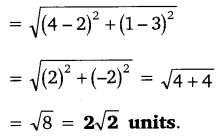
(ii) (-5, 7), (-1, 3)
Ans: Let P (-5, 7) and Q (-1, 3)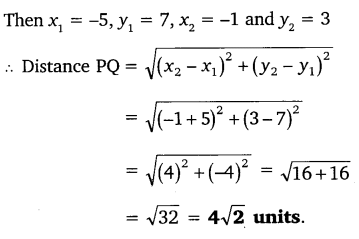
(iii) (a, b), (-a, -b)
Ans: Let P (a, b) and Q (-a, -b)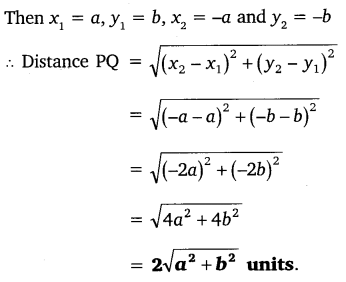
Q2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2?
Ans: Let points be A (0, 0) and B (36, 15)
The distance between the two points is: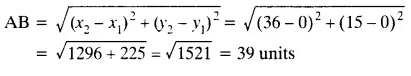
The distance between towns A and B will be 39 km.
Q3. Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Ans: Let points be A(1, 5), B(2, 3) and C(-2, -11)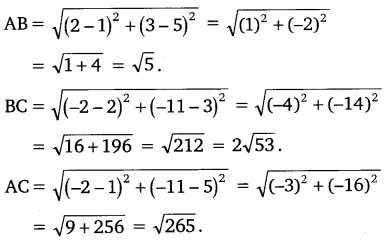
AB + BC ≠ AC
Hence, the given points are not collinear.
Q4. Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Ans: Since two sides of any isosceles triangle are equal. To check whether the given points are vertices of an isosceles triangle, we will find the distance between all the points.
Let the points be A (5, -2), B (6, 4) and C (7, -2).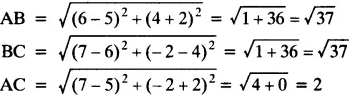
Here AB = BC
∴ Δ ABC is an isosceles.
Q5. In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, ‘‘Don’t you think ABCD is a square?’’ Chameli disagrees. Using distance single formula, find which of them is correct.
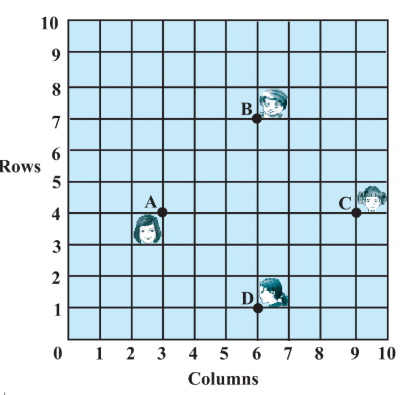 Ans: Points A (3, 4), B (6, 7), C (9, 4) and D (6, 1)
Ans: Points A (3, 4), B (6, 7), C (9, 4) and D (6, 1)
∴ ABCD is a square.
Hence, Champa is correct.
Q6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
Ans: Let the points be: A (-1, -2), B (1, 0), C (-1, 2) and D (-3, 0).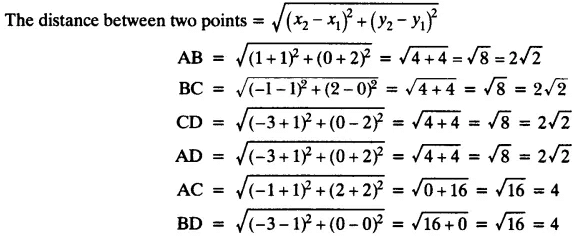
Here AC = BD, AB = BC = CD = AD
Hence, the quadrilateral ABCD is a square.
(ii) (-3, 5), (3, 1), (0, 3), (-1, - 4)
Let points be A (-3, 5), B (3, 1), C (0, 3) and D (-1, -4)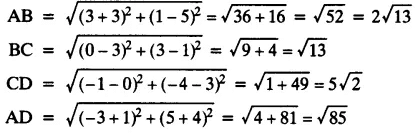
It is seen that points A, B and C are collinear.
So, the given points can only form 3 sides i.e, a triangle and not a quadrilateral that has 4 sides.
Therefore, the given points do not form any quadrilateral.
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Let points be A (4, 5), B (7, 6), C (4, 3) and D (1, 2)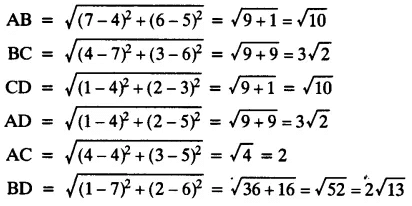
Here, AB = CD, BC = AD and AC ≠ BD
∴ The quadrilateral ABCD is a parallelogram.
Q7. Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
Ans: Let points be A (2, -5) and B (-2, 9)
Let P (x, 0) be the point on the x-axis.
PA = PB
Then, PA2 = PB2
⇒ (x - 2)2 + (0 + 5)2 = (x + 2)2 + (0 - 9)2
⇒ (x - 2)2 - (x + 2)2 = 81 - 25
⇒ (x - 2 + x + 2)(x - 2 - x - 2) = 56
⇒ (2x)(-4) = 56
⇒ -8x = 56
⇒ x = -7
Hence, the required point is (-7, 0).
Q8. Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
Ans: Points P (2, -3), Q (10, y) and PQ = 10 units
The distance between the two points is: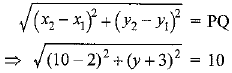
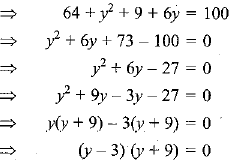
⇒ y - 3 = 0 or y + 9 = 0
⇒ y = 3 or - 9
Q9. If Q (0, 1) is equidistant from P (5, -3) and R (x, 6), find the values of x. Also, find the distances QR and PR.
Ans: PQ = QR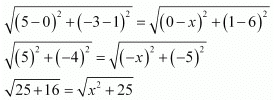
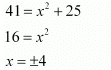
Therefore, point R is (4, 6) or (−4, 6).
When point R is (4, 6),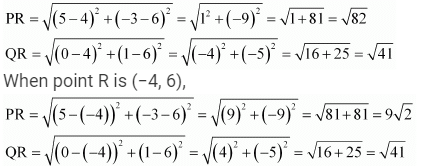
Q10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (-3, 4).
Ans: Points A (3, 6), B (-3, 4) are given and point P(x, y) is equidistant from points A and B.
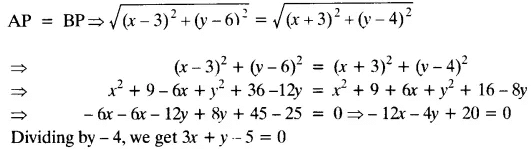
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 7 - Coordinate Geometry (Exercise 7.1)
| 1. What is the distance formula in coordinate geometry? |  |
| 2. How do you find the midpoint of a line segment in coordinate geometry? |  |
| 3. What are the coordinates of points that lie on the x-axis and y-axis? |  |
| 4. How do you determine if three points are collinear in coordinate geometry? |  |
| 5. What is the slope of a line in coordinate geometry, and how is it calculated? |  |

















