Facts that Matter: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
Trigonometric Ratios
The certain ratios involving the sides of a right-angled triangle are called trigonometric ratios. Look at the adjoining right triangle ABC, right-angled at B. The Trigonometric Ratios of angle A are:
Reciprocals of the above T-ratios are: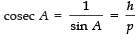
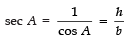
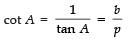
NOTE:
I. ‘sin θ ’ is a single symbol and ‘sin’ cannot be detached from ‘θ ’. sin θ ≠ sin × θ. This remark is true for other t-ratios also.
II. The values of the trigonometric ratios of an angle depend only on the magnitude of the angle and not on the lengths of the sides of the triangle.
III. In a right angle, the hypotenuse is the longest side, therefore, the value of sin A or cos A is always less than 1 or at the most equal to 1.
Trigonometric Ratios of Some Specific Angles
The specific angles are 0°, 30°, 45°, 60° and 90°. Trigonometric ratios of these angles are given in the following table:
NOTE:
I. The value of sin A increases from 0 to 1, as A increases from 0° to 90°.
II. The value of cos A decreases from 1 to 0, as A increases from 0° to 90°.
III. The value of tan A increases from 0 to ∞ , as A increases from 0° to 90°.
IV. √2 = 1.414 and √3 = 1.732.
Trigonometric Identities
Since an equation is called an identity when it is true for all the values of the variables involved.
So, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angles involved. Some of the useful trigonometric identities:
(i) cos2A + sin2A = 1
(ii) 1 + tan2A = sec2A
(iii) cot2A + 1 = cosec2A
|
127 videos|584 docs|79 tests
|
FAQs on Facts that Matter: Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What are trigonometric ratios? |  |
| 2. How can trigonometric ratios be used to find missing side lengths in a right triangle? |  |
| 3. What are the trigonometric ratios for the angles 0°, 30°, 45°, 60°, and 90°? |  |
| 4. Can trigonometric ratios be negative? |  |
| 5. How are trigonometric ratios used in real-life applications? |  |

















