Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Facts that Matter: Surface Areas & Volumes
Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10 PDF Download
1. Cube
For a Cube of side a we have: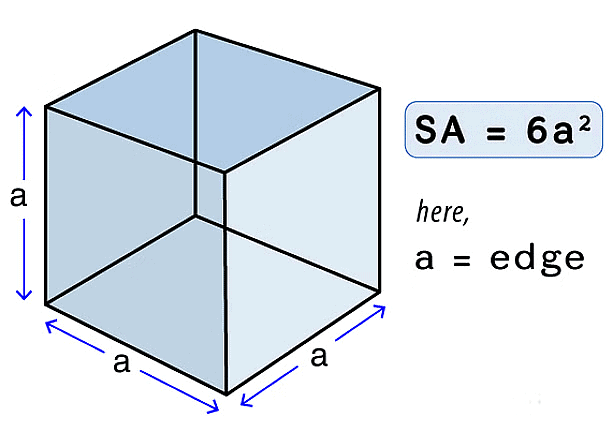
(i) Volume = (a3) cu. units.
(ii) Lateral surface area = [4a2] sq. units.
(iii) Total surface area = [6a2] sq. units.
2. Cuboid
For a Cuboid of length = l, breadth = b and height = h, we have:
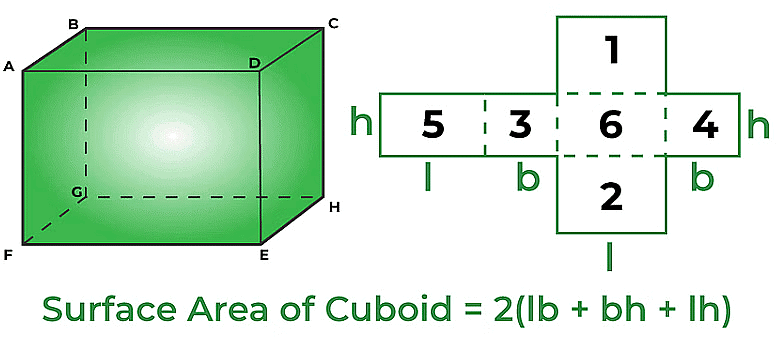(i) Volume = (l × b × h) cu. units.
(ii) Lateral surface area = [2 (l + b) × h] sq. units.
(iii) Total surface area = [2 (lb + bh + hl] sq. units.
3. Cylinder
For a Cylinder of base radius = r and height (or length) = h, we have:
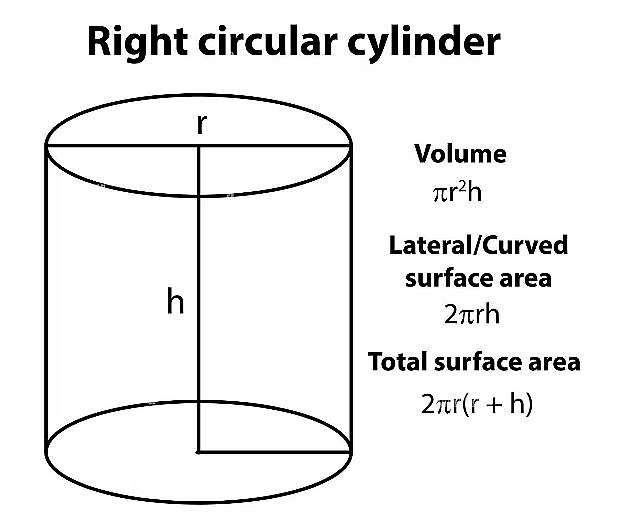(i) Volume = πr2h cu. units.
(ii) Curved surface area = 2πrh sq. units.
(iii) Total surface area = 2πr (h + r) sq. units.
4. Hollow Cylinder
For a Hollow Cylinder having external radius = R, internal radius = r and height = h, we have:
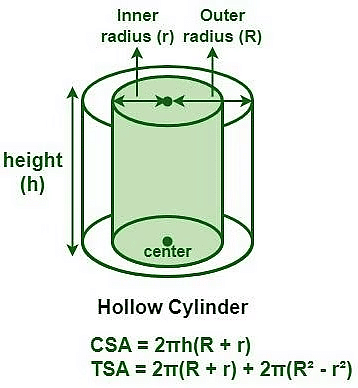(i) Volume= [External volume] − [Internal volume]
=(πR2h − πr2h) cu. units = π(R2 − r2) cu. units.
(ii) Curved surface area= [External S.A.] + [Internal S.A.]
=[2πRh + 2πrh] sq. units = 2πh (R + r) sq. units
(iii) Total surface area= (curved S.A.) + (area of the base-ring)
= [(2πRh + 2πrh) + 2 (πR2 − πr2)] sq. units
= [(2πh (R + r) + 2π (R2 − r2)] sq. units
5. Cone
For a Cone of base radius = r, height = h and slant height l =√h2+r2we have:
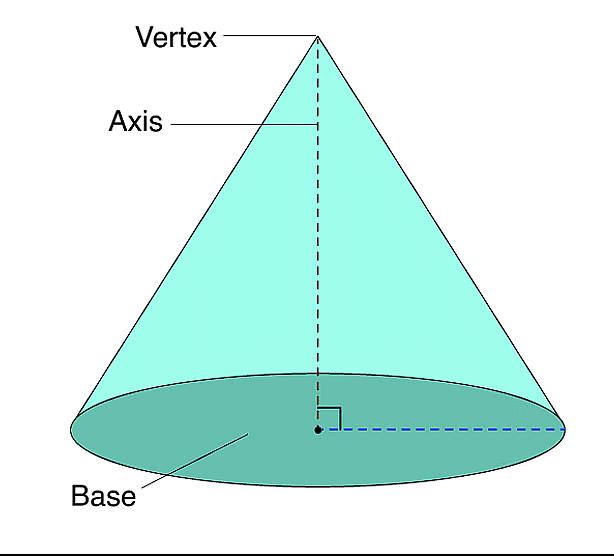(i) Volume = 1/3 πr2h cu. units.
(ii) Curved surface area = πrl sq. units.
(iii) Total surface area = [Curved surface area] + [Area of base]
= [πrl + πr2] sq. units = πr (l + r) sq. units.
6. Sphere
For a Sphere of radius r, we have:
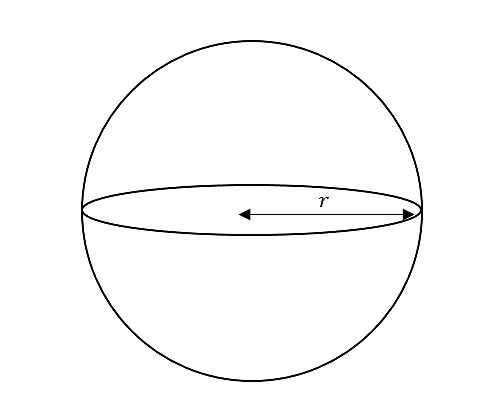(i) Volume = 4/3 πr3 cu. units.
(ii) Curved surface area = 4πr2 sq. units.
(iii) Total surface area =4πr2sq. units.
7. Hemisphere
For a Hemisphere of radius r, we have:
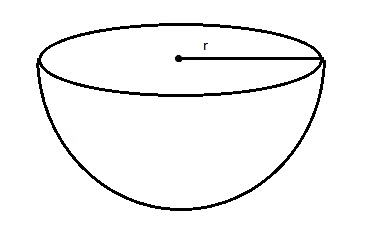(i) Volume = 2/3 πr3 cu. units.
(ii) Surface area = 2πr2 sq. units.
(iii) Total surface area = 3πr2 sq. units.
The document Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|584 docs|79 tests
|
FAQs on Facts that Matter: Surface Areas & Volumes - Mathematics (Maths) Class 10
| 1. What is the formula for calculating the surface area of a sphere? |  |
Ans. The formula for calculating the surface area of a sphere is \( 4\pi r^2 \), where \( r \) is the radius of the sphere.
| 2. How do you find the volume of a cylinder? | |
Ans. The volume of a cylinder can be calculated using the formula \( V = \pi r^2 h \), where \( r \) is the radius of the base and \( h \) is the height of the cylinder.
| 3. What is the difference between surface area and volume? | |
Ans. Surface area refers to the total area that the surface of a three-dimensional object occupies, while volume measures the amount of space inside that object.
| 4. How is the volume of a cone calculated? | |
Ans. The volume of a cone is calculated using the formula \( V = \frac{1}{3}\pi r^2 h \), where \( r \) is the radius of the base and \( h \) is the height of the cone.
| 5. Can you explain how to find the surface area of a rectangular prism? | |
Ans. To find the surface area of a rectangular prism, use the formula \( SA = 2(lw + lh + wh) \), where \( l \) is the length, \( w \) is the width, and \( h \) is the height of the prism.
About this Document
2.6K Views
4.95/5
Rating
Sep 27, 2025
Last updated
Document Description: Facts that Matter: Surface Areas & Volumes for Class 10 2025 is part of Mathematics (Maths) Class 10 preparation.
The notes and questions for Facts that Matter: Surface Areas & Volumes have been prepared according to the Class 10 exam syllabus. Information about Facts that Matter: Surface Areas & Volumes covers topics
like and Facts that Matter: Surface Areas & Volumes Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Facts that Matter: Surface Areas & Volumes.
Introduction of Facts that Matter: Surface Areas & Volumes in English is available as part of our Mathematics (Maths) Class 10
for Class 10 & Facts that Matter: Surface Areas & Volumes in Hindi for Mathematics (Maths) Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10
Description
Full syllabus notes, lecture & questions for Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Facts that Matter: Surface Areas & Volumes
In this doc you can find the meaning of Facts that Matter: Surface Areas & Volumes defined & explained in the simplest way possible. Besides explaining types of
Facts that Matter: Surface Areas & Volumes theory, EduRev gives you an ample number of questions to practice Facts that Matter: Surface Areas & Volumes tests, examples and also practice Class 10
tests
Related Searches
Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10
,past year papers
,Summary
,Free
,Extra Questions
,Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10
,ppt
,video lectures
,MCQs
,study material
,practice quizzes
,Facts that Matter: Surface Areas & Volumes | Mathematics (Maths) Class 10
,mock tests for examination
,Objective type Questions
,Semester Notes
,shortcuts and tricks
,Previous Year Questions with Solutions
,Important questions
,Sample Paper
,Viva Questions
,Exam
;
Additional Information about Facts that Matter: Surface Areas & Volumes for Class 10 Preparation
Facts that Matter: Surface Areas & Volumes Free PDF Download
The Facts that Matter: Surface Areas & Volumes is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Facts that Matter: Surface Areas & Volumes now and kickstart your journey towards success in the Class 10 exam.
Importance of Facts that Matter: Surface Areas & Volumes
The importance of Facts that Matter: Surface Areas & Volumes cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Facts that Matter: Surface Areas & Volumes Notes
Facts that Matter: Surface Areas & Volumes Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Facts that Matter: Surface Areas & Volumes.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Facts that Matter: Surface Areas & Volumes Notes on EduRev are your ultimate resource for success.
Facts that Matter: Surface Areas & Volumes Class 10 Questions
The "Facts that Matter: Surface Areas & Volumes Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Facts that Matter: Surface Areas & Volumes on the App
Students of Class 10 can study Facts that Matter: Surface Areas & Volumes alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Facts that Matter: Surface Areas & Volumes,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Facts that Matter: Surface Areas & Volumes is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup