B Com Exam > B Com Notes > Business Mathematics and Statistics > Finding areas using integration, Business Mathematics & Statistics
Finding areas using integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
Area Under a Curve
Calculating the area under a curve.
Definite Integrals
So far when integrating, there has always been a constant term left. For this reason, such integrals are known as indefinite integrals. With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need for any unknown constant terms [the constant cancels out].
The Area Under a Curve
The area under a curve between two points can be found by doing a definite integral between the two points.
To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.
Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area which is partly above and partly below the x-axis.
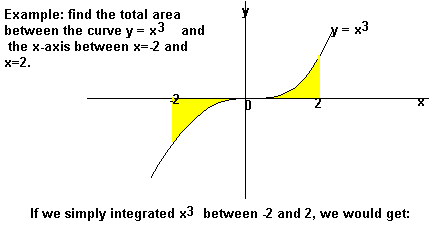
You may also be asked to find the area between the curve and the y-axis. To do this, integrate with respect to y.
Example
Find the area bounded by the lines y = 0, y = 1 and y = x2.
The document Finding areas using integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com is a part of the B Com Course Business Mathematics and Statistics.
All you need of B Com at this link: B Com
|
115 videos|142 docs
|
FAQs on Finding areas using integration, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is integration and how is it used to find areas? |  |
Ans. Integration is a mathematical technique that allows us to find the area under a curve or between two curves. By integrating a function, we can calculate the total area enclosed by the curve(s) and the x-axis. This is achieved by breaking the region into infinitesimally small rectangles and summing up their areas using the definite integral.
| 2. Can integration be used to find areas in business and economics? | |
Ans. Yes, integration is extensively used in business and economics to calculate areas and solve various problems. For example, it can be used to determine the area under a demand curve to find the total revenue or to calculate the area between a supply curve and the equilibrium price to find the producer surplus.
| 3. Are there any limitations to using integration for finding areas in real-world scenarios? | |
Ans. While integration is a powerful tool for finding areas, there are some limitations in real-world scenarios. One limitation is that integration assumes a continuous and well-behaved function, which may not always accurately represent real-world data. Additionally, practical constraints such as limited data points or non-linear relationships can make integration challenging to apply directly.
| 4. Can integration be used to find areas of irregular shapes or regions? | |
Ans. Yes, integration can be used to find areas of irregular shapes or regions. By breaking down the irregular shape into smaller, manageable pieces, we can integrate the functions that describe each piece to find their individual areas. Summing up these areas using the definite integral allows us to calculate the total area of the irregular shape.
| 5. How does integration relate to business decision-making and optimization? | |
Ans. Integration plays a crucial role in business decision-making and optimization. By using integration techniques, businesses can analyze and optimize various aspects such as production costs, profit margins, and resource allocation. Integration helps in determining optimal production levels, pricing strategies, and maximizing profits by finding areas that represent relevant economic measures in these decision-making processes.
Related Exams
About this Document
|
4.95/5 Rating |
|
Dec 23, 2024 Last updated |
Document Description: Finding areas using integration, Business Mathematics & Statistics for B Com 2024 is part of Business Mathematics and Statistics preparation.
The notes and questions for Finding areas using integration, Business Mathematics & Statistics have been prepared according to the B Com exam syllabus. Information about Finding areas using integration, Business Mathematics & Statistics covers topics
like Area Under a Curve and Finding areas using integration, Business Mathematics & Statistics Example, for B Com 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Finding areas using integration, Business Mathematics & Statistics.
Introduction of Finding areas using integration, Business Mathematics & Statistics in English is available as part of our Business Mathematics and Statistics
for B Com & Finding areas using integration, Business Mathematics & Statistics in Hindi for Business Mathematics and Statistics course.
Download more important topics related with notes, lectures and mock test series for B Com
Exam by signing up for free. B Com: Finding areas using integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com
Description
Full syllabus notes, lecture & questions for Finding areas using integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com - B Com | Plus excerises question with solution to help you revise complete syllabus for Business Mathematics and Statistics | Best notes, free PDF download
Information about Finding areas using integration, Business Mathematics & Statistics
In this doc you can find the meaning of Finding areas using integration, Business Mathematics & Statistics defined & explained in the simplest way possible. Besides explaining types of
Finding areas using integration, Business Mathematics & Statistics theory, EduRev gives you an ample number of questions to practice Finding areas using integration, Business Mathematics & Statistics tests, examples and also practice B Com
tests
|
Explore Courses for B Com exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Objective type Questions
,Summary
,Previous Year Questions with Solutions
,Important questions
,Free
,Semester Notes
,Business Mathematics & Statistics | Business Mathematics and Statistics - B Com
,Finding areas using integration
,shortcuts and tricks
,MCQs
,ppt
,video lectures
,Finding areas using integration
,Business Mathematics & Statistics | Business Mathematics and Statistics - B Com
,Viva Questions
,practice quizzes
,Finding areas using integration
,Business Mathematics & Statistics | Business Mathematics and Statistics - B Com
,Exam
,mock tests for examination
,past year papers
,Sample Paper
,Extra Questions
,study material
;
Additional Information about Finding areas using integration, Business Mathematics & Statistics for B Com Preparation
Finding areas using integration, Business Mathematics & Statistics Free PDF Download
The Finding areas using integration, Business Mathematics & Statistics is an invaluable resource that delves deep into the core of the B Com exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Finding areas using integration, Business Mathematics & Statistics now and kickstart your journey towards success in the B Com exam.
Importance of Finding areas using integration, Business Mathematics & Statistics
The importance of Finding areas using integration, Business Mathematics & Statistics cannot be overstated, especially for B Com aspirants.
This document holds the key to success in the B Com exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Finding areas using integration, Business Mathematics & Statistics Notes
Finding areas using integration, Business Mathematics & Statistics Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Finding areas using integration, Business Mathematics & Statistics.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Finding areas using integration, Business Mathematics & Statistics Notes on EduRev are your ultimate resource for success.
Finding areas using integration, Business Mathematics & Statistics B Com Questions
The "Finding areas using integration, Business Mathematics & Statistics B Com Questions" guide is a valuable resource for all aspiring students preparing for the
B Com exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Finding areas using integration, Business Mathematics & Statistics on the App
Students of B Com can study Finding areas using integration, Business Mathematics & Statistics alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Finding areas using integration, Business Mathematics & Statistics,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Finding areas using integration, Business Mathematics & Statistics is prepared as per the latest B Com syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup