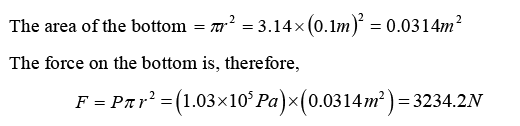Fluid Statics | Mechanics & General Properties of Matter - Physics PDF Download
Fluids
Matter is broadly divided into three categories, solid, liquid and gas. The intermolecular forces are strong in solids, so that the shape and size of solids do not easily change. This force is comparatively less in liquids and so the shape is easily changed. Although the shape of a liquid can be easily changed, the volume of a given mass of a liquid is not so easy to change. It needs quite a good effort to change the density of liquids. In gases, the intermolecular forces are very small and it is simple to change both the shape and the density of a gas. We shall assume that the liquids we deal with are incompressible and non viscous. The first condition means that the density of the liquid is independent of the variations in pressure and always remains constant. The second condition means that parts of the liquid in contact do not exert any tangential force on each other. The force by one part of the liquid on the other part is perpendicular to the surface of contact. Thus, there is no friction between the adjacent layers of a liquid.
Pressure in a Fluid
Consider a point A in the fluid (figure 1).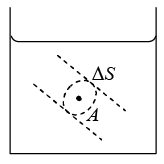
Imagine a small area ΔS containing the point A . The fluid on one side of the area presses the fluid on the other side and vice versa. Let the common magnitude of the forces be F . Then the pressure of the fluid at the point A as
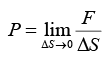 ....(1)
....(1)
For a homogeneous and nonviscous fluid, this quantity does not depend on the orientation of ΔS and hence we talk of pressure at a point. For such a fluid, pressure is a scalar quantity having only magnitude.
Unit of Pressure
The S.I. unit of pressure is N/m2 called Pascal (Pa).
Variation of Pressure with Height
Let us consider two points A and B (figure 2) separated by a small vertical height dz . Imagine a horizontal area ΔS1 containing A and an identical horizontal area ΔS2 containing B . The area ΔS1 = ΔS2 = ΔS . Consider the fluid enclosed between the two surfaces ΔS1, ΔS2 and the vertical boundary joining them. The vertical forces acting on this fluid are
(a) F1, vertically upward by the fluid below it
(b) F2 vertically downward by the fluid above it and
(c) weight W ,vertically downward Let the pressure at the surface A be P and the pressure at B be P + dP . Then
F1 = PΔS and F2 = (P+ dP) ΔS.
The volume of the fluid considered is (ΔS)(dz). If the density of the fluid at A is ρ, the mass of the fluid considered is ρ(ΔS)(dz) and hence its weight W is W = ρ(ΔS)(dz)g .
For vertical equilibrium,
F1 = F2 + W
Or PΔS = P + dP ΔS + ρg (dz)ΔS
or dP = - ρg (dz) …(2)
As we move up through a height dz the pressure decreases by ρg dz where ρ is the density of the fluid at that point.
Now consider two points at z = 0 and z = h . If the pressure at z = 0 is P1 and that of at z = h is P2, then from equation (2),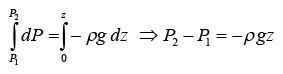
P1 = P2 + ρgz .…(3)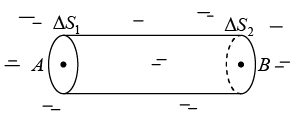 Next consider two points A and B in the same horizontal line inside a fluid. Imagine a small vertical area ΔS1 containing the point A and a similar vertical area ΔS2 containing the point B .
Next consider two points A and B in the same horizontal line inside a fluid. Imagine a small vertical area ΔS1 containing the point A and a similar vertical area ΔS2 containing the point B .
The area ΔS1 = ΔS2 = ΔS Consider the contained in the horizontal cylinder bounded and ΔS and ΔS2. If the pressures at A and B are P1 and P2 respectively, the forces in the direction AB are
(a) P1ΔS towards right and
(b) P2ΔS towards left.
If the fluid remains in equilibrium, P1ΔS = P2ΔS or P1 = P2
Thus, the pressure is same at two in the same horizontal level.
Pascal’s Law
We have seen in the previous section that the pressure difference between two points in a liquid at rest depends only on the difference in vertical height between the points. The difference is in fact ρgz , where ρ is the density of the liquid (assumed constant) and z is the difference in vertical height.
If the pressure in a liquid is changed at a particular point, the change is transmitted to the entire liquid without being diminished in magnitude.
As an example, suppose a flask fitted with a piston is filled with a liquid as shown in figure (4). Let an external force F be applied on the piston. If the cross-sectional area of the piston is A , the pressure just below the piston is increased by F/A . By Pascal’s law, the pressure at any point B will also increase by the same amount F/A . This is because the pressure at B has to be ρgz more than the pressure at the piston, where z is the vertical distance of B below the piston.
By applying the force we do not appreciably change z (as the liquid is supposed to be incompressible) and hence the pressure difference remains unchanged. As the pressure at the piston is increased by F/A , the pressure at B also increases by the same amount.
Atmospheric Pressure and Barometer
The atmosphere of the earth is spread upto a height of about 200 km . This atmosphere presses the bodies on the surface of the earth. The force exerted by the air on any body is perpendicular to the surface of the body. Consider a small surface ΔS in contact with air. If the force exerted by the air on this part is F, the atmospheric pressure is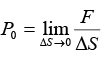
Atmospheric pressure at the top of the atmosphere is zero as there is nothing above it to exert the force. The pressure at a distance z below the top will be 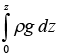 Remember, neither ρ nor g can be treated as constant over large variations in heights. However, the density of air is quite small and so the atmospheric pressure does not vary appreciably over small distances. Thus, we say that the atmospheric pressure at Patna is 76 cm of mercury without specifying whether it is at Gandhi Maidan or at the top of Golghar.
Remember, neither ρ nor g can be treated as constant over large variations in heights. However, the density of air is quite small and so the atmospheric pressure does not vary appreciably over small distances. Thus, we say that the atmospheric pressure at Patna is 76 cm of mercury without specifying whether it is at Gandhi Maidan or at the top of Golghar.
Torricelli devised an ingenious way to measure the atmospheric pressure. The instrument is known as barometer. In this, a glass tube open at one end and having a length of about a meter is filled with mercury. The open end is temporarily closed (by a thumb or otherwise) and the tube is inverted in a cup of mercury. With the open end dipped into the cup, the temporary closure is removed. The mercury column in the tube falls down a little and finally stays there.
Figure (5) shows schematically the situation. The upper part of the tube contains vacuum as the mercury goes down and no air is allowed in.
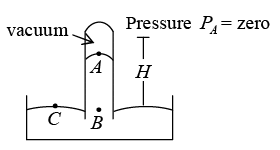
Thus, the pressure at the upper end A of the mercury column inside the tube is PA = 0 . Let us consider a point C on the mercury surface in the cup and another point B in the tube at the same horizontal level. The pressure at C is equal to the atmospheric pressure. As B and C are in the same horizontal level, the pressures at B and C are equal. Thus, the pressure at B is equal to the atmospheric pressure P0 in the lab.
Suppose the point B is at a depth H below A . If ρ be the density of mercury,
PB = PA + ρgH or, P0 = ρgH ...(4)
The height H of the mercury column in the tube above the surface in the cup is measured. Knowing the density of mercury and the acceleration due to gravity, the atmospheric pressure can be calculated using equation (4).
The atmospheric pressure is often given as the length of mercury column in a barometer. Thus, a pressure of 76 cm of mercury means
P0 = (13.6 × 103 kg/m3)(9.8m/s2)(0.76m) = 1.01×105 Pα.
This pressure is written as 1 atm. If the tube is insufficient in length, the mercury column will not fall down and no vacuum will be created. The inner surface of the tube will be in contact with the mercury at the top and will exert a pressure PA on it.
Example 1: Water is filled in a flask upto a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pα, find the force exerted by the water on the bottom. Take g = 10m / s and density of water = 1000 kg/m
The pressure at the surface of the water is equal to the atmospheric pressure P0. The pressure at the bottom is
P = P0 + hρg = 1.01 X 105 Pα + (0.20m) (1000 kg/m3)(10m/s2)
= 1.01 x 105 Pα + 0.02 x 105 Pα = 1.03 x 105 Pα
The area of the bottom = πr2 = 3.14 × (0.1m)2 = 0.0314m2
The force on the bottom is, therefore,
F = Pπr2 = (1.03 × 105 Pα ) × (0.0314 m2) = 3234.2 N
Manometer
Manometer is a simple device to measure the pressure in a closed vessel containing a gas. It consists of a U - tube having some liquid. One end of the tube is open to the atmosphere and the other end is connected to the vessel (figure 6).

The pressure of the gas = the pressure at A = pressure at B = pressure at C + hρg = P0 + hρg. Where, P0 is the atmospheric pressure, h = BC is the difference in levels of the liquid in the two arms and ρ is the density of the liquid.
The excess pressure P - P0 is called the gauge pressure.
 |
Download the notes
Fluid Statics
|
Download as PDF |
Archimedes’ Principle
When a body is partially or fully dipped into a fluid, the fluid exerts forces on the body. At any small portion of the surface of the body, the force by the fluid is perpendicular to the surface and is to the pressure at that point multiplied by the area (figure 8). The resultant of all these contact forces is called the force of buoyancy or buoyant force.
Archimedes’ principle states that when a body is partially or fully dipped into a fluid at rest, the fluid exerts an upward force of buoyancy equal to the weight of the displaced fluid.
Archimedes’ principle is not an independent principle and may be deduced from Newton’s laws of motion.
Consider the situation shown in figure 7, where a body is shown dipped into a fluid. Suppose the body dipped in the fluid is replaced by the same ‘fluid of equal volume. As the entire fluid now becomes homogeneous, all parts will remain in equilibrium. The part of the fluid substituting the body also remains in equilibrium.
Forces acting on this substituting fluid are
(a) the weight mg of this part of the fluid and
(b) the resultant B of the’ contact forces by the remaining fluid.
As the substituting fluid is in equilibrium, these two should be equal and opposite. Thus,
B = mg … (5)
and it acts in the vertically upward direction.
Floatation
When a solid body is dipped into a fluid, the fluid exerts an upward force of buoyancy on the solid. If the force of buoyancy equals the weight of the solid, the solid will remain in equilibrium. This is called floatation. When the overall density of the solid is smaller than the density of the fluid, the solid floats with a part of it in the fluid. The fraction dipped is such, that the weight of the displaced fluid equals the weight of the solid.
Example 2: A 700 g solid cube having an edge of length 10 cm floats in water. How much volume of the cube is outside the water? Density of water = 1000 kg/m3.
The weight of the cube is balanced by the buoyant force. The buoyant force is equal to the weight of the water displaced. If a volume V of the cube is inside the water, the weight of the displaced water = V ρg , where ρ is the density of water.
Thus, V ρg = (0.7 kg)g ⇒ V == 7 x 10-4 m3 = 700 cm3
The total volume o the cube = (10 cm)3 = 1000 cm3
The volume outside the water is 1000 cm3 - 700 cm3 = 300 cm3.
Pressure Difference and Buoyant Force in Accelerating Fluids
Equations (3) and (5) were derived by assuming that the fluid under consideration is in equilibrium in an inertial frame. If this is not the case, the equations must be modified. We shall discuss some special cases of accelerating fluids.
A Liquid Placed in an Elevator
(a) Pressure Difference: Suppose a beaker contains some liquid and it is placed in an elevator which is going up with acceleration α0 (figure 8).
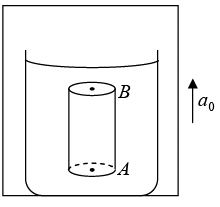
Let A and B be two points in the liquid, B being at a vertical height z above A. Construct a small horizontal area ΔS around A and an equal horizontal area around B . Construct a vertical cylinder with the two areas as the faces. Consider the motion of the liquid contained within this cylinder. Let P1 be the pressure at A and P2 be the pressure at B.
Forces acting on the liquid contained in the cylinder, in the vertical direction, are
(a) P1ΔS upward due to the liquid below it
(b) P2ΔS downward due to the liquid above it and
(c) weight mg = (ΔS)zρg downward, where ρ is the density of the liquid.
Under the action of these three forces the liquid is accelerating upward with an acceleration a0.
From Newton’s second law
P1ΔS - P2ΔS - mg = mα0
(P1 - P2) ΔS = m(g +α0) = (ΔS)zρ(g + α0)
P1 P2 = ρ(g + α0)z. …(6)
(b) Buoyant Force
Now suppose a body is dipped inside a liquid of density ρ placed in an elevator going up with acceleration a0. Let us calculate the force of buoyancy B on this body. As was done earlier, let us suppose that we substitute the body into the liquid by the same liquid of equal volume. The entire liquid becomes a homogenous mass and hence the substituted liquid is at rest with respect to the rest of the liquid. Thus, the substituted liquid is also going up with an acceleration a together with the rest of the liquid.
The forces acting on the substituted liquid are
(a) the buoyant force B and
(b) the weight mg of the substituted liquid. From Newton’s second law,
From Newton’s second law, 0
B + mg = ma0 or B = m(g + α0) ….(7)
Free Surface of a Liquid in Horizontal Acceleration
Consider a liquid placed in a beaker which is accelerating horizontally with acceleration a0 (figure 9).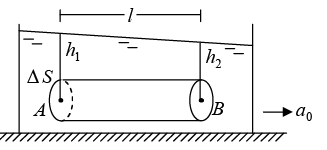
Let A and B be two points in the liquid at a separation l in the same horizontal line along the acceleration a0. We shall first obtain the pressure difference between the points A and B Construct a small vertical area ΔS around A and an equal area around B . Consider the liquid contained in the horizontal cylinder with the two areas as the flat faces.
Let the pressure at A be P1 and the pressure at B be P2. The forces along the line AB are: (a) P1ΔS towards right due to the liquid on the left and
(b) P2ΔS towards left due to the liquid on the right.
Under the action of these forces, the liquid contained in the cylinder is accelerating towards right.
From Newton’s second law,
P1ΔS - P2ΔS = mα0 or (P1 - P2)ΔS = (ΔS)l ρ0
Or P1 - P2 = l ρ0 ....(8)
The two points in the same horizontal line do not have equal pressure if the liquid is accelerated horizontally.
As there is no vertical acceleration, the equation (3) is valid. If the atmospheric pressure is P0, the pressure at A is P1 = P0 + h1ρg and the pressure at B is P2 = P0 + h2ρg, where h1 and h2 are the depths of A and B from the free surface. Substituting in (8),
h1ρg - h2ρg = l ρ α0 or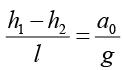 or tan θ = α0/g
or tan θ = α0/g
where θ is the inclination of the free surface with the horizontal.
|
61 videos|23 docs|25 tests
|
FAQs on Fluid Statics - Mechanics & General Properties of Matter - Physics
| 1. What is fluid statics? |  |
| 2. What is pressure in a fluid? |  |
| 3. What is Archimedes' Principle? |  |
| 4. What is the significance of Archimedes' Principle? |  |
| 5. How does pressure change with depth in a fluid? |  |