Frequency Response Analysis of Second Order Control System | Control Systems - Electrical Engineering (EE) PDF Download

What is Frequency Response?

• The response of a system can be partitioned into both the transient response and the steady state response. We can find the transient response by using Fourier integrals. The steady state response of a system for an input sinusoidal signal is known as the frequency response. In this chapter, we will focus only on the steady state response.
• If a sinusoidal signal is applied as an input to a Linear Time-Invariant (LTI) system, then it produces the steady state output, which is also a sinusoidal signal. The input and output sinusoidal signals have the same frequency, but different amplitudes and phase angles.

Let the input signal be −
r(t) = A sin(ω₀t)
The open loop transfer function will be −
G(s) = G(jω)
We can represent G(jω) in terms of magnitude and phase as shown below.
G(jω) = |G(jω)|∠G(jω)
Substitute, ω = ω₀ in the above equation.
G(jω₀) = |G(jω₀)|∠G(jω₀)
The output signal is
c(t) = A|G(jω₀)|sin(ω₀t + ∠G(jω₀))

• The amplitude of the output sinusoidal signal is obtained by multiplying the amplitude of the input sinusoidal signal and the magnitude of G(jω) at ω = ω₀.
• The phase of the output sinusoidal signal is obtained by adding the phase of the input sinusoidal signal and the phase of G(jω) at ω = ω₀.

Where,

• A is the amplitude of the input sinusoidal signal.
• ω₀ is angular frequency of the input sinusoidal signal.

We can write, angular frequency ω₀ as shown below.

• ω₀ = 2πf₀

Here, f₀ is the frequency of the input sinusoidal signal. Similarly, you can follow the same procedure for closed loop control system.

Frequency Domain Specifications

The frequency domain specifications are resonant peak, resonant frequency and bandwidth. Consider the transfer function of the second order closed loop control system as,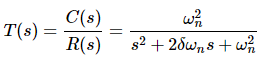

Substitute, s = jω in the above equation.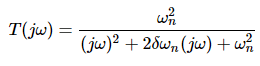



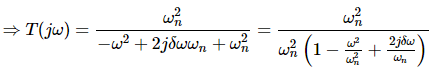
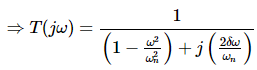
Let, ω/ω_n = u Substitute this value in the above equation.

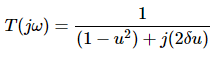
Magnitude of T(jω) is -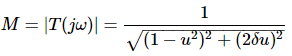

Phase of T(jω) is -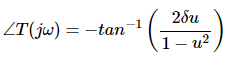

Resonant Frequency
It is the frequency at which the magnitude of the frequency response has peak value for the first time. It is denoted by ω_r. At ω = ω_r, the first derivate of the magnitude of T(jω) is zero.
Differentiate M with respect to u.

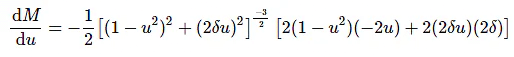
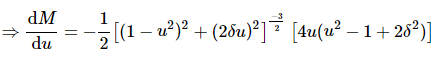
Substitute, u = u_r and dM/du == 0 in the above equation.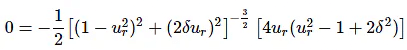

⇒ 4ur(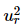−1 + 2δ²) = 0
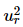⇒ −1 + 2δ² = 0
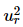⇒  = 1−2δ²

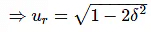
Substitute, u_r = ω_r/ω_n in the above equation.

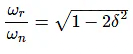
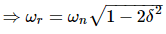
Resonant Peak
It is the peak (maximum) value of the magnitude of T(jω). It is denoted by Mr.
At u = u_r, the Magnitude of T(jω) is -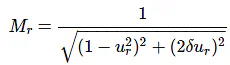

Substitute, 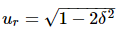and 1−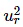=2δ² in the above equation.

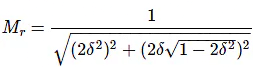
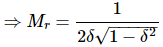
Resonant peak in frequency response corresponds to the peak overshoot in the time domain transient response for certain values of damping ratio δ. So, the resonant peak and peak overshoot are correlated to each other.

Bandwidth
It is the range of frequencies over which, the magnitude of T(jω) drops to 70.7% from its zero frequency value.
At ω=0, the value of u will be zero.
Substitute, u = 0 in M.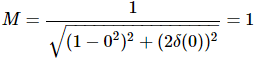

Therefore, the magnitude of T(jω) is one at ω=0.
At 3-dB frequency, the magnitude of T(jω) will be 70.7% of magnitude of T(jω) at ω = 0.
i.e., at ω = ω_B, M = 0.707(1) = 1/√2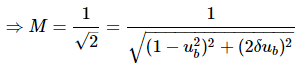


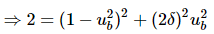
Let, 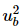= x
⇒ 2 = (1 − x)² + (2δ)²x
⇒ x² + (4δ² − 2)x − 1 = 0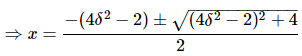

Consider only the positive value of x.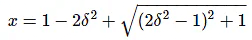


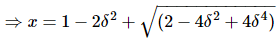
Substitute,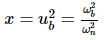

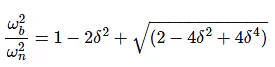
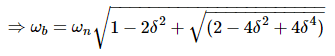
Bandwidth ω_b in the frequency response is inversely proportional to the rise time t_r in the time domain transient response.