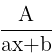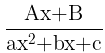Fundamental Formulae for Integration | Physics for JEE Main & Advanced PDF Download
Integration
- Integral Calculus is the branch of calculus where we study integrals and their properties.
- Integration is a very important concept which is the inverse process of differentiation. Both the integral calculus and the differential calculus are related to each other by the fundamental theorem of calculus.
- If we know the f’ of a function that is differentiable in its domain, we can then calculate f. In differential calculus, we used to call f’, the derivative of the function f. Here, in integral calculus, we call f as the anti-derivative or primitive of the function f’. And the process of finding the anti-derivatives is known as anti-differentiation or integration.
- Integration is used to define and calculate the area of the region bounded by the graph of functions.
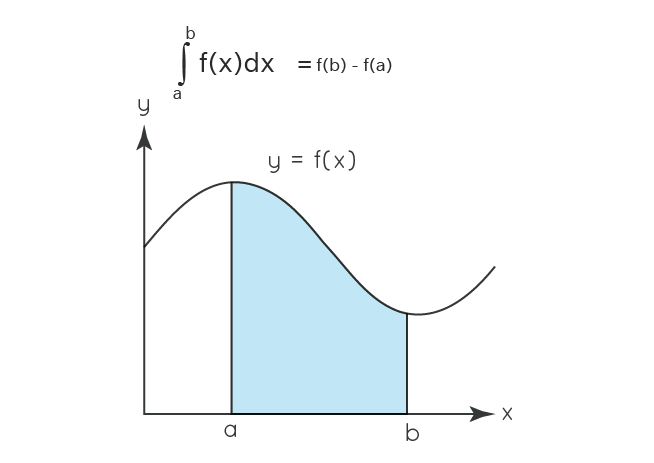 Integration
Integration
Methods of Integration
1. Integration by substitution: In this method the integral ∫f(x)dx is expressed in terms of another integral where some other variables say t is the independent variable; x and t being connected by some suitable relation x=g(t).
It leads to the result ∫f(x)dx=∫f(g(t)). g'(t) dt
2. Integration by parts: This method is used to integrate the product of two functions. If f(x) and g(x) are two integrable functions, then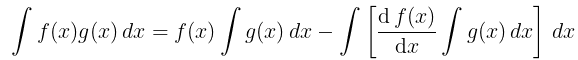
i.e. The integral of (product of two functions) = first function * integral of the second - integral of (derivative of first function * integral of the second function)
In order to select the first function, the following order is followed:
Inverse → Logarithmic → Algebraic → Trigonometric → Exponential
3. Integration by a partial fraction: If the integral is in the form of an algebraic fraction that cannot be integrated then the fraction needs to be decomposed into partial fractions.
Rules for expressing in partial fraction:
- The numerator must be at least one degree less than the denominator.
- For every factor (ax+b) in the denominator, there is a partial fraction

- If a factor is repeated in the denominator n times then that partial fraction should be written n times with degree 1 through n
- For a factor of the form (ax²+bx+c) in the denominator, there will be a partial fraction of the form

Integrals of Rational and Irrational Functions
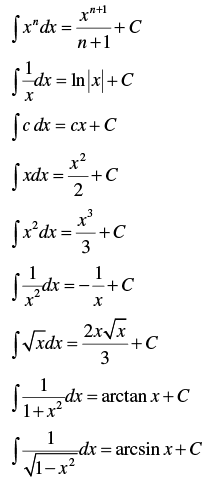
Integrals of Trigonometric Functions
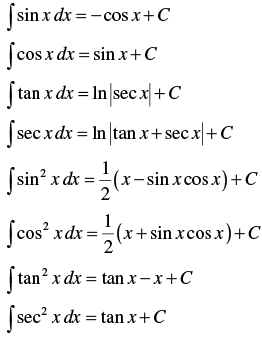
Integrals of Exponential and Logarithmic Functions
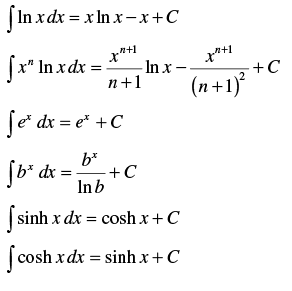
Integrals of Rational Functions
Integrals involving ax + b
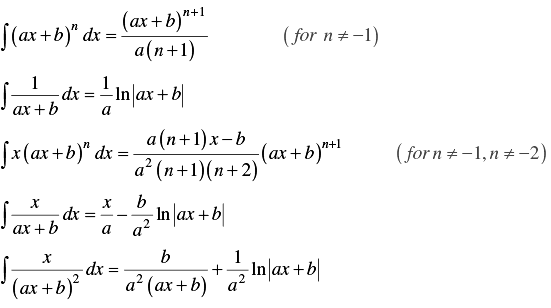
Integral Calculus Examples
Example: Find the integral for the following function.
(i) f(x) = √x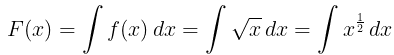
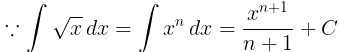
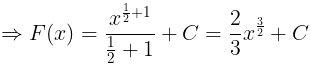
(ii) f(x) =cos2x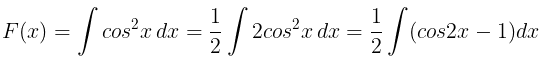
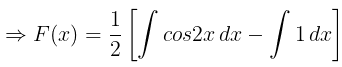
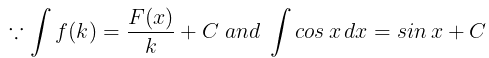
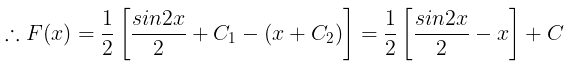
|
291 videos|648 docs|183 tests
|
FAQs on Fundamental Formulae for Integration - Physics for JEE Main & Advanced
| 1. How can we integrate rational functions in calculus? |  |
| 2. What are some common methods used to integrate trigonometric functions? |  |
| 3. How do we integrate exponential and logarithmic functions in calculus? |  |
| 4. What are some fundamental formulae for integration that are commonly used in calculus? |  |
| 5. How can we determine the integral of irrational functions in calculus? |  |