Gauss Theorem, Stokes and Green's Theorem | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| The Divergence Theorem Of Gauss |

|
| Physical demonstration of the divergence theorem |

|
| Stokes’ Theorem |

|
| Green’s Theorem in The Plane |

|
The Divergence Theorem Of Gauss
The divergence theorem of Gauss states that if V is the volume bounded by a closed surface S and A is a vector function of position with continuous derivatives, then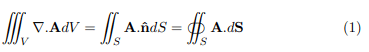
where ˆn is the positive (outward drawn) normal to S. Gauss diveregnce theorem can also be stated as following: The surface integral of the normal component of a vector A taken over a closed surface is equal to the integral of the divergence of A taken over the volume enclosed by the surface.
Proof: Let S be a closed surface which is such that any line parallel to the coordinate axes cuts S in at most two points. Assume the equations of the lower and upper portions, S1 and S2, to be z = f1(x, y) and z = f2(x, y) respectively. Denote the projection of the surface on the xy plane by R.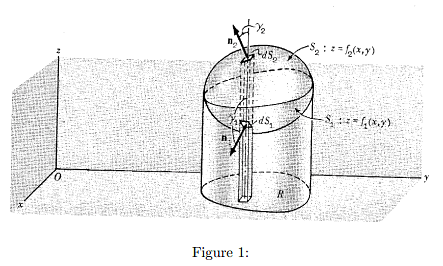 Consider,
Consider,
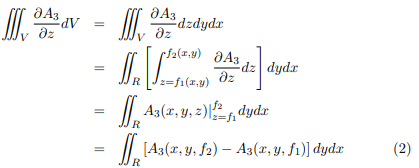 For the upper portion S2, dydx = cos γ2dS2 = k.n2dS2 since the normal n2 to S2 makes an acute angle γ2 with k. For the lower portion S1, dydx = − cos γ1dS2 = k.n1dS1 since the normal n1 to S1 makes an obtuse angle γ1 with k. Then
For the upper portion S2, dydx = cos γ2dS2 = k.n2dS2 since the normal n2 to S2 makes an acute angle γ2 with k. For the lower portion S1, dydx = − cos γ1dS2 = k.n1dS1 since the normal n1 to S1 makes an obtuse angle γ1 with k. Then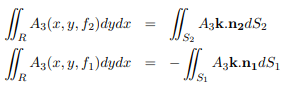
and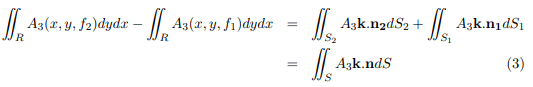 so from equations (2) and (3)
so from equations (2) and (3)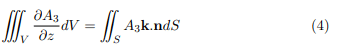
Similarly, by projecting S on the other coordinate planes,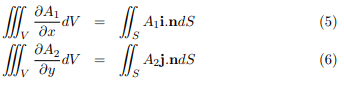 Adding equations (4), (5) and (6),
Adding equations (4), (5) and (6),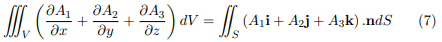 Or
Or Proved.
Proved.
Physical demonstration of the divergence theorem
Let A = velocity v at any point of a moving fluid. From Figure (2 a) below:
Volume of fluid crossing dS in ∆tseconds
= volume contained in cylinder of base dS and slant height v∆t
= (v∆t).ndS = v.ndS∆t
Then, volume per second of fluid crossing dS = v.dS Prom Figure (2 b)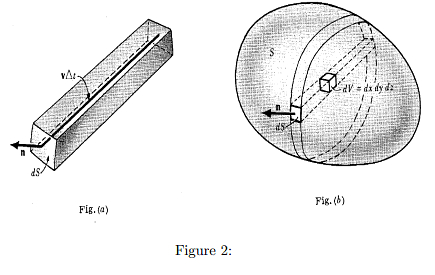
Total volume per second of fluid emerging from closed surface S
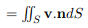
And we know that ∇.vdV is the volume per second of fluid emerging from a volume element dV. Then Total volume per second of fluid emerging from all volume elements in S
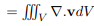
Thus
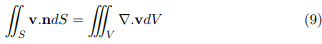
Stokes’ Theorem
Stokes’ theorem states that if S is an open, two-sided surface bounded by a closed, nonintersecting curve C (simple closed curve) then if A has continuous derivatives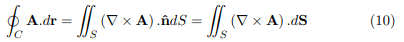
where C is traversed in the positive direction. The direction of C is called positive if an observer, walking on the boundary of S in this direction, with his head pointing in the direction of the positive normal to S, has the surface on his left.
In other words Stokes’ theorem may be stated as following: The line integral of the tangential component of a vector A taken around a simple closed curve C is equal to the surface integral of the normal component of the curl of A taken over any surface S having C as its boundary.
Proof: Let S be a surface which is such that its projections on the xy,
 yz and xz planes are regions bounded by simple closed curves, as indicated in the adjoining figure. Assume S to have representation z = f(x, y) or x = g(y, z) or y = h(x, z), where f, g, h are single-valued, continuous and differentiable functions. We must show that
yz and xz planes are regions bounded by simple closed curves, as indicated in the adjoining figure. Assume S to have representation z = f(x, y) or x = g(y, z) or y = h(x, z), where f, g, h are single-valued, continuous and differentiable functions. We must show that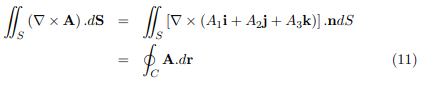
where Cis the boundary of S.
Consider first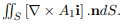
Since
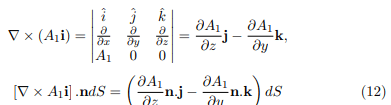
If z = f(x, y) is taken as the equation of S, then the position vector to any point of S is r = xi + yj + zk = xi + yj + f(x, y)k so that 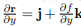 . But ∂r/ ∂y is a vector tangent to S and thus perpendicular to n, so that
. But ∂r/ ∂y is a vector tangent to S and thus perpendicular to n, so that
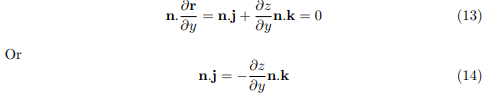
Substituting equation (14) into equation (12), we obtain
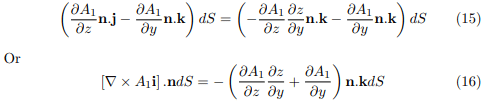
Now on S,1(x, y, z) = A1(x, y, f(x, y)) = F(x, y); hence 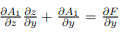 and equation (16) becomes
and equation (16) becomes
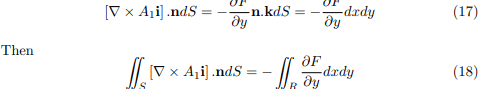
where R is the projection of S on the xy plane. By Green’s theorem for the plane the last integral equals ¸ 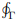 Fdx where Γ is the boundary of R. Since at each point (x, y) of Γ the value of F is the same as the value of A1 at each point (x, y, z) of C, and since dx is the same for both curves, we must have,
Fdx where Γ is the boundary of R. Since at each point (x, y) of Γ the value of F is the same as the value of A1 at each point (x, y, z) of C, and since dx is the same for both curves, we must have,
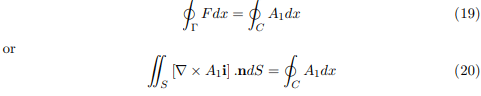
Similarly, by projections on the other coordinate planes,
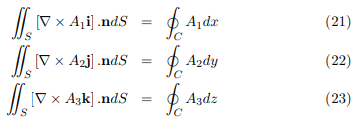
Thus by addition,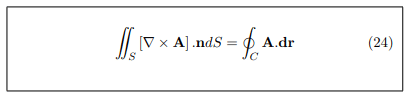 Proved.
Proved.
The theorem is also valid for surfaces S which may not satisfy the restrictions imposed above. For assume that S can be subdivided into surfaces S1, S2, .....Sk with boundaries C1, C2, .....Ck which do satisfy the restrictions. Then Stokes’ theorem holds for each such surface. Adding these surface integrals, the total surface integral over S is obtained. Adding the corresponding line integrals over C1, C2, .....Ck, the line integral over is obtained.
 |
Download the notes
Gauss Theorem, Stokes and Green's Theorem
|
Download as PDF |
Green’s Theorem in The Plane
If R is a closed region of the xy plane bounded by a simple closed curve C and if M and N are continuous functions of x and y having continuous derivatives in R, then
where C is traversed in the positive (counterclockwise) direction. Unless otherwise stated we shall always assume ¸ to mean that the integral is described in the positive sense.
Green’s theorem in the plane is a special case of Stokes’ theorem. Also, it is of interest to notice that Gauss’ divergence theorem is a generalization of Green’s theorem in the plane where the (plane) region R and its closed boundary (curve) C are replaced by a (space) region V and its closed boundary (surface) S. For this reason the divergence theorem is often called Green’s theorem in space.
Green’s theorem in the plane also holds for regions bounded by a finite number of simple closed curves which do not intersect.
Proof: Let the equations of the curves AEB and AFB (see Fig. 4) be 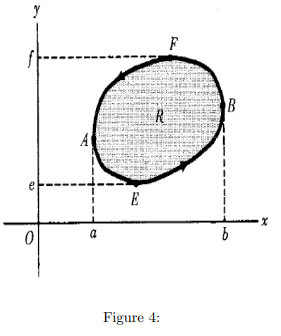
y = Y1(x) and y = Y2(x) respectively. If R is the region bounded by C, we have
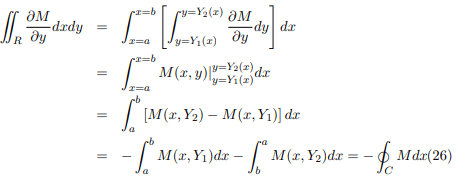
Then,
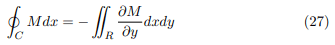
Similarly let the equations of curves EAF and EBF be x = X1(y) and x = X2(y) respectively. Then
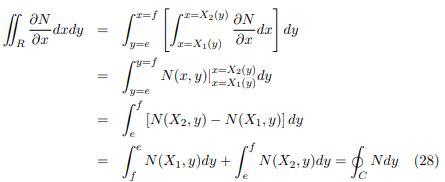
Then,

Adding equations (27) and (29)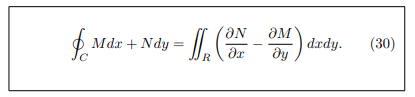
Proved.
|
44 videos|102 docs|58 tests
|
FAQs on Gauss Theorem, Stokes and Green's Theorem - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What is the Divergence Theorem of Gauss? |  |
| 2. How is Stokes' Theorem related to the Divergence Theorem of Gauss? |  |
| 3. What is Green's Theorem in the Plane? |  |
| 4. How are the Divergence Theorem, Stokes' Theorem, and Green's Theorem applied in Mechanical Engineering? |  |
| 5. What are some practical examples where the Divergence Theorem, Stokes' Theorem, and Green's Theorem are used in Mechanical Engineering? |  |


















