JEE Exam > JEE Notes > Mathematics (Maths) for JEE Main & Advanced > General and Middle Terms in the Binomial Theorem
General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced PDF Download
Binomial Theorem Formula – General Term
By the Binomial theorem formula, we know that there are (n + 1) terms in the expansion of (a+b)n. Now, let’s say that T1, T2, T3, T4, … Tn+1 are the first, second, third, fourth, … (n + 1)th terms, respectively in the expansion of (a+b)n. Therefore,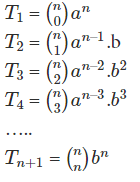
Generalizing it, we have the formula for the general term: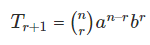
where 0 ≤ r ≤ n. Let’s look at an example now.
Example 1
Find the fourth term in the expansion of (3x–y)7.
Solution. In this example, a = 3x, b = – y, and n = 7. From the above formula, we have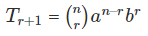
To find the fourth term, T4, r = 3. Therefore,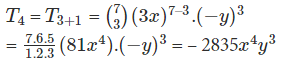
Hence, the fourth term in the expansion of (3x–y)7 = – 2835x4y3
Binomial Theorem Formula – Middle Term
When you are trying to expand (a+b)n and ‘n’ is an even number, then (n + 1) will be an odd number. Which means that the exapnsion will have odd number of terms. In this case, the middle term will be the (n/2 + 1)th term.
For example, if you are expanding (x+y)2, then the middle term will be the (2/2 + 1) = 2nd term. (n/2 + 1)th term is also denoted as (n+2/2)th term.
When you are trying to expand (a+b)n and ‘n’ is an odd number, then (n + 1) will be an even number. Hence, there are two middle terms: (n+1/2)th term and (n+3/2)th term.
For example, if you are expanding (x+y)3, then the middle terms will be, (3+1/2) = 2nd term and (3+3/2) = 3rd term. Let’s look at an example now.
Example 2
Find the middle term/s in the expansion of (x/2 + 3/y)9.
Solution. In this example, since n (= 9) is odd, we have two middle terms namely,
(9+1/2) = 5th term and (9+3/2) = 6th term.
We also have,
a = x/2, b = 3y, and n = 9.
We know that,
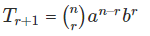
To find the fifth term, T5, r = 4. Therefore,
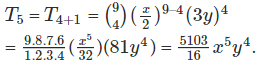
Similarly,
Therefore, the middle terms in the expansion of (x/2 + 3y)9 are 5103/16 x5y4 and 15309/8
x4y5.
More Solved Examples
Question: Find the coefficient of x6 in the expansion of (x+2)9.
Solution: We know that the binomial expansion of (a+b)n is,
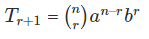
Now, the (r + 1)th term in the expansion of (x+2)9 will be:
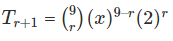
From the above equation, we can deduce that the coefficient of the x-term is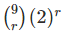 
Next, we need to find the coefficient of x6. Hence,
x6 = (x)9–r
Or, 6 = 9 – r, therefore r = 3.
Using this value of ‘r’,
The coefficient of x6 =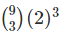 
= 9.8.7/1.2.3.(8) = 672.
The document General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced is a part of the JEE Course Mathematics (Maths) for JEE Main & Advanced.
All you need of JEE at this link: JEE
|
209 videos|443 docs|143 tests
|
FAQs on General and Middle Terms in the Binomial Theorem - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the binomial theorem? |  |
Ans. The binomial theorem is a formula used to expand the powers of binomials. It states that for any positive integer n, the expansion of (a + b)^n can be written as the sum of terms of the form C(n, k) * a^(n-k) * b^k, where C(n, k) represents the binomial coefficient and k ranges from 0 to n.
| 2. What are general terms in the binomial theorem? | |
Ans. The general terms in the binomial theorem refer to the individual terms obtained after expanding a binomial using the binomial theorem formula. These terms follow the pattern C(n, k) * a^(n-k) * b^k, where n represents the power of the binomial, k ranges from 0 to n, and a and b are the coefficients of the binomial.
| 3. What are middle terms in the binomial theorem? | |
Ans. The middle terms in the binomial theorem are the terms that appear in the middle of the expanded binomial when the power n is even. For example, in the expansion of (a + b)^4, the middle terms are the ones that have the power of a and b equal to 2. In general, there are (n+1)/2 middle terms in the expansion when n is even.
| 4. How do you find the binomial coefficient in the binomial theorem? | |
Ans. The binomial coefficient, denoted as C(n, k), represents the number of ways to choose k objects from a set of n objects without considering their order. It can be calculated using the formula C(n, k) = n! / (k! * (n-k)!), where "!" denotes factorial. The binomial coefficient is crucial in determining the coefficients of the terms in the binomial expansion.
| 5. Can the binomial theorem be applied to negative powers of binomials? | |
Ans. Yes, the binomial theorem can be applied to negative powers of binomials. However, to do so, the binomial coefficients must be extended to include negative values. This extension is achieved using the formula C(n, k) = (-1)^k * C(n+k-1, k), where (-1)^k accounts for the alternating signs in the expansion. Applying the binomial theorem to negative powers helps in simplifying complex algebraic expressions.
Related Exams
About this Document
|
4.64/5 Rating |
|
Nov 22, 2024 Last updated |
Document Description: General and Middle Terms in the Binomial Theorem for JEE 2024 is part of Mathematics (Maths) for JEE Main & Advanced preparation.
The notes and questions for General and Middle Terms in the Binomial Theorem have been prepared according to the JEE exam syllabus. Information about General and Middle Terms in the Binomial Theorem covers topics
like and General and Middle Terms in the Binomial Theorem Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for General and Middle Terms in the Binomial Theorem.
Introduction of General and Middle Terms in the Binomial Theorem in English is available as part of our Mathematics (Maths) for JEE Main & Advanced
for JEE & General and Middle Terms in the Binomial Theorem in Hindi for Mathematics (Maths) for JEE Main & Advanced course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced
Description
Full syllabus notes, lecture & questions for General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced - JEE | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) for JEE Main & Advanced | Best notes, free PDF download
Information about General and Middle Terms in the Binomial Theorem
In this doc you can find the meaning of General and Middle Terms in the Binomial Theorem defined & explained in the simplest way possible. Besides explaining types of
General and Middle Terms in the Binomial Theorem theory, EduRev gives you an ample number of questions to practice General and Middle Terms in the Binomial Theorem tests, examples and also practice JEE
tests
|
209 videos|443 docs|143 tests
|
Download as PDF
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
MCQs
,mock tests for examination
,Sample Paper
,Viva Questions
,ppt
,General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced
,shortcuts and tricks
,study material
,Semester Notes
,Free
,video lectures
,Previous Year Questions with Solutions
,General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced
,past year papers
,practice quizzes
,Important questions
,Summary
,Extra Questions
,General and Middle Terms in the Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced
,Objective type Questions
,Exam
;
Additional Information about General and Middle Terms in the Binomial Theorem for JEE Preparation
General and Middle Terms in the Binomial Theorem Free PDF Download
The General and Middle Terms in the Binomial Theorem is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the General and Middle Terms in the Binomial Theorem now and kickstart your journey towards success in the JEE exam.
Importance of General and Middle Terms in the Binomial Theorem
The importance of General and Middle Terms in the Binomial Theorem cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
General and Middle Terms in the Binomial Theorem Notes
General and Middle Terms in the Binomial Theorem Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to General and Middle Terms in the Binomial Theorem.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, General and Middle Terms in the Binomial Theorem Notes on EduRev are your ultimate resource for success.
General and Middle Terms in the Binomial Theorem JEE Questions
The "General and Middle Terms in the Binomial Theorem JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study General and Middle Terms in the Binomial Theorem on the App
Students of JEE can study General and Middle Terms in the Binomial Theorem alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the General and Middle Terms in the Binomial Theorem,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of General and Middle Terms in the Binomial Theorem is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup