Geometric Progression: Introduction & Solved Examples | Quantitative Aptitude (Quant) - CAT PDF Download
Geometric Progression (GP) is a type of sequence where each succeeding term is produced by multiplying each preceding term by a fixed number, which is called a common ratio. This progression is also known as a geometric sequence of numbers that follow a pattern.

- A series in which each preceding term is formed by multiplying it by a constant factor is called a Geometric Progression G. P. The constant factor is called the common ratio and is formed by dividing any term by the term which precedes it.
- In other words, a sequence,
 is called a geometric progression
is called a geometric progression - If
 = constant for all n ∈ N.
= constant for all n ∈ N. - The General form of a G. P. with n terms is a, ar, ar2,…arn -1
Thus if a = the first term
r = the common ratio
Tn = nth term and
Sn = sum of n terms - General term of GP =

Example.1: Find the 9th term and the general term of the progression.
- The given sequence is clearly a G. P. with first term a = 1 and common ratio = r =
Question for Geometric Progression: Introduction & Solved ExamplesTry yourself:How many terms are there in the GP 5, 20, 80, 320, ..........., 20480?
View Solution
Common Ratio of G.P.
Consider the sequence a, ar, ar2, ar3,……
First term = a
Second term = ar
Third term = ar2
Similarly, nth term, tn = arn-1
Thus, the common ratio of geometric progression formula is given as:
Common ratio = (Any term) / (Preceding term)
= tn / tn-1
= (arn – 1 ) /(arn – 2)
= r
Thus, the general term of a GP is given by arn-1 and the general form of a GP is a, ar, ar2,…..
For Example: r = t2 / t1 = ar / a = r
Types of Geometric Progression
Geometric progression can be divided into two types based on the number of terms it has. They are:
- Finite geometric progression (Finite GP)
- Infinite geometric progression (Infinite GP)
(a) Finite Geometric Progression (Finite G.P.)
Suppose a, ar, ar2, ar3,……arn-1 is the given Geometric Progression.
Sum of n terms of a G.P.
The sum of n terms of GP is given by:
Sn = a + ar + ar2 + ar3 +…+ arn-1
The formula to find the sum of n terms of GP is:



Where,
a is the first term
r is the common ratio
n is the number of terms
(b) Infinite geometric progression (Infinite GP)
Terms of an infinite G.P. can be written as a, ar, ar2, ar3, ……arn-1,…….
a, ar, ar2, ar3, ……arn-1,……. is called infinite geometric series.
Sum of Infinite G.P.
The sum of infinite geometric series is given by:
If a G.P. has infinite terms and -1 < r < 1 or |x| < 1, then sum of infinite G.P. is 
Example.2: The inventor of the chess board suggested a reward of one grain of wheat for the first square, 2 grains for the second, 4 grains for the third and so on, doubling the number of the grains for subsequent squares. How many grains would have to be given to inventor? (There are 64 squares in the chess board).
- Required number of grains = 1 + 2 + 22 + 23 + ……. To 64 terms =
Recurring Decimals as Fractions
- If in the decimal representation a number occurs again and again, then we place a dot (.) on the number and read it as that the number is recurring.
- Example: 0.5 (read as decimal 5 recurring).
This mean 0. = 0.55555…….∞
= 0.55555…….∞
0. 4 = 0.477777……∞
= 0.477777……∞
These can be converted into fractions as shown in the example given below
Example.3 Find the value in fractions which is same as of 
Properties of G.P.
- If each term of a GP is multiplied or divided by the same non-zero quantity, then the resulting sequence is also a GP.
Example: For G.P. is 2, 4, 8, 16, 32…
- Selection of terms in G.P.
Sometimes it is required to select a finite number of terms in G.P. It is always convenient if we select the terms in the following manner:
If the product of the numbers is not given, then the numbers are taken as a, ar, ar2, ar3, …. - Three non-zero numbers a, b, c are in G.P. if and only if
b2 = ac or b is called the geometric mean of a & c
b is called the geometric mean of a & c - In a GP, the product of terms equidistant from the beginning and end is always same and equal to the product of first and last terms as shown in the next example.

Geometric Progression Formulas
The list of formulas related to GP is given below which will help in solving different types of problems.
- The general form of terms of a GP is a, ar, ar2, ar3, and so on. Here, a is the first term and r is the common ratio.
- The nth term of a GP is Tn = arn-1
- Common ratio = r = Tn/ Tn-1
- The formula to calculate the sum of the first n terms of a GP is given by:
Sn = a[(rn – 1)/(r – 1)] if r ≠ 1and r > 1
Sn = a[(1 – rn)/(1 – r)] if r ≠ 1 and r < 1 - The nth term from the end of the GP with the last term l and common ratio r = l/ [r(n – 1)].
- The sum of infinite, i.e. the sum of a GP with infinite terms is S∞= a/(1 – r) such that 0 < r < 1.
- If three quantities are in GP, then the middle one is called the geometric mean of the other two terms.
- If a, b and c are three quantities in GP, then and b is the geometric mean of a and c. This can be written as b2 = ac or b =√ac
- Suppose a and r be the first term and common ratio respectively of a finite GP with n terms. Thus, the kth term from the end of the GP will be = arn-k.
Previous Year Question (2022) related to Geometric Mean is discussed below:
Question: The geometric mean radius of a conductor, having four equal strands with each strand of radius ‘𝑟’, as shown in the figure below, is:
(A) 4 𝑟
(B) 1.414 𝑟
(C) 2 𝑟
(D) 1.723 𝑟
Solution: GMR is defined as the effective distance over which self magnetic flux linkages occur
For a solid conductor with radius r,

GMR = r' = 0.7788r
GMR is less than the physical radius of the conductor.
In the given figure, standard conductor with four identical strands touching each other is given with equal radius r.
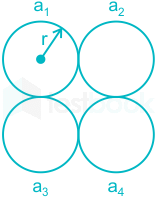
GMRa1 = (r′×2r×2r×22r)1/4
= 1.722 r
Since each strands are identical.
∴ GMR of conductor will be equal to GMR of strand i.e.,
GMRcond = GMRa1
= 1.722 r
Therefore, correct option is (d)
Solved Examples of Geometric Progression
Q.1: If the first term of a G.P. is 20 and the common ratio is 4. Find the 5th term.
Solution: Given,
First term, a = 20
Common ratio, r = 4
We know, Nth term of G.P.,
an = arn-1
⇒ a5 = 20 × 44
= 20 × 256
= 5120
Q.2: The sum of the first three terms of a G.P. is 21/2 and their product is 27. Find the common ratio.
Solution: Let three terms of G.P. be a/r, a, ar.
Given,
Product of first three terms = 27
⇒ (a/r) (a) (ar) = 27
⇒ a3 = 27
⇒ a = 3.
Sum of first three terms = 21/2
⇒ (a / r + a + ar) = 21/2
⇒ a (1 / r + 1 + 1r) = 21/2
⇒ (1 / r + 1 + 1r) = (21/2)/3 = 7/2
⇒ (r2 + r + 1) = (7/2) r
⇒ r2 – (5/2) r + 1 = 0
⇒ r = 2 and ½
Q.3: Find a Geometric Progress for which the sum of first two terms is -4 and the fifth term is 4 times the third term.
Solution: Let the first term of the geometric series be a and the common ratio is r.
Sum of the first two terms = -4
a + ar = -4 ………………(i)
Fifth term is 4 times the third term.
ar4 = 4ar2
r2 = 4
r = ±2
If we consider r = 2, then putting value of r in eq.(i)
a(1+2) = -4
a = -4/3
ar = -8/3
ar2 = -16/3
Thus, the G.P. is -4/3, -8/3, -16/3, …..
Q.4: The number 2048 is which term in the following Geometric sequence 2, 8, 32, 128, . . . . . .
Solution: Here a = 2 and r = 4
nth term G.P is an = arn-1
⇒ 2048 = 2 x ( 4)n-1
⇒ 1024 =( 4)n-1
⇒ ( 4)5 = ( 4) n-1
⇒ n = 6
Q.5: In a G.P, the 6th term is 24 and the 13th term is 3/16 then find the 20th term of the sequence.
Solution: Let first term be ‘a’ and common ratio is ‘r’
Given,
a6 = 24 ————- ( i)
a13 = 3/16 ————– ( ii)
⇒ a6 = a r6-1
a13 = a r13-1
⇒ 24 = a r5
3/16 = a r12
⇒ r7 = 3 / 24 x 16 = 1 / (2)7
⇒ r = 1/2 ———– (iii)
Thus,
⇒ a6 = 24 = a (1/2)5
⇒ a = 3 x 28
Now a20 = a r20-1
a20 = 3 x 28 x ( 1/2 )19 = 3 / 211
Q.6: Find the sum of the geometric series:
4 – 12 + 36 – 108 + ………….. to 10 terms
Solution: The first term of the given Geometric Progression = a = 4 and its common ratio = r = −12/4 = -3.
Sum of the first 10 terms of geometric series:
S10 = a. (rn – 1/r-1)
= 4. ((-3)10 – 1)/(-3-1)
= – (-3)10 – 1
= – 59048
Q.7: ‘x’ and ‘y’ are two numbers whose AM is 25 and GM is 7. Find the numbers.
Solution: Here x’ and ‘y’ are two numbers then
Arithmetic mean = AM = (x+y)/2
25 = (x+y)/2
x+y = 50 ………(i)
Geometric mean, GM = √(xy)
7 = √(xy
72 = xy
xy = 49 ………..(ii)
Solving equation (i) and (ii), we get;
x = 1 and y = 49.
Q.8: Determine the common ratio r of a geometric progression with the first term is 5 and fourth term is 40.
Solution: Given,
First term, a1 = 5
Fourth term, a4 = 40
a4/a1 = 40/5
a1r3/a1 = 40/5
r3 = 8
r = 2
Q.9: If the nth term of a GP is 128 and both the first term a and the common ratio 'r' are 2. Find the number of terms in the GP.
Solution: nth term of a GP, an = 128
First term of GP, a = 2
Common ratio, r = 2
Nth term of G.P., an = a.rn-1
128 = 2.2n-1
64 = 2n-1
26 = 2n-1
n- 1 = 6
n = 7
Therefore, there are 7 terms in GP.
Q.10: What is the sum of infinite geometric series with first term equal to 1 and common ratio is ½?
Solution: By the formula of sum of infinite geometric series, we have;
S = a1. 1/(1 – r)
S = 1. 1/(1-½)
S = 1/(½)
S = 2
Hence, the required sum is 2.
Frequently Asked Questions on Geometric Progression
Answer: The example of GP is: 3, 6, 12, 24, 48, 96,…
Answer: The general form of a Geometric Progression (GP) is given by a, ar, ar2, ar3, ar4,…,arn-1
a = First term
r = common ratio
arn-1 = nth term
ar/a = r
Answer: If the common ratio between each term of a geometric progression is not equal then it is not a GP.
Answer: If a, ar, ar2, ar3,……arn-1 is the given Geometric Progression, then the formula to find sum of GP is:
Sn = a + ar + ar2 + ar3 +…+ arn-1
Or
Sn= a[(rn – 1)/(r – 1)] where r ≠ 1 and r > 1
|
191 videos|133 docs|110 tests
|
FAQs on Geometric Progression: Introduction & Solved Examples - Quantitative Aptitude (Quant) - CAT
| 1. What is the common ratio of a geometric progression? |  |
| 2. What are the types of geometric progressions? |  |
| 3. How can recurring decimals be expressed as fractions using geometric progression? |  |
| 4. What are the properties of a geometric progression? |  |
| 5. What are some common formulas used in geometric progressions? |  |
























