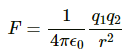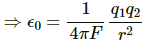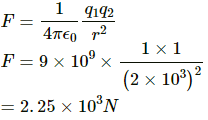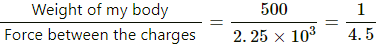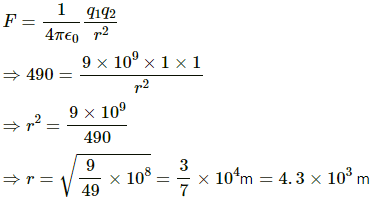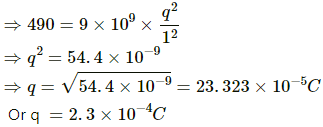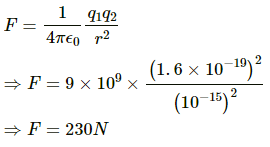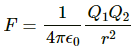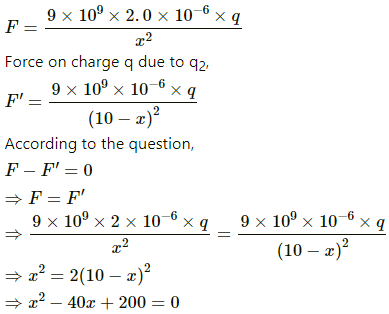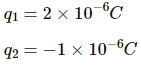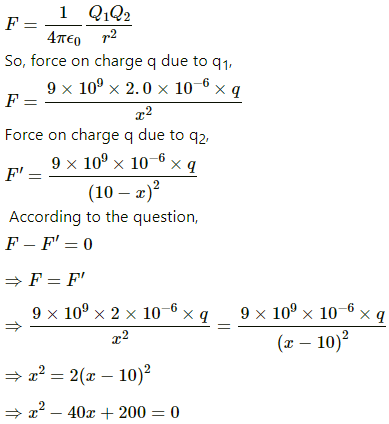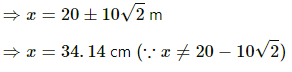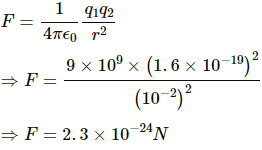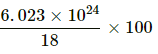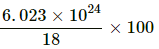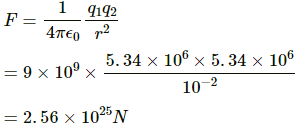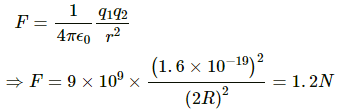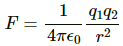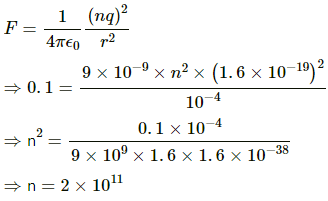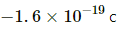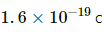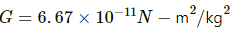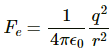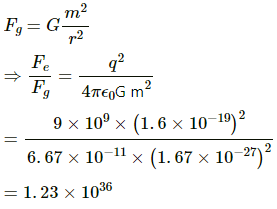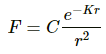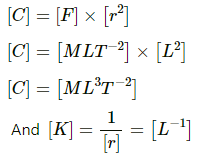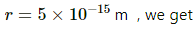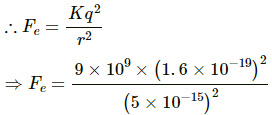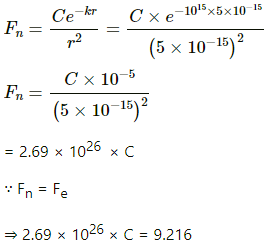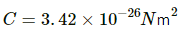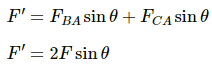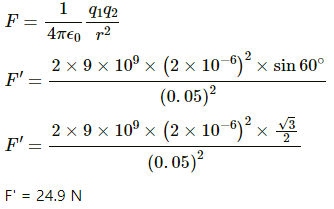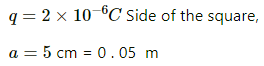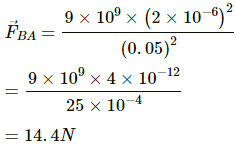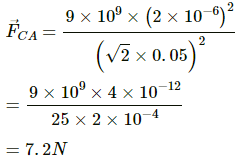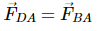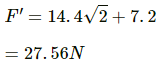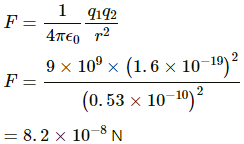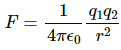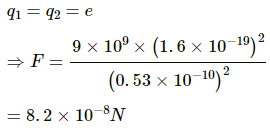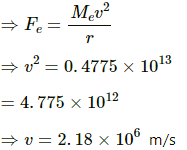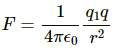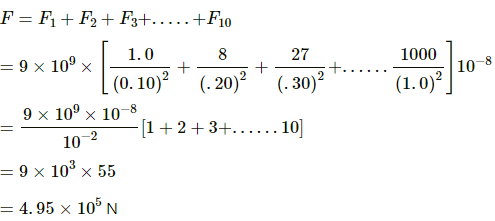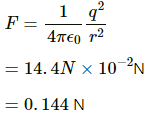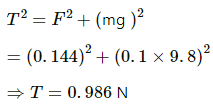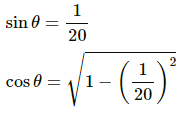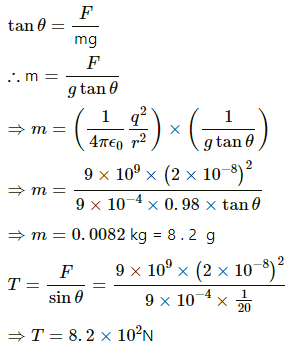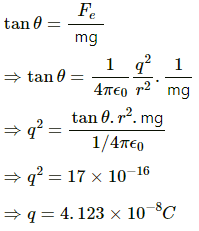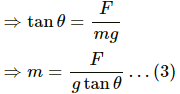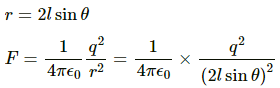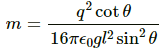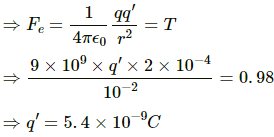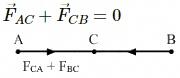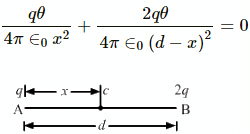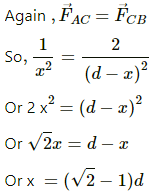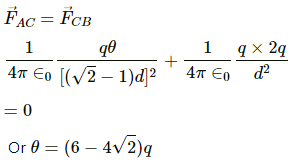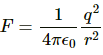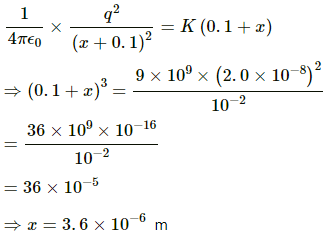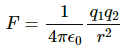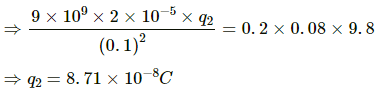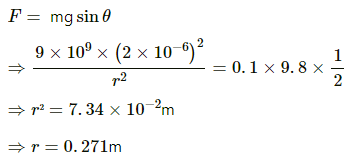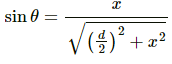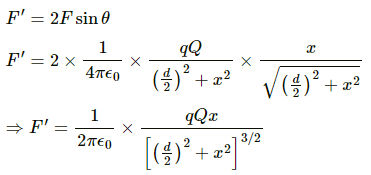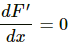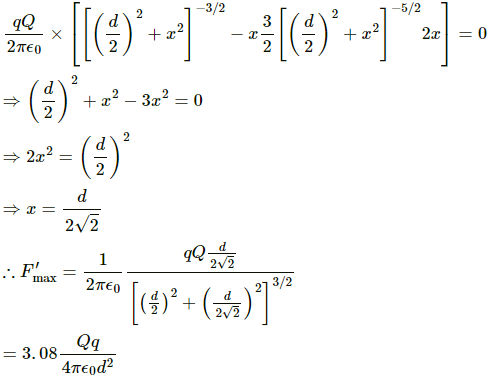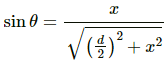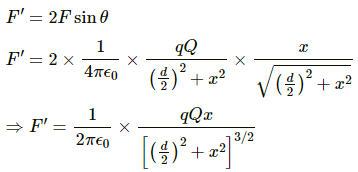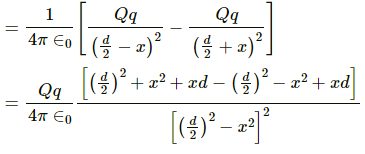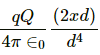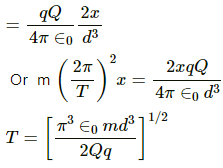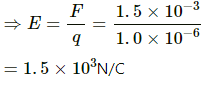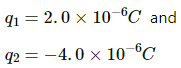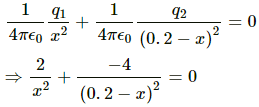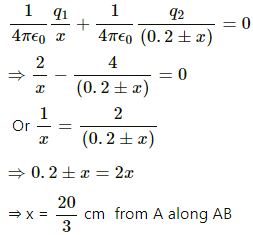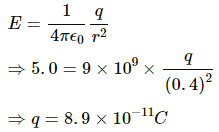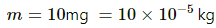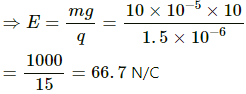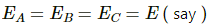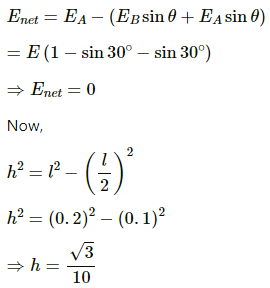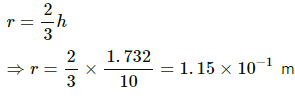HC Verma Questions and Solutions: Chapter 29: Electric Field & Potential- 2 | HC Verma Solutions - JEE PDF Download
Exercises
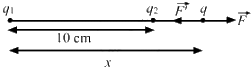
Q.1. Find the dimensional formula of ε0.
By Coulomb's Law,
Using [F] = [MLT−2]
[r] = [M0L1T0]
[q] = [M0L0T1A1], we get
[ε0] = [M−1L−3T4A2]
Q.2. A charge of 1.0 C is placed at the top of your college building and another equal charge at the top of your house. Take the separation between the two charges to be 2.0 km. Find the force exerted by the charges on each other. How many times your weight is this force?
Given:
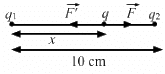
q1 = q2 = q = 1.0 C
Distance between the charges, r = 2 km = 2 × 103 m
By Coulomb's Law, electrostatic force,
Let my mass, m, be 50 kg.
Weight of my body, W = mg
⇒ W = 50 × 10 N = 500 N
Now,
So, the force between the charges is 4.5 times the weight of my body.
Q.3. At what separation should two equal charges, 1.0 C each, be placed, so that the force between them equals the weight of a 50 kg person?
Given:
Magnitude of charges, q1 = q2 = 1 C
Electrostatic force between them, F = Weight of a 50 kg person = mg = 50 × 9.8 = 490 N
Let the required distance be r.
By Coulomb's Law, electrostatic force,
Q.4. Two equal charges are placed at a separation of 1.0 m. What should be the magnitude of the charges, so that the force between them equals the weight of a 50 kg person?
Let the magnitude of each charge be q.
Separation between them, r = 1 m
Force between them, F = 50 × 9.8 = 490 N
By Coulomb's Law force,
Q.5. Find the electric force between two protons separated by a distance of 1 fermi (1 fermi = 10−15 m). The protons in a nucleus remain at a separation of this order.
We know:
Charge on a proton, q = 1.6 × 10−19 C
Given, separation between the charges, r = 10−15 m
By Coulomb's Law, electrostatic force,
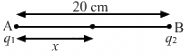
Q.6. Two charges 2.0 × 10−6 C and 1.0 × 10−6 C are placed at a separation of 10 cm. Where should a third charge be placed, such that it experiences no net force due to these charges?
Given:
Let the third charge, q, be placed at a distance of x cm from charge q1, as shown in the figure.
By Coulomb's Law, force,
Force on charge q due to q1,
So, the third charge should be placed at a distance of 5.9 cm from q1.
Q.7. Suppose the second charge in the previous problem is −1.0 × 10−6 C. Locate the position where a third charge will not experience a net force.
Given:
Since both the charges are opposite in nature, the third charge cannot be placed between them. Let the third charge, q, be placed at a distance of x cm from charge q1, as shown in the figure.
By Coulomb's Law, force,
Q.8. Two charged particles are placed 1.0 cm apart. What is the minimum possible magnitude of the electric force acting on each charge?
We know that minimum charge on a body (q) = charge on an electron
⇒ q = 1.6 × 10−19 C
Given:
Separation between the charges, r = 1 cm = 10-2 m
By Coulomb's Law, force,
Q.9. Estimate the number of electrons in 100 g of water. How much is the total negative charge on these electrons?
Molecular mass of water= 18 g
Number of molecules in 18 g of H2O = Avogadro's number
= 6.023 × 1023
Number of electrons in 1 molecule of H2O = (2 × 1) + 8 = 10
Number of electrons in 6.023 × 1023 molecules of H2O = 6.023 × 1024
That is, number of electrons in 18 g of H2O = 6.023 × 1024
So, number of electrons in 100 g of H2O =
= 3.34 × 1025
∴ Total charge = 3.34 × 1025 × 1.6 × 10−19
= 5.34 × 106 C
Q.10. Suppose all the electrons of 100 g water are lumped together to form a negatively-charged particle and all the nuclei are lumped together to form a positively-charged particle. If these two particles are placed 10.0 cm away from each other, find the force of attraction between them. Compare it with your weight.
Molecular mass of water= 18 g
So, number of atoms in 18 g of H2O = Avogadro's number
= 6.023 × 1023
Number of electrons in 1 atom of H2O = (2 × 1) + 8 = 10
Number of electrons in 6.023 × 1023 atoms of H2O = 6.023 × 1024
That is, number of electrons in 18 g of H2O = 6.023 × 1024
So, number of electrons in 100 g of H2O =
= 3.34 × 1025
Total charge = 3.34 × 1025 × (−1.6 × 10−19)
= − 5.34 × 106 C
So total charge of electrons in 100 gm of water, q1 = −5.34 × 106 C
Similarly, total charge of protons in 100 gm of water, q2 = +5.34 × 106 C
Given, r = 10 cm = 0.1 m
By Coulomb's Law, electrostatic force,
This force will be attractive in nature.
Result shows that the electrostatic force is much stronger than the gravitational force between any us and earth (weight = gravitational force between us and earth).
Q.11. Consider a gold nucleus to be a sphere of radius 6.9 fermi in which protons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separation. Why do these protons not fly apart under this repulsion?
Given, radius of the sphere, R = 6.9 fermi
So, the largest separation between two protons = 2R = 13.8 fermi
Charge on a proton, q = 1.6 x 10-19 C
By Coulomb's Law, force of repulsion,
Inside the nucleus, another short-range attractive force (nuclear force) acts on the protons. That's why these protons do not fly apart due to the Coulombian repulsion.
Q.12. Two insulating small spheres are rubbed against each other and placed 1 cm apart. If they attract each other with a force of 0.1 N, how many electrons were transferred from one sphere to the other during rubbing?
Given:
Force of attraction between the spheres, F = 0.1 N
Separation between the spheres, r = 10−2 m
By Coulomb's Law, force,
Let the no. of electrons transferred from one sphere to the other be n. Then,
Q.13. NaCl molecule is bound due to the electric force between the sodium and the chlorine ions when one electron of sodium is transferred to chlorine. Taking the separation between the ions to be 2.75 × 10−8 cm, find the force of attraction between them. State the assumptions (if any) that you have made.
Let the given separation between the ions, i.e. 2.75 × 10−8 cm, be the separation between the transferred electron and the sodium nucleus.
Net charge on thechlorine ion, q1 =
Net charge on the sodium ion, q2 =
By Coulomb's Law, force,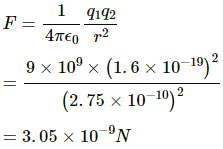
Q.14. Find the ratio of the electrical and gravitational forces between two protons.
We know that the mass of a proton, m = 1.67 × 10−27 kg
Charge on a proton, q = 1.6 × 10−19 C
Gravitational constant,
Electrostatic force,
Gravitational force,
Q.15.1. Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Write down the dimensional formulae and appropriate SI units of C and k.
Given, nuclear force of attraction,
Here e−Kr is just a pure number, i.e. a dimensionless quantity. So,
Q.15.2. Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Suppose that k = 1 fermi−1 and that the repulsive electric force between the protons is just balanced by the attractive nuclear force when the separation is 5 fermi. Find the value of C.
By Coulomb's Law, electric force,
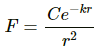
Given , k = 1 fermi-1 = 1015 m
Taking
The electrostatic repulsion between the protons,
= 9.216 N
The strong nuclear force is ,
And nuclear force,` F = Ce−kr/r2
Taking r = 5 × 10-15 m and k = 1 fermi−1, we get
Comparing both the forces, we get
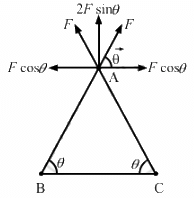
Q.16. Three equal charges, 2.0 × 10−6 C each, are held at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the other two.
Since all the charges are of equal magnitude, the force on the charge at A due to the charges at B and C will be of equal magnitude. (As shown in the figure)
That is,
The horizontal components of force cancel each other and the net force on the charge at A,
Given: r = 5 cm =0.05 m
By Coulomb's Law, force,
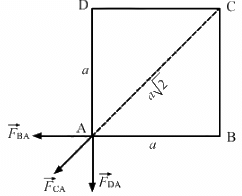
Q.17. Four equal charges of 2.0 × 10−6 C each are fixed at the four corners of a square of side 5 cm. Find the Coulomb's force experienced by one of the charges due to the other three.
Given,
Magnitude of the charges,
By Coulomb's Law, force,
So, force on the charge at A due to the charge at B,
Force on the charge at A due to the charge at C,
Force on the charge at A due to the charge at D,
The resultant force at A, F'=
The resultant force ofwill be
in the direction of
Hence, the resultant force,
Q.18. A hydrogen atom contains one proton and one electron. It may be assumed that the electron revolves in a circle of radius 0.53 angstrom (1 angstrom = 10−10 m and is abbreviated as Å ) with the proton at the centre. The hydrogen atom is said to be in the ground state in this case. Find the magnitude of the electric force between the proton and the electron of a hydrogen atom in its ground state.
Given:
Separation between the two charges, r = 0.53 Å = 0.53 × 10−10 m
q1 = q2 = e
By Coulomb's Law, force,
Q.19. Find the speed of the electron in the ground state of a hydrogen atom. The description of ground state is given in the previous problem.
Given:
Separation between the two charges, r = 0.53 Å = 0.53 × 10−10 m
By Coulomb's Law, force,
Here,
Now, mass of an electron, Me = 9.12 × 10−31 kg
The necessary centripetal force is provided by the Coulombian force.
Q.20. Ten positively-charged particles are kept fixed on the x-axis at points x = 10 cm, 20 cm, 30 cm, ...., 100 cm. the first particle has a charge 1.0 × 10−8 C, the second 8 × 10−8 C, the third 27 × 10−8 C and so on. The tenth particle has a charge 1000 × 10−8 C. Find the magnitude of the electric force acting on a 1 C charge placed at the origin.
By Coulomb's Law, force (F) on charge q due to one charge,
So, net force due to ten charges,
Q.21. Two charged particles with charge 2.0 × 10−8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
Given:
Magnitude of the charges, q = 2.0 × 10−8 C
Separation between the charges, r = 1 m
The tension in the string will be same as the electrostatic force between the charged particles.
So,
T = F
By Coulomb's Law,
Q.22. Two identical balls, each with a charge of 2.00 × 10−7 C and a mass of 100 g, are suspended from a common point by two insulating strings, each 50 cm long. The balls are held 5.0 cm apart and then released. Find (a) the electric force on one of the charged balls (b) the components of the resultant force on it along and perpendicular to the string (c) the tension in the string (d) the acceleration of one of the balls. Answers are to be obtained only for the instant just after the release.
Given:
Magnitude of the charges, q = 2.0 × 10−7 C
Separation between the charges,
r = 5 x 10-2m
Length of the string,
l = 50 cm = 50 x 10-2 m
Mass of the balls, m = 100 g = 0.1 kg
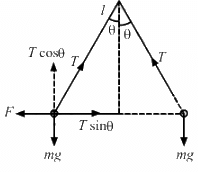
(a) By Coulomb's Law, the electric force,
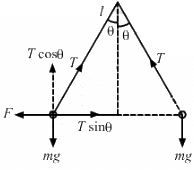
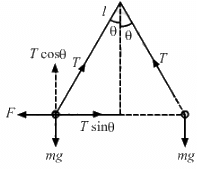
(b) The components of the resultant force along it is zero because mg balances Tcosθ,as shown in the figure. So, F = Tsinθ
(c) Tension in the string,
Tsinθ = F ..(1)
Tcosθ = mg ...(2)
Squaring equations (1) and (2) and adding, we get
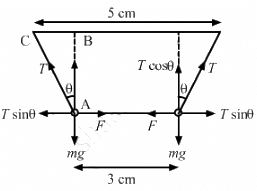
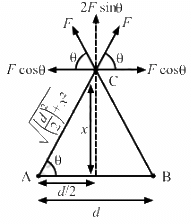
Q.23. Two identical pith balls are charged by rubbing one against the other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 × 10−8 C.
Let the tension in the string be T and the force of attraction between the two balls be F.
From the free-body diagram of the balls, we get
Tcosθ = mg ...(1)
Tsinθ = F ...(2)
From ∆ABC,
From equation (1) and (2),
Q.24. Two small spheres, each with a mass of 20 g, are suspended from a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the separation between the balls at equilibrium is found to be 4 cm. Find the charge on each sphere.
Tcosθ = mg ...(i)
Tsinθ = Fe ...(ii)
Here,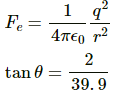
Dividing equation (ii) by (i), we get
Q.25. Two identical pith balls, each carrying a charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
Let the tension in the string be T and force of attraction between the two balls be F.
From the free-body diagram of the ball, we get
Tcos θ = mg ...(1)
Tsin θ = F ...(2)
Here, separation between the two charges,
Substituting the value of F in equation (3), we get
Q.26. A particle with a charge of 2.0 × 10−4 C is placed directly below and at a separation of 10 cm from the bob of a simple pendulum at rest. The mass of the bob is 100 g. What charge should the bob be given so that the string becomes loose?
Given:
Mass of the bob, m = 100 g = 0.1 kg
So, tension in the string, T = mg
⇒ T = 0.1 × 9.8 = 0.98 N
For the tension to be zero, the repelling force (Fe) on the bob = T
Magnitude of the charge placed below the bob, q = 2.0 × 10−4 C
Separation between the charges, r = 0.1 m
When the electrostatic force between the bob and the particle is balanced by the tension in the string then the string will become loose.
Let the required charge on the bob be q' .
Q.27. Two particles A and B with charges q and 2q, respectively, are placed on a smooth table with a separation d. A third particle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table under electrical forces. What should be the charge on C and where should it be clamped?
For equilibrium,
Let the charge at point c be θ.
For a charge at rest,
Q.28. Two identically-charged particles are fastened to the two ends of a spring of spring constant 100 N m−1 and natural length 10 cm. The system rests on a smooth horizontal table. If the charge on each particle is 2.0 × 10−8 C, find the extension in the length of the spring. Assume that the extension is small as compared to the natural length. Justify this assumption after you solve the problem.
Let the extension in the string be x.
Given:
Magnitude of the charges, q = 2.0 × 10−8 C
Separation between the charges, r = (0.1+ x) m
By Coulomb's Law, electrostatic force,
The spring force due to extension x,
F = Kx
For equilibrium,
Electrostatic force = Spring force
Yes, the assumpton is justified. As two similar charges are present at the ends of the spring so they exert repulsive force on each other. Due to the repulsive force between the charges, an extension x is produced in the spring. Springs are made up of elastic material. When a spring is extended then a restoring force acts on it which is always proportioanal to the extension produced and directed opposite to the direction of applied force. The restoring force depends on the elasticity of the material. When the extension is small then only the restoring force is proportinal to the extension. If the extensions camparable to the natural length of the spring then the restoring force will depend on higher powers of the extension produced.
Q.29. A particle A with a charge of 2.0 × 10−6 C is held fixed on a horizontal table. A second charged particle of mass 80 g stays in equilibrium on the table at a distance of 10 cm from the first charge. The coefficient of friction between the table and this second particle is μ = 0.2. Find the range within which the charge of this second particle may lie.
Given:
Magnitude of charge of particle A, q1 = 2.0 × 10−5 C
Separation between the charges, r = 0.1 m
Mass of particle B, m = 80 g = 0.08 kg
Let the magnitude of charge of particle B be q2.
By Coulomb's Law, force on B due to A,
Force of friction on B =μmg
Since B is at equilibrium,
Coulomb force = Frictional force
⇒ F = μmg
∴ The range of the charge = ∓ 8.71×10-8 C
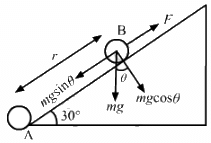
Q.30. A particle A with a charge of 2.0 × 10−6 C and a mass of 100 g is placed at the bottom of a smooth inclined plane of inclination 30°. Where should another particle B, with the same charge and mass, be placed on the incline so that it may remain in equilibrium?
Given:
Magnitude of charge on particles A and B, q = 2.0 × 10−6 C
Mass of particles A and B, m = 100 g = 0.1 kg
Let the separation between the charges be r along the plane.
By Coulomb's Law, force (F) on B due to A,For equilibrium:
For equilibrium along the plane,
So, the charge should be placed at a distance of 27 cm from the bottom.
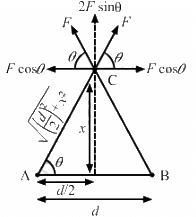
Q.31. Two particles A and B, each with a charge Q, are placed a distance d apart. Where should a particle of charge q be placed on the perpendicular bisector of AB, so that it experiences maximum force? What is the magnitude of this maximum force?
Let the charge q be placed at a distance x on the perpendicular bisector of AB.
As shown in the figure, the horizontal component of force is balanced.
Total vertical component of force,
For maximum force,
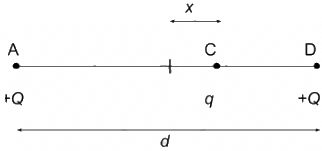
Q.32.1. Two particles A and B, each carrying a charge Q, are held fixed with a separation d between them. A particle C of mass m and charge q is kept at the middle point of the line AB. If it is displaced through a distance x perpendicular to AB, what would be the electric force experienced by it?
The charge q is displaced by a distance x on the perpendicular bisector of AB.
As shown in the figure, the horizontal component of the force is balanced.
Total vertical component of the force,
This is the net electric force experienced by the charge q.
Q.32.2. Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. Assuming x<<d, show that this force is proportional to x.
When x < < d:
Q.32.3. Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. Under what conditions will the particle C execute simple harmonic motion if it is released after such a small displacement? Find the time period of the oscillations if these conditions are satisfied.
For the particle to execute simple harmonic motion:
F' = mw2x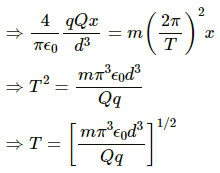
Q.33. Repeat the previous problem if the particle C is displaced through a distance x along the line AB.
Net force
when,
x << d
So, net force =
Q.34. The electric force experienced by a charge of 1.0 × 10−6 C is 1.5 × 10−3 N. Find the magnitude of the electric field at the position of the charge.
Given:
Magnitude of the charges, q = 1.0 × 10−6 C
Electric force, F = 1.5 × 10−3 N
We know that F = qE
Q.35. Two particles A and B possessing charges of +2.00 × 10−6 C and of −4.00 × 10−6 C, respectively, are held fixed at a separation of 20.0 cm. Locate the points (s) on the line AB, where (a) the electric field is zero (b) the electric potential is zero.
Given:
Magnitude of the charges,
Separation between the charges, r = 0.2 m
(a) Let the electric field be zero at a distance x from A, as shown in the figure.
Then,
or x = 48.3 cm from A along BA.
(b) Let the potential be zero at a distance x from A.
and x = 20 cm from A along BA.
Q.36. A point charge produces an electric field of magnitude 5.0 NC−1 at a distance of 40 cm from it. What is the magnitude of the charge?
Given:
Magnitude of the electric field, E = 5.0 NC−1 at a distance, r = 40 cm = 0.4 m
Let the magnitude of the charge be q .
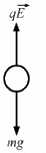
Q.37. A water particle of mass 10.0 mg and with a charge of 1.50 × 10−6 C stays suspended in a room. What is the magnitude of electric field in the room? What is its direction ?
Mass of the particle,
Charge on the particle,
Let the magnitude of the electric field be E.
The particle stays suspended. Therefore,
Downward gravitational force = Upward electric force
That is, mg = qE
The direction of the electric field will be upward to balance the downward gravitational force.
Q.38. Three identical charges, each with a value of 1.0 × 10−8 C, are placed at the corners of an equilateral triangle of side 20 cm. Find the electric field and potential at the centre of the triangle.
Given:
Magnitude of charges, q = 1.0 × 10−8 C
Side of the triangle,
l = 20 cm = 0.2 m
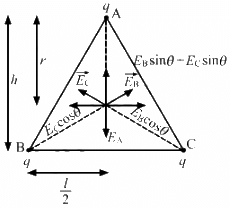
Let EA, EB and EC be the electric fields at the centre due to the charges at A, B and C, respectively.
The distance of the centre is the same from all the charges. So,
Resolving EB and EC into vertical and horizontal components (with θ = 30° )
The horizontal components cancel each other, as shown in the figure.
So, the net electric field at the centre,
Let the distance of the centre from each charge be r.
For an equilateral triangle,
Potential at the centre,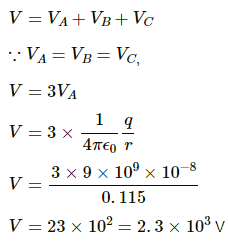
|
134 docs
|