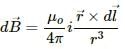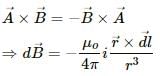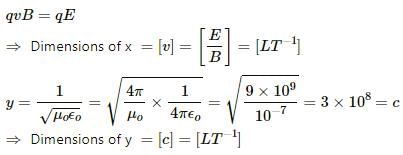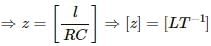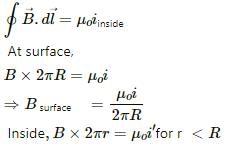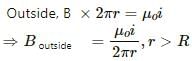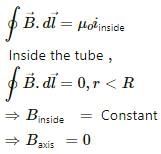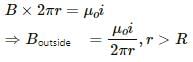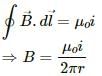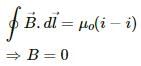Short Answers
Q.1. An electric current flows in a wire from north to south. What will be the direction of the magnetic field due to this wire at a point (a) east of the wire, (b) west of the wire, (c) vertically above the wire and (d) vertically below the wire?
According to the right-hand thumb rule, if the thumb of our right hand points in the direction of the current flowing, then the curling of the fingers will show the direction of the magnetic field developed due to it and vice versa. Let us consider the case where an electric current flows north to south in a wire.
According to the right-hand thumb rule,
(a) for any point in the east of the wire, the magnetic field will come out of the plane of paper
(b) for a point in the west of the wire, the magnetic field will enter the plane of paper
(c) for any point vertically above the wire, the magnetic field will be from right to left
(d) for any point vertically below the wire, the magnetic field will be from left to right
Q.2. The magnetic field due to a long straight wire has been derived in terms of µ, i and d. Express this in terms of ε0, c, i and d.
The magnetic field due to a long, straight wire is given by
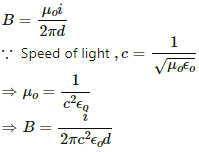
(In terms of ε0, c, i and d)
Q.3. You are facing a circular wire carrying an electric current. The current is clockwise as seen by you. Is the field at the centre coming towards you or going away from you?
According to the right-hand thumb rule, if we curl the fingers of our right hand in the direction of the current flowing, then the thumb will point in the direction of the magnetic field developed due to it and vice versa. Therefore, in this case, the field at the centre is going away from us.
Q.4. In Ampere's  the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
In Ampere's law 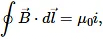 i is the total current crossing the area bounded by the closed curve. The magnetic field B on the left-hand side is the resultant field due to all existing currents.
i is the total current crossing the area bounded by the closed curve. The magnetic field B on the left-hand side is the resultant field due to all existing currents.
Q.5. The magnetic field inside a tightly wound, long solenoid is B = µ0 ni. It suggests that the field does not depend on the total length of the solenoid, and hence if we add more loops at the ends of a solenoid the field should not increase. Explain qualitatively why the extra-added loops do not have a considerable effect on the field inside the solenoid.
The magnetic field due to a long solenoid is given as B = µ0ni, where n is the number of loops per unit length. So, if we add more loops at the ends of the solenoid, there will be an increase in the number of loops and an increase in the length, due to which the ratio n will remain unvaried, thereby leading to not a considerable effect on the field inside the solenoid.
Q.6. A long, straight wire carries a current. Is Ampere's law valid for a loop that does not enclose the wire, or that encloses the wire but is not circular?
Ampere's law is valid for a loop that is not circular. However, it should have some charge distribution in the area enclosed so as to have a constant electric field in the region and a non-zero magnetic field. Even if the loop defined does not have its own charge distribution but has electric influence of some other charge distribution, it can have some constant magnetic field (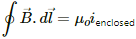 ).
).
Q.7. A straight wire carrying an electric current is placed along the axis of a uniformly charged ring. Will there be a magnetic force on the wire if the ring starts rotating about the wire? If yes, in which direction?
The magnetic force on a wire carrying an electric current i is 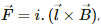 where l is the length of the wire and B is the magnetic field acting on it. If a uniformly charged ring starts rotating around a straight wire, then according to the right-hand thumb rule, the magnetic field due to the ring on the current carrying straight wire placed at its axis will be parallel to it. So, the cross product will be
where l is the length of the wire and B is the magnetic field acting on it. If a uniformly charged ring starts rotating around a straight wire, then according to the right-hand thumb rule, the magnetic field due to the ring on the current carrying straight wire placed at its axis will be parallel to it. So, the cross product will be
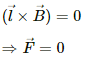
Therefore, no magnetic force will act on the wire.
Q.8. Two wires carrying equal currents i each, are placed perpendicular to each other, just avoiding a contact. If one wire is held fixed and the other is free to move under magnetic forces, what kind of motion will result?
The magnetic force on a wire carrying an electric current i is 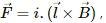 where l is the length of the wire and B is the magnetic field acting on it. Suppose we have one wire in the horizontal direction (fixed) and other wire in the vertical direction (free to move). If the horizontal wire is carrying current from right to left is held fixed perpendicular to the vertical wire, which is free to move, the upper portion of the free wire will tend to move in the left direction and the lower portion of the wire will tend to move in the right direction, according to Fleming's left hand rule, as the magnetic field acting on the wire due to the fixed wire will point into the plane of paper above the wire and come out of the paper below the horizontal wire and the current will flow in upward direction in the free wire. Thus, the free wire will tend to become parallel to the fixed wire so as to experience maximum attractive force.
where l is the length of the wire and B is the magnetic field acting on it. Suppose we have one wire in the horizontal direction (fixed) and other wire in the vertical direction (free to move). If the horizontal wire is carrying current from right to left is held fixed perpendicular to the vertical wire, which is free to move, the upper portion of the free wire will tend to move in the left direction and the lower portion of the wire will tend to move in the right direction, according to Fleming's left hand rule, as the magnetic field acting on the wire due to the fixed wire will point into the plane of paper above the wire and come out of the paper below the horizontal wire and the current will flow in upward direction in the free wire. Thus, the free wire will tend to become parallel to the fixed wire so as to experience maximum attractive force.
Q.9. Two proton beams going in the same direction repel each other whereas two wires carrying currents in the same direction attract each other. Explain.
Two proton beams going in the same direction repel each other, as they are like charges and we know that like charges repel each other.
When a charge is in motion then a magnetic field is associated with it. Two wires carrying currents in the same direction produce their fields (acting on each other) in opposite directions so the resulting magnetic force acting on them is attractive. Due to the magnetic force, these two wires attract each other.
But when a charge is at rest then only an electric field is associated with it and no magnetic fiels is produced by it. So at rest, it repels a like charge by exerting a electric force on it.
Charge in motion can produce both electric field and magnetic field.
The attractive force between two current carrying wires is due to the magnetic field and repulsive force is due to the electric field.
Q.10. In order to have a current in a long wire, it should be connected to a battery or some such device. Can we obtain the magnetic due to a straight, long wire by using Ampere's law without mentioning this other part of the circuit?
We can obtain a magnetic field due to a straight, long wire using Ampere's law by mentioning the current flowing in the wire, without emphasising on the source of the current in the wire. To apply Ampere's circuital law, we need to have a constant current flowing in the wire, irrespective of its source.
Q.11. Quite often, connecting wires carrying currents in opposite directions are twisted together in using electrical appliances. Explain how it avoids unwanted magnetic fields.
Connecting wires carrying currents in opposite directions are twisted together in using electrical appliances. If the wire is twisted, then the resultant fields from consecutive twists are in opposite directions. So the cumulative effect over a long length of wire is roughly zero.
Let at any point in between the two wires, B1 and B2 be the magnetic field due to wire 1 and wire 2 respectively.
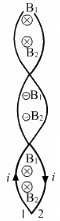
From the diagram, we can see that the net magnetic field due to first turn is into the paper and due to second twisted turn is out of the plane of paper so these fields will cancel each other. Hence if the wire is twisted, then the resultant fields from consecutive twists are in opposite directions. So the cumulative effect over a long length of wire is roughly zero.
Q.12. Two current-carrying wires may attract each other. In absence of other forces, the wires will moves towards each other increasing the kinetic energy. Does it contradict the fact that the magnetic force cannot do any work and hence cannot increase the kinetic energy?
Magnetic field can not do any work and hence can never speed up or down a particle.
Consider 2 wires carrying current in upward direction.
Magnetic field due to current in wire 1 produces a magnetic field out of the plane of paper at the position of wire 2. Due to this magnetic field, a force is exerted on wire 2. Wire 2 electron, moving in downward direction, move in circular paths due to this magnetic force. As these electrons can not come out of the wire so while describing circular path, they hit the edges of the wire and transfer a momentum to the wire. Due to this change in momentum, wire starts moving and gains kinetic energy.
Multiple Choice Questions
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
Explanation
A vertical wire is carrying current in upward direction, so the magnetic field produced will be anticlockwise (according to the right-hand thumb rule). As the electron beam is sent horizontally towards the wire, the direction of the current will be horizontally away from the wire (direction of conventional current is opposite to the direction of the negative charge). According to Fleming's left-hand rule, the force will act in upward direction, deflecting the beam in the same direction.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A current-carrying, straight wire is kept along the axis of a circular loop carrying a current. This straight wire
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A proton beam is going from north to south and an electron beam is going from south to north. Neglecting the earth's magnetic field, the electron beam will be deflected
Explanation
A proton beam is going from north to south, so the direction of the current due to the beam will also be from north to south. Also, an electron beam is going from south to north, so the direction of the current due to the beam will also be from north to south. The direction of conventional current is along the direction of the flow of the positive charge and opposite to the flow of the negative charge. The magnetic field generated due to them will enter the plane of paper in the west and come out of the plane of paper in the east, according to the right-hand thumb rule. Since both the beams have currents in the same direction, they will apply equal and opposite forces on each other and, hence, will attract each other. Thus, the electron beam will be deflected towards the proton beam.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A circular loop is kept in that vertical plane which contains the north-south direction. It carries a current that is towards north at the topmost point. Let A be a point on the axis of the circle to the east of it and B a point on this axis to the west of it. The magnetic field due to the loop
Explanation
According to the right-hand thumb rule, if we curl the fingers of our right hand in the direction of the current flowing, then the stretching of the thumb will show the direction of the magnetic field developed due to it and vice versa.
Let north-south is along x axis and east-west is along y axis. Circular wire is in xz plane. Then point A will lie on positive y axis and B on negative y axis. On looking from point B, current is flowing in anticlockwise direction so the magnetic field will point from right to left. Hence, the magnetic field due to the loop will be towards west at both A and B.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:Consider the situation shown in figure. The straight wire is fixed but the loop can move under magnetic force. The loop will
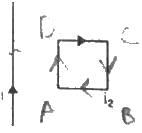
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A charged particle is moved along a magnetic field line. The magnetic force on the particle is
Explanation
The force on a charged particle q moving with velocity v in a magnetic field B is given by
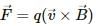
As the charge is moving along the magnetic line of force, the velocity and magnetic field vectors will point in the same direction, making a cross product.
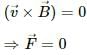
So, the magnetic force on the particle will be zero.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A moving charge produces
Explanation
Because of the presence of a charge, a particle produces an electric field. Also, because of its motion, that is, the flow of charge or current, there is generation of a magnetic field.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A particle is projected in a plane perpendicular to a uniform magnetic field. The area bounded by the path described by the particle is proportional to
Explanation
When a particle of mass m carrying charge q is projected with speed v in a plane perpendicular to a uniform magnetic field B, the field tends to deflect the particle in a circular path of radius r.
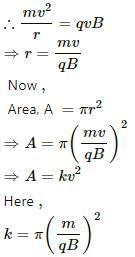
Kinetic energy of the particle,
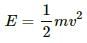
Therefore, the area bounded is proportional to the kinetic energy.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:Two particles X and Y having equal charge, after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is ______.
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
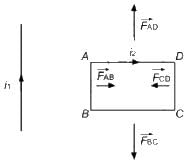
Try yourself:Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carying a current anti parallel to 20 A is placed midway between the two wires. T he magnetic force on it will be
Explanation
According to Fleming's left-hand rule, if the forefinger and middle finger of our left hand point towards the magnetic field acting on a wire and the current flowing in the wire, respectively, then the thumb will point towards the direction in which the force will act (keeping all three perpendicular). Direction of force can be determined using Fleming's left-hand rule.
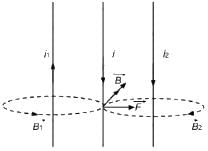
 is the sum is forces acting on the middle wire due to the wires on the both sides of it .
is the sum is forces acting on the middle wire due to the wires on the both sides of it .
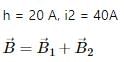
In the figure, dotted circle shows the magnetic filed lines due to both the wires.
Magnetic field at any point on the middle wire will be acting along the tangent to the masgnetic field lines at that point.
Therefore, the wire will experience a magnetic field pointing towards the 40 A wire.
Due to AB, the force will be towards right and due to CD, the force on the wire will be towards right. So, both the forces will add to give a resultant force, which will be towards right, that is, towards the 40 A current-carrying wire.
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
Explanation
Report a problem
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:Consider a long, straight wire of cross-sectional area A carrying a current i. Let there be n free electrons per unit volume. An observer places himself on a trolley moving in the direction opposite to the current with a speed v = i/nAe and separation from the wire by a distance r. The magnetic field seen by the observer is very nearly
Explanation
Magnetic field will be independent of the motion of the observer because the velocity with which the observer is moving is comparable to drift velocity of electron which is very small as compared to the speed of flow of current from one end of wire to other end. So it can be neglected and hence, magnetic field due to the wire w.r.t the observer will be 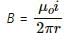
Report a problem
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:The magnetic field at the origin due to a current element 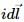 placed at a position
placed at a position 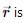
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:Consider three quantities 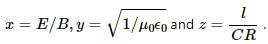 Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
Explanation
Lorentz Force:
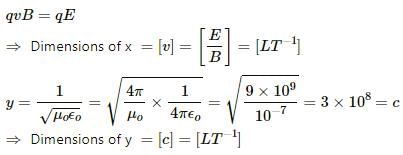
Time constant of RC circuit = RC so dimensionally [RC] = [T]
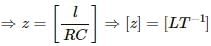
Therefore, x, y and z have the same dimensions.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A long, straight wire carries a current along the z-axis, One can find two points in the x−y plane such that
Explanation
Consider a current carrying wire lying along x axis.
At any two points on z axis which are at equal distance from the wire,one above the wire and one below the wire,the magnitude of magnetic field will be same and their directions will be opposite to each other.
At any two points on z axis which are at different distances from the wire,one above the wire and other also above the wire,the magnitude of magnetic field will be different and their directions will be same to each other.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A long, straight wire of radius R carries a current distributed uniformly over its cross section. T he magnitude of the magnetic field is
Explanation
A long, straight wire of radius R is carrying current i, which is uniformly distributed over its cross section. According to Ampere's law,
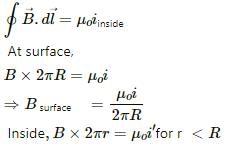
Here i, is the current enclosed by the amperian loop drawn inside the wire.
Binside will be proportional to the distance from the axis.
On the axis
B =0
The magnetic fields from points on the cross section will point in opposite directions and will cancel each other at the centre.
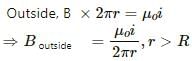
Therefore, the magnitude of the magnetic field is maximum at the surface of the wire and minimum at the axis of the wire.
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A hollow tube is carrying an electric current along its length distributed uniformly over its surface. The magnetic field
Explanation
A hollow tube is carrying uniform electric current along its length, so the current enclosed inside the tube is zero.
According to Ampere's law,
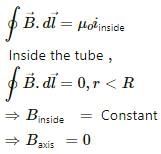
The magnetic fields from points on the circular surface will point in opposite directions and cancel each other.
Outside the tube,
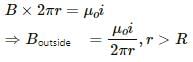
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero
*Multiple options can be correct
Question for HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 1
Try yourself:A steady electric current is flowing through a cylindrical conductor.
Explanation
As the current is flowing through a conductor so it it is distributed only on the surface of the conductor not in the volume of the cylindrical conductor. It is equivalent to charge distribution on a cylindrical sheet for which electric field inside a conducting cylindrical sheet is always zero.
Magnetic fields at any point inside the conducting cylinder is proportional to the distance from the axis of the cylinder.
At the axis, r = 0. This implies that field will be zero at the axis.
 the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve? i is the total current crossing the area bounded by the closed curve. The magnetic field B on the left-hand side is the resultant field due to all existing currents.
).
where l is the length of the wire and B is the magnetic field acting on it. If a uniformly charged ring starts rotating around a straight wire, then according to the right-hand thumb rule, the magnetic field due to the ring on the current carrying straight wire placed at its axis will be parallel to it. So, the cross product will be
where l is the length of the wire and B is the magnetic field acting on it. Suppose we have one wire in the horizontal direction (fixed) and other wire in the vertical direction (free to move). If the horizontal wire is carrying current from right to left is held fixed perpendicular to the vertical wire, which is free to move, the upper portion of the free wire will tend to move in the left direction and the lower portion of the wire will tend to move in the right direction, according to Fleming's left hand rule, as the magnetic field acting on the wire due to the fixed wire will point into the plane of paper above the wire and come out of the paper below the horizontal wire and the current will flow in upward direction in the free wire. Thus, the free wire will tend to become parallel to the fixed wire so as to experience maximum attractive force.

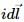 placed at a position
placed at a position 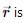
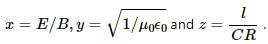 Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.






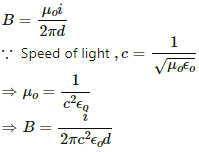
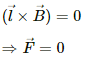
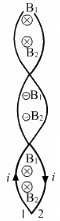
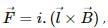 where l is the length of the wire and B is the magnetic field acting on it. If a current-carrying straight wire is kept along the axis of a circular loop carrying current, then according to the right-hand thumb rule, the magnetic field due to the wire on the current-carrying loop will be along its circumference, which contains a current element
where l is the length of the wire and B is the magnetic field acting on it. If a current-carrying straight wire is kept along the axis of a circular loop carrying current, then according to the right-hand thumb rule, the magnetic field due to the wire on the current-carrying loop will be along its circumference, which contains a current element 
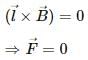
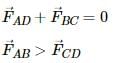
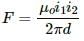
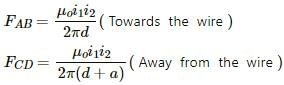
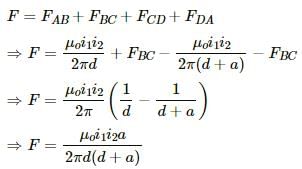
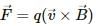
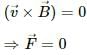
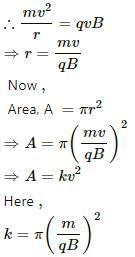
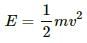
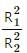
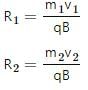
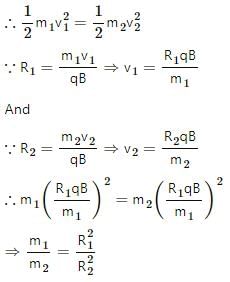

 is the sum is forces acting on the middle wire due to the wires on the both sides of it .
is the sum is forces acting on the middle wire due to the wires on the both sides of it . 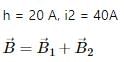
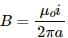 When both the wires carry currents i1 and i2 in the same direction, they produce magnetic fields in opposite directions at any point in between the wires.
When both the wires carry currents i1 and i2 in the same direction, they produce magnetic fields in opposite directions at any point in between the wires.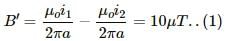
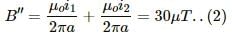

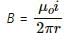
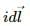 placed at a position
placed at a position 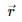 is given by
is given by