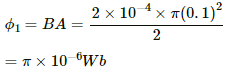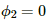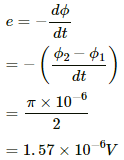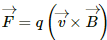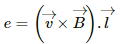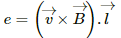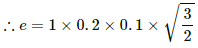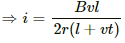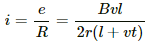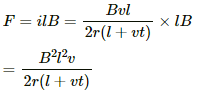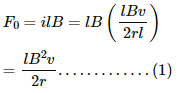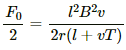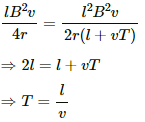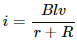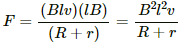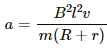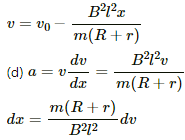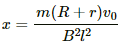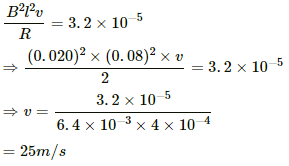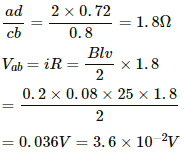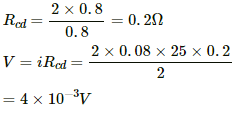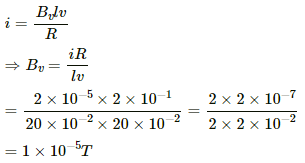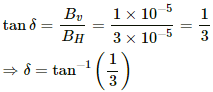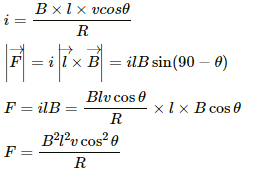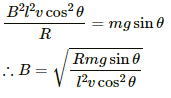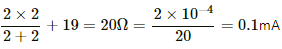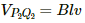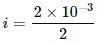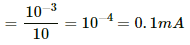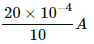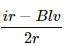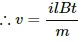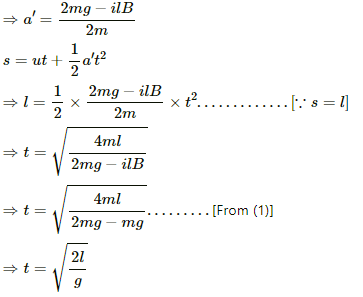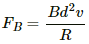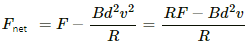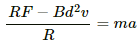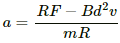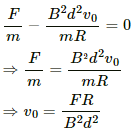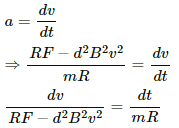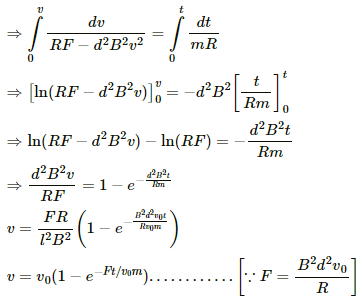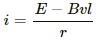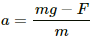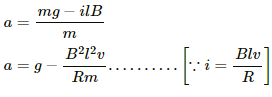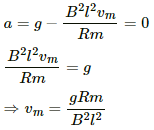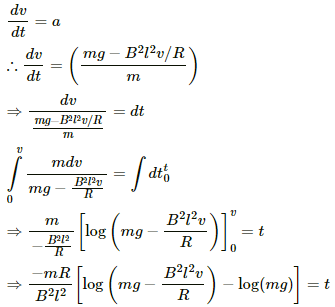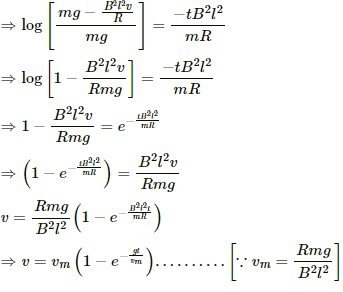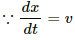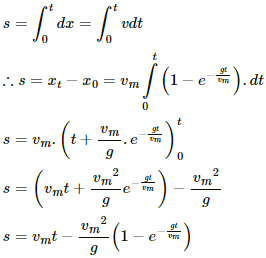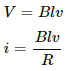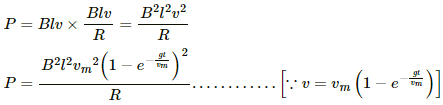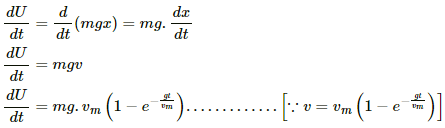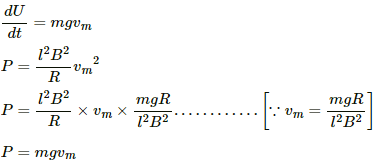HC Verma Questions and Solutions: Chapter 38: Electromagnetic Induction- 3 | HC Verma Solutions - JEE PDF Download

Q. 26. Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.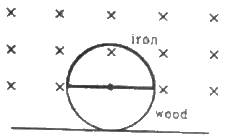

Magnetic flux through the wheel (initially):-

As the wheel rotates, the wooden (non-metal) part of the wheel comes inside the magnetic field and the iron part of the wheel comes outside the magnetic field. Thus, the magnetic flux through the wheel becomes zero.
i.e.
dt = 2 s
The average emf induced in the wheel is given by

Q.27. A 20 cm long conducting rod is set into pure translation with a uniform velocity of 10 cm s⁻¹ perpendicular to its length. A uniform magnetic field of magnitude 0.10 T exists in a direction perpendicular to the plane of motion. (a) Find the average magnetic force on the free electrons of the rod. (b) For what electric field inside the rod, the electric force on a free elctron will balance the magnetic force? How is this electric field created? (c) Find the motional emf between the ends of the rod.

Given:-
Length of the rod, l = 20 cm = 0.2 m
Velocity of the rod, v = 10 cm/s = 0.1 m/s
Magnetic field, B = 0.10 T
(a) The force on a charged particle moving with velocity v in a magnetic field is given by

F = qvB sin θ
Here,
θ = 90°
Now,
F = (1.6 × 10⁻¹⁹) × (1 × 10⁻¹) × (1 × 10⁻¹)
= 1.6 × 10⁻²¹ N
(b) The electrostatic force on the charged particle is qE.
Here,
qE = qvB
⇒ E = (1 × 10⁻¹ ) × (1 × 10⁻¹)
= 1 × 10⁻² V/m
It is created because of the induced emf.
(c) Motional emf between the ends of the rod, e = Bvl
⇒ e = 0.1 × 0.1 × 0.2
= 2 × 10⁻³ V

Q.28. A metallic metre stick moves with a velocity of 2 m s⁻¹ in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick. 

Given:-
Length of the stick, l = 1 m
Magnetic field, B = 0.2 T
Velocity of the stick, v = 2 m/s
Thus, we get
Induced emf, e = Blv = 0.2 × 1 × 2 = 0.4 V

Q.29. A 10 m wide spacecraft moves through the interstellar space at a speed 3 × 10⁷ m s⁻¹. A magnetic field B = 3 × 10⁻¹⁰ T exists in the space in a direction perpendicular to the plane of motion. Treating the spacecraft as a conductor, calculate the emf induced across its width.

Given:-
l = 10 m
v = 3 × 10⁷ m/s
B = 3 × 10⁻¹⁰ T
Now,
Motional emf = Bvl
= (3 × 10⁻¹⁰ ) × (3 × 10⁷ ) × (10)
= 9 × 10⁻²
= 0.09 V

Q.30. The two rails of a railway track, insulated from each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180 km h⁻¹? The vertical component of earth's magnetic field is 0.2 × 10⁻⁴ T and the rails are separated by 1 m.

Here,
Velocity of the train, v = 180 km/h = 50 m/s
Earth's magnetic field, B = 0.2 × 10⁻⁴ T
Separation between the railings, l = 1 m
Induced emf, e = Bvl = 0.2 × 10⁻⁴ × 50 = 10⁻³ V
So, the voltmeter will record 1 mV as the reading. 

Q.31. A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.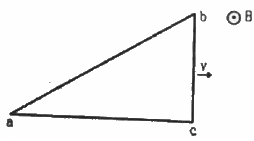

(a) The emf induced in loop abc is zero, as there is no change in the magnetic flux through it.
(b) The emf induced is given by

Emf induced in segment bc, e = Bvl (With positive polarity at point C)
(c) There is no emf induced in segment bc, as the velocity is parallel to its length.
(d) The emf induced in segment ab is calculated by the following formula:-
e = B.v. (Effective length of ab)
The effective length of ab is along the direction perpendicular to its velocity.
Emf induced, e = B.v.(bc)

Q.32. A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular to the diameter joining free ends, (b) the velocity is parallel to this diameter.

(a) The emf induced between the ends of the wire is calculated using the following formula:-
e = Bv (Effective length of the wire)
Effective length of the wire = Component of length perpendicular to the velocity
Here, the component of length moving perpendicular to v is 2r.
∴ Induced emf, e = Bv2r
(b) When the velocity is parallel to the diameter of the semicircular wire, the component of its length perpendicular to its velocity is zero.
∴ Induced emf, e = 0

Q.33. A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s⁻¹.

Given:-
Length of the rod, l = 10 cm = 0.1 m
Angle between the velocity and length of the rod, θ = 60°
Magnetic field, B = 1 T
Velocity of the rod, v = 20 cm/s = 0.2 m/s
The motional emf induced in the rod is given by

∴ e = Bvl sin 60°
We take the component of the length vector that is perpendicular to the velocity vector.

= 17.32 × 10⁻³ V

Q.34. A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?

(a) The maximum value of the emf is between the end points of the diameter perpendicular to the velocity.
The value of the maximum emf is given by
E_max = vB(2R)
(b) The minimum value of emf is between the end points of the diameter parallel to the velocity of the ring.
The minimum value of emf is given by
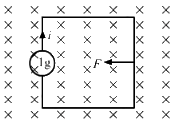
E_min = 0

Q.35. Figure shows a wire sliding on two parallel, conducting rails placed at a separation l. A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity v?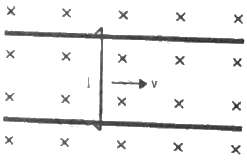

Because the force exerted by the magnetic field on the rod is given by F_magnetic = ilB, the direction of this force is opposite to that of the motion of the rod.
Now, let the external force on it be F.
Because the velocity is constant, the net force acting on the wire must be zero.
Thus, F = F_magnetic = ilB is acting in the direction of the velocity.

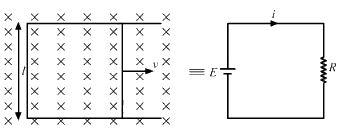
Q.36. Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.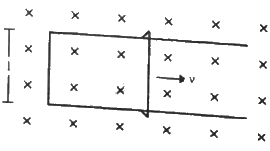

The induced emf is given by
e = Bvl
Total resistance, R = r × Total length of the wire
Because the length of the movable wire is l and the distance travelled by the movable wire in time t is vt, the total length of the loop is 2 (l + vt).
∴ e = i × 2r (l + vt)
Bvl = 2ri (l + vt)

Q.37. Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. (a) Calculate the force needed to keep the sliding wire moving with a constant velocity v. (b) If the force needed just after t = 0 is F₀, find the time at which the force needed will be F₀/2.0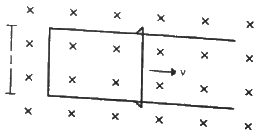

Emf induced in the circuit, e = Bvl
Current in the circuit,

(a) Force F needed to keep the sliding wire moving with a constant velocity v will be equal in magnitude to the magnetic force on it. The direction of force F will be along the direction of motion of the sliding wire.
Thus, the magnitude of force F is given by

(b) The magnitude of force F at t = 0 is given by

Let at time t = T,  the value of the force be F0/2.
Now,

On substituting the value of F₀ from (1), we get

Q.38. Consider the situation shown in figure. The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separated by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangular region and a resistance R connects the rails outside the field region. At t = 0, the wire PQ is pushed towards right with a speed v₀. Find (a) the current in the loop at an instant when the speed of the wire PQ is v, (b) the acceleration of the wire at this instant, (c) the velocity vas a functions of x and (d) the maximum distance the wire will move.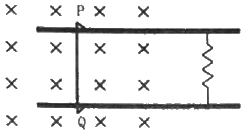

(a) When wire PQ is moving with a speed v, the emf induced across it is given by
e = Blv
Total resistance of the circuit = r + R
∴ Current in the circuit,
(b) Force acting on the wire at the given instant, F = ilB
On substituting the value of i from above, we get

Acceleration of the wire is given by

(c) Velocity can be expressed as:-
(As force is opposite to velocity)
Velocity as the function of x is given by

On integrating both sides, we get

Q.39. A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10⁻⁵N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.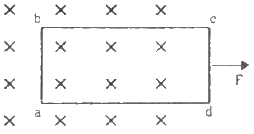

Given:-
Total resistance of the frame, R = 2.0 Ω
Magnetic field, B = 0.020 T
Dimensions of the frame:-
Length, l = 32 cm = 0.32 m
Breadth, b = 8 cm = 0.08 m
(a) Let the velocity of the frame be v.
The emf induced in the rectangular frame is given by
e = Blv
Current in the coil,
i = Blv/R
The magnetic force on the rectangular frame is given by
F = ilB = 3.2 × 10⁻⁵ N
On putting the value of i, we get

(b) Emf induced in the loop, e = vBl
⇒ e = 25 × 0.02 × 0.08
= 4 × 10⁻² V
(c) Resistance per unit length is given by
r = 2/0.8
Ratio of the resistance of part,

(d) Resistance of cd:-

Q.40. Figure shows a metallic wire of resistance 0.20 Ω sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s⁻¹. If the horizontal component of the earth's magnetic field is 3.0 × 10⁻⁵ T, calculate the dip at the place.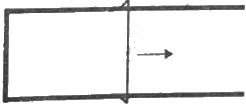

Given:-
Separation between the parallel arms, l = 20 cm = 20 × 10⁻² m
Velocity of the sliding wire, v = 20 cm/s = 20 × 10⁻² m/s
Horizontal component of the earth's magnetic field, B_H = 3 × 10⁻⁵ T
Current through the wire, i = 2 µA = 2 × 10⁻⁶ A
Resistance of the wire, R = 0.2 Ω
Let the vertical component of the earth's magnetic field be Bv and the angle of the dip be δ.
Now,

We know,

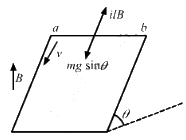
Q.41. A wire ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails joined at the bottom as shown in figure. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the region. If the wire slides on the rails at a constant speed v, show that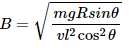

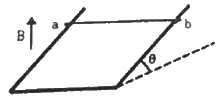
Component of weight along its motion, F' = mgsinθ
The emf induced in the rod due to its motion is given by
e = Bl'v'
Here,
l' = Component of the length of the rod perpendicular to the magnetic field
v' = Component of the velocity of the rod perpendicular to the magnetic field

The direction of force F is opposite to F.'
Because the rod is moving with a constant velocity, the net force on it is zero.
Thus,
F - F' = 0
F = F'
or

Q.42. Consider the situation shown in figure. The wires P₁Q₁ and P₂Q₂ are made to slide on the rails with the same speed 5 cm s⁻¹. Find the electric current in the 19 Ω resistor if (a) both the wires move towards right and (b) if P₁Q₁ moves towards left but P₂Q₂ moves towards right.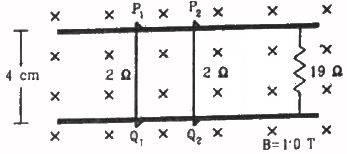

(a) When both wires move in same direction:-
The sliding wires constitute two parallel sources of emf.
The net emf is given by
e = Blv
⇒ e = (1 × 4 × 10⁻² ) × 5 × (10⁻²)
= 20 × 10⁻⁴ V
The resistance of the sliding wires is 2 Ω.
∴ Net resistance =
(b) When both wires move in opposite directions with the same speed, the direction of the emf induced in both of them is opposite. Thus, the net emf is zero.
∴ Net current through 19 Ω = 0

Q.43. Consider the situation shown in figure. The wires P₁Q₁ and P₂Q₂ are made to slide on the rails with the same speed 5 cm s⁻¹. Suppose the 19 Ω resistor is disconnected. Find the current through P₂Q₂ if (a) both the wires move towards right and (b) if P₁Q₁ moves towards left but P₂Q₂ moves towards right.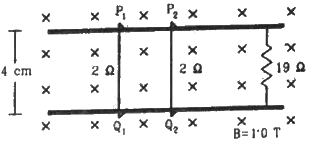

(a) When the wires move in the same direction, their polarity remains the same. The circuit remains incomplete. Therefore, no current flows in the circuit.
(b) When the wires move in opposite directions, their polarities are reversed. Thus, current flows in the circuit.

= 1 × 0.04 × 0.05
= 2 × 10⁻³ V
R = 2 Ω
Current in the circuit is given by

= 1 × 10⁻³ A = 1 mA

Q.44. Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s⁻¹. Find the current in the 10 Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.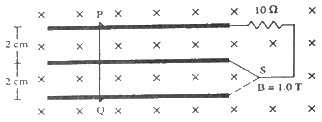

Given:-
Magnetic field, B = 1 T
Velocity of the sliding wire, v = 5 × 10⁻² m/s
Resistance of the connected resistor, R = 10 Ω
(a) When the switch is thrown to the middle rail:-
Length of the sliding wire = 2 × 10⁻² m
Induced emf, E = Bvl
= 1 × (5 × 10⁻²) × (2 × 10⁻²) V
= 10 × 10⁻⁴ = 10⁻³ V
Current in the 10 Ω resistor is given by
i = E/R

(b) When the switch is thrown to the bottom rail:-
The length of the sliding wire becomes 4 × 10⁻² m.
The induced emf is given by
E = Bvl'
= 1 × (5 × 10⁻²) × (4 × 10⁻²)
= 20 × 10⁻⁴ V
Now,
Current, i =
= 2 × 10⁻⁴ A = 0.2 mA

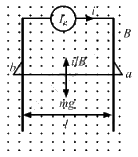
Q.45. The current generator I_g' shown in figure, sends a constant current i through the circuit. The wire cd is fixed and ab is made to slide on the smooth, thick rails with a constant velocity v towards right. Each of these wires has resistance r. Find the current through the wire cd.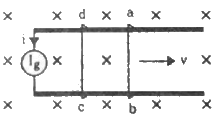

Current passing through the circuit initially = i
Initial emf = ir
Emf induced due to motion of ab, e = Blv
Net emf, e_net= ir − Blv
Net resistance = 2r
Thus, the current passing through the circuit is

Q.46. The current generator I_g' shown in figure, sends a constant current i through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to I_g. The entire system lies in a vertical magnetic field B. Find the velocity of the wire as a function of time.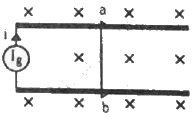

Because current i passes through the sliding wire, the magnetic force on the wire (F) is ilB.
Now,
Acceleration of the sliding wire, a = ilB/m
Velocity of the sliding wire, v = u + at
∵ u = 0

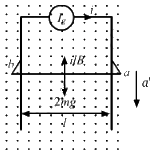
Q.47. The current generator I_g' shown in figure, sends a constant current i through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to I_g. The entire system lies in a vertical magnetic field B. The system is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails (figure). It is found that the wire stays in equilibrium. If the wire ab is replaced by another wire of double its mass, how long will it take in falling through a distance equal to its length?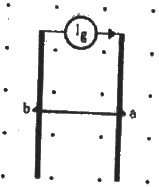

Let us consider the above free body diagram.
As the net force on the wire is zero, ilB = mg.
When the wire is replaced by a wire of double mass, we have

Now, let a' be the acceleration of the wire in downward direction and t be the time taken by the wire to fall.
Net force on the wire = 2mg − ilB = F_net
On applying Newton's second law, we get
2mg − ilB = 2 ma'    ...........(1)

Q.48. The rectangular wire-frame, shown in figure, has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t = 0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. Find this velocity v₀. (c) Show that the velocity at time t is given by v = v₀(1 − e^−Ft/mv0).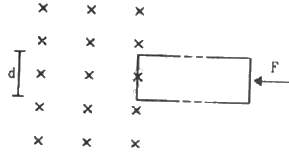

Given:-
Width of rectangular frame = d
Mass of rectangular frame = m
Resistance of the coil = R
(a) As the frame attains the speed v
Emf developed in side AB = Bdv ...........(When it attains a speed v)
Current =Bdv/R
The magnitude of the force on the current carrying conductor moving with speed v in direction perpendicular to the magnetic field as well as to its length is given by
F = ilB
Therefore, Force
As the force is in direction opposite to that of the motion of the frame.
Therefore, Net force is given by
F_net = F - F_B

Applying Newton's second law

Net acceleration is given by
(b) Velocity of the frame becomes constant when its acceleration becomes 0.
Let the velocity of the frame be v₀

As the speed thus calculated depends on F, R, B and d all of them are constant, therefore the velocity is also constant.
Hence, proved that the frame moves with a constant velocity till the whole frame enters.
(c) Let the velocity at time t be v.
The acceleration is given by

Integrating

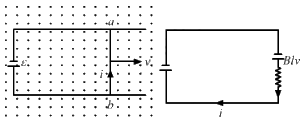
Q.49. Figure shows a smooth pair of thick metallic rails connected across a battery of emf εhaving a negligible internal resistance. A wire ab of length l and resistance r can slide smoothly on the rails. The entire system lies in a horizontal plane and is immersed in a uniform vertical magnetic field B. At an instant t, the wire is given a small velocity vtowards right. (a) Find the current in it at this instant. What is the direction of the current? (b) What is the force acting on the wire at this instant? (c) Show that after some time the wire ab will slide with a constant velocity. Find this velocity.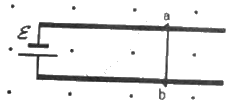

According to Fleming's left hand rule the force in the wire ab will be in the upward direction.
Moreover, a moving wire ab is equivalent to a battery of emf vBl as shown in the figure.

At the given instant, the net emf across the wire (e) is E − Bvl.
(a) The current through the wire is given by

The direction of the current is from b to a.
(b) The force acting on the wire at the given instant is given by
 towards right
(c) The velocity of the wire attains a value such that it satisfies E = Bvl.
The net force on the wire becomes zero. Thus, the wire moves with a constant velocity v.
∴ v = E/Bl

Q.50. A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) What would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity vm. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a function of time. (g) Show that the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.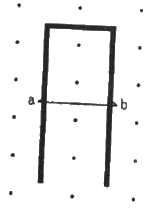

(a) When the speed of the wire is v, the emf developed in the loop is, e = Blv.
(b) Magnitude of the induced current in the wire, I = Blv/R
As wire is moving the magnetic flux passing through the loop is increasing with time. Therefore, the direction of the current should be as such to oppose the change in magnetic flux. Therefore in order to induce the current in anticlockwise direction the current flows from b to a
(c) Due to motion of the wire in the magnetic field there is a force in upward direction (perpendicular to the wire).
The magnitude of the force on the wire carrying current i is given by F = ilB
The net force on the wire = mg - F = mg - ilB
Downward acceleration of the wire due to current,

(d) Let the wire start moving with a constant velocity.
Now,
Let the speed of the wire be v_m
As speed is constant, acceleration, a = 0

(e) The acceleration of the wire can be expressed as time rate of change of velocity


(f) The velocity can be expressed as time rate of change of position x is the position of the wire at instant t.

Thus, the displacement of the wire can be expressed as:-

(g) Rate of development of heat in the wire is given by P = V × i

Therefore, the rate of development of heat in the wire is given by

Rate of decrease in potential energy is given by

After the steady state, i.e., t → ∞,

Thus, after the steady state,
P = dU/dt