HOTS Question Answers: Parallel and Intersecting Lines | Mathematics (Ganita Prakash) Class 7 - New NCERT PDF Download
Q1: A student uses a set square and ruler to draw two lines that are both perpendicular to a base line. A transversal is then drawn such that it forms a 50° angle with the base line. What is the measure of the corresponding angles formed by the transversal with the two perpendicular lines? Explain why the two lines are parallel.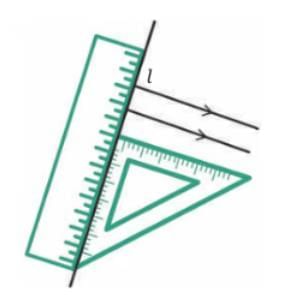
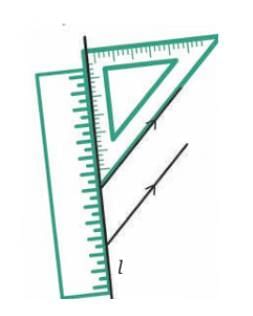
Ans:
The two lines drawn are both perpendicular to the same base line, which means they each make a 90° angle with the base line.
Step 1: Understanding the setup
Since both lines are perpendicular to the base line, they are parallel to each other (because lines perpendicular to the same line are parallel).
A transversal is then drawn, forming a 50° angle with the base line.
Step 2: Finding corresponding angles
The transversal makes a 50° angle with the base line, which means it forms an angle of 50° with one of the parallel lines.
By the corresponding angles rule, the angle it forms with the second parallel line will also be 50°.
Step 3: Explaining why the lines are parallel
Lines that are both perpendicular to the same line are parallel to each other.
Since the transversal forms equal corresponding angles (50°) with both lines, it confirms that the lines are parallel.
Q2: A transversal intersects two parallel lines, creating an angle of 50°. What are the measures of the other seven angles formed? Explain your reasoning using the properties of parallel lines and transversals.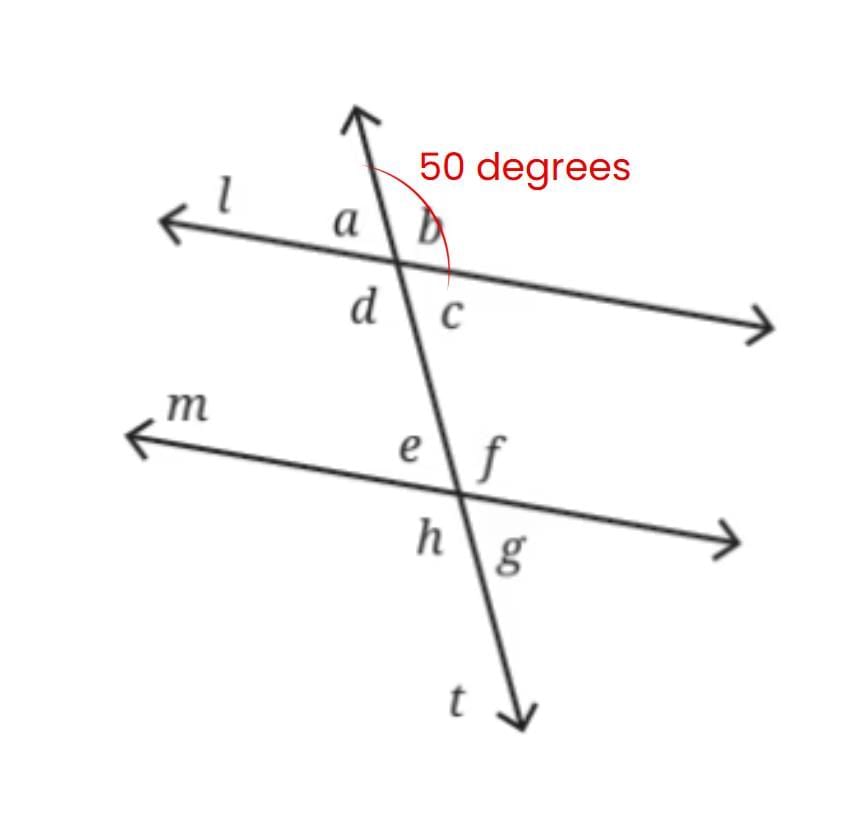
Ans:
When a transversal intersects two parallel lines, it forms 8 angles in total — 4 at each intersection point.
Let’s assume the given angle of 50° is at the top right position of the first intersection.
Step 1: Use the property of Vertically Opposite Angles
Vertically opposite angles are equal.
So, the angle directly across from 50° is also 50°.
Step 2: Use the property of Linear Pair (Supplementary Angles)
Angles on a straight line add up to 180°.
So, the angle adjacent to 50° = 180° − 50° = 130°.
Its vertically opposite angle is also 130°.
Now, we have found all 4 angles at the first intersection:
Two angles of 50°
Two angles of 130°
Step 3: Use the property of Corresponding Angles
Corresponding angles at the second intersection (on the other parallel line) are equal to the ones at the first intersection.
So, the angles at the second intersection will also be:
Two angles of 50°
Two angles of 130°
Q3: Two lines are intersected by a transversal, and one pair of interior angles on the same side of the transversal adds up to 180°. One of the angles is 65°. Find the measures of the corresponding angles to these two angles, and prove the lines are parallel.
Ans:
When two lines are intersected by a transversal, and the interior angles on the same side of the transversal add up to 180°, it is a property that shows the lines are parallel.
Step 1: Find the other angle in the same-side interior pair.
Given one angle = 65°
Sum of same-side interior angles = 180°
Other angle = 180° − 65° = 115°
Step 2: Find the corresponding angles.
The angle corresponding to 65° is also 65° (by corresponding angles rule).
The angle corresponding to 115° is also 115°.
Step 3: Prove the lines are parallel.
Since the same-side interior angles add up to 180°, and
The corresponding angles are equal,
we conclude that the two lines are parallel.
Q4: A transversal intersects two lines, forming a pair of alternate interior angles where one angle is 110°. The other pair of alternate interior angles includes an angle of 70°. Are the two lines parallel? If not, what is the difference between the angles in the second pair of alternate interior angles?
Ans: For two lines to be parallel, the alternate interior angles formed by a transversal must be equal.
In the first pair of alternate interior angles, one angle is 110°.
This means the angle on the opposite side should also be 110° if the lines are parallel.
In the second pair, one of the alternate interior angles is given as 70°.
Since 110° ≠ 70°, the alternate interior angles are not equal, which means the two lines are not parallel.
To find the difference between the angles in the second pair:
One angle = 70°, and if the lines were parallel, the other angle would also be 70°.
But here, since the lines are not parallel and one angle is 70°, the other angle in the pair must be 110° (as given in the opposite pair).
Difference = 110° − 70° = 40°.
Therefore, the lines are not parallel, and the difference between the angles in the second pair of alternate interior angles is 40°.
Q5: In an optical illusion, a student draws 4 horizontal parallel lines on a sheet of paper. Between each pair of lines, they draw zigzag patterns that make the lines appear slanted. If a transversal is drawn across these lines forming a corresponding angle of 120° with the first line, what are the corresponding angles with the other three lines? Why does the illusion make the lines appear non-parallel?
Ans:
Since the four lines are parallel and a transversal crosses all of them, the corresponding angles formed with each line will be the same.
The angle formed with the first line is 120°.
Therefore, the corresponding angles with the other three lines are also 120° each.
This is because corresponding angles are equal when a transversal crosses parallel lines.
The illusion makes the lines appear non-parallel because of the zigzag patterns drawn between the lines. These patterns trick the eyes and brain by creating a false sense of direction and tilt, which causes the parallel lines to appear slanted or not equally spaced. This is a common example of a visual illusion where our perception does not match the actual geometry.
|
41 videos|251 docs|8 tests
|
FAQs on HOTS Question Answers: Parallel and Intersecting Lines - Mathematics (Ganita Prakash) Class 7 - New NCERT
| 1. What are parallel lines, and how can we identify them? |  |
| 2. What are intersecting lines, and what happens when they intersect? |  |
| 3. How do we determine if two lines are perpendicular to each other? |  |
| 4. Can parallel lines ever intersect? Why or why not? |  |
| 5. What are the properties of angles formed by intersecting lines? |  |

















