HOTS Questions: Pair of Linear Equations in Two Variables - Mathematics (Maths) Class 10

Q1. If two of the roots of f(x) = x³ – 5x² – 16x + 80 are equal in magnitude but opposite in sign, then find all of its zeroes.

Hint: Let α and β are the two zeroes which are equal in magnitude but opposite in sign.
∴ α + β = 0
(Let the third zero is γ)
Sum of zeroes of
f(x)= α + β + γ  =
∴ γ = 5  [α + β = 0]
Product of zeroes

∴
⇒ – α² = –16  [α + β = 0 ⇒ β = – α]
⇒ α² = 16   ⇒  α = ± 4
α = ± 4 ⇒ β = ∓ 4    
[∴ β = –α]
Thus, the zeroes are : [± 4, ∓ 4, and 5]

Q2. 
Hint:

Adding (1) and (2), we get x = 1/3 and y = 1/2
Q3. Solve :

Hint: Put x + 2y = p and 2x – y = q
We have      ...(1)
    ...(2)
Solving (1) and (2), we get p = 4 and q = 3
∴ x + 2y = 4  and 2x – y = 3
Solving these equations, we get x = 2 and y = 1

Q4. Solve : x + y = 18 ; y + z  = 12 ;  z + x = 16.
Hint: Adding the three equations, we get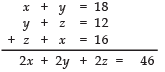

⇒ x + y + z  = 23
Now, (x + y + z = 23) – (x + y = 18)
⇒ z = 5 (x + y + z = 23) – (y + z = 12)
⇒ x = 11 (x + y + z = 23) – (z + x = 16)
⇒ y = 7  
Thus, x = 11, y = 7 and z = 5

Q5. Solve :
Hint: Inverting the equations:

Adding (1), (2) and (3), we get


Now, subtracting (1), (2) and (3) turn by turn from (4), we get x = 2, y = 4 and z = 6

Q6. Solve:
Hint:
From
⇒ 11(x + y – 3) = 2(3x + y) ⇒ 5x + 9y = 33    ...(1)
From
⇒ 11(x + 2y – 4) = 3(3x + y)
⇒ 2x + 9y = 44        ...(2)
Solving (1) and (2), we get x = 3 and y = 2