JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2026 > Revision Notes - Harmonic Progression
Harmonic Progression Class 11 Notes Maths
- Let a, b and c form an H.P. Then 1/a, 1/b and 1/c form an A.P.
- If a, b and c are in H.P. then 2/b = 1/a + 1/c, which can be simplified as b = 2ac/(a+c)
- If ‘a’ and ‘b’ are two non-zero numbers then the sequence a, H, b is a H.P.
- The n numbers H1, H2, ……,Hn are said to be harmonic means between a and b, if a, H1, H2 ……, Hn, b are in H.P. i.e. if 1/a, 1/H1, 1/H2, ..., 1/Hn, 1/b are in A.P. Let d be the common difference of the A.P., Then 1/b = 1/a + (n+1) d ⇒ d = a–b/(n+1)ab.
Thus 1/H1 = 1/a + a–b/(n+1)ab,
1/H2 = 1/a + 2(a–n)/(n+1)ab,
……….. ……….
1/Hn = 1/a + n(a–b)/(n+1)ab. - If x1, x2, … xn are n non-zero numbers, then the harmonic mean ‘H’ of these numbers is given by 1/H = 1/n (1/x1 + 1/ x2 + ……. +1/ xn)
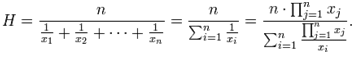
- As the nth term of an A.P is given by an = a + (n-1)d, So the nth term of an H.P is given by 1/ [a + (n -1) d].
- If we have a set of weights w1, w2, …. , wn associated with the set of values x1, x2, …. , xn, then the weighted harmonic mean is defined
- Questions on Harmonic Progression are generally solved by first converting them into those of Arithmetic Progression.
- If ‘a’ and ‘b’ are two positive real numbers then A.M x H.M = G.
- The relation between the three means is defined as A.M > G.M > H.M
- If we need to find three numbers in a H.P. then they should be assumed as 1/a–d, 1/a, 1/a+d
- Four convenient numbers in H.P. are 1/a–3d, 1/a–d, 1/a+d, 1/a+3d
- Five convenient numbers in H.P. are 1/a–2d, 1/a–d, 1/a, 1/a+d, 1/a+2d
The document Harmonic Progression Class 11 Notes Maths is a part of the JEE Course Mock Tests for JEE Main and Advanced 2026.
All you need of JEE at this link: JEE
|
357 docs|100 tests
|
FAQs on Harmonic Progression Class 11 Notes Maths
| 1. What is a harmonic progression? |  |
Ans. A harmonic progression is a sequence of numbers in which the reciprocal of each term is in arithmetic progression. In other words, if the terms of a sequence form an arithmetic progression when their reciprocals are taken, then the original sequence is said to be a harmonic progression.
| 2. How can we determine if a given sequence is a harmonic progression? | |
Ans. To determine if a sequence is a harmonic progression, we need to check if the reciprocals of the terms form an arithmetic progression. If the differences between consecutive reciprocals are constant, then the original sequence is a harmonic progression.
| 3. What is the formula to find the nth term of a harmonic progression? | |
Ans. The formula to find the nth term of a harmonic progression is given by:
an = 1/(a + (n-1)d)
where a is the first term, d is the common difference between the reciprocals of consecutive terms, and n is the term number.
| 4. How can harmonic progression be used in real-life applications? | |
Ans. Harmonic progression has various applications in real-life scenarios. One common application is in calculating the resistance values in electrical circuits. Another application is in music, where harmonic progressions are used to create chords and melodies. Harmonic progression is also used in physics, particularly when studying wave motion and resonance.
| 5. Can a harmonic progression have negative terms? | |
Ans. Yes, a harmonic progression can have negative terms. The terms of a harmonic progression can be positive, negative, or even zero. The important property is that the reciprocals of the terms form an arithmetic progression.
About this Document
4.61/5
Rating
Oct 13, 2025
Last updated
Related Exams
Document Description: Revision Notes - Harmonic Progression for JEE 2025 is part of Mock Tests for JEE Main and Advanced 2026 preparation.
The notes and questions for Revision Notes - Harmonic Progression have been prepared according to the JEE exam syllabus. Information about Revision Notes - Harmonic Progression covers topics
like and Revision Notes - Harmonic Progression Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes - Harmonic Progression.
Introduction of Revision Notes - Harmonic Progression in English is available as part of our Mock Tests for JEE Main and Advanced 2026
for JEE & Revision Notes - Harmonic Progression in Hindi for Mock Tests for JEE Main and Advanced 2026 course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Harmonic Progression Class 11 Notes Maths
Description
Full syllabus notes, lecture & questions for Harmonic Progression Class 11 Notes Maths - JEE | Plus excerises question with solution to help you revise complete syllabus for Mock Tests for JEE Main and Advanced 2026 | Best notes, free PDF download
Information about Revision Notes - Harmonic Progression
In this doc you can find the meaning of Revision Notes - Harmonic Progression defined & explained in the simplest way possible. Besides explaining types of
Revision Notes - Harmonic Progression theory, EduRev gives you an ample number of questions to practice Revision Notes - Harmonic Progression tests, examples and also practice JEE
tests
Related Searches
Sample Paper
,mock tests for examination
,Viva Questions
,Harmonic Progression Class 11 Notes Maths
,Harmonic Progression Class 11 Notes Maths
,Important questions
,Previous Year Questions with Solutions
,Free
,shortcuts and tricks
,Harmonic Progression Class 11 Notes Maths
,study material
,past year papers
,MCQs
,Objective type Questions
,Extra Questions
,Summary
,video lectures
,Semester Notes
,Exam
,practice quizzes
,ppt
;
Additional Information about Revision Notes - Harmonic Progression for JEE Preparation
Revision Notes - Harmonic Progression Free PDF Download
The Revision Notes - Harmonic Progression is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes - Harmonic Progression now and kickstart your journey towards success in the JEE exam.
Importance of Revision Notes - Harmonic Progression
The importance of Revision Notes - Harmonic Progression cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes - Harmonic Progression
Revision Notes - Harmonic Progression Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes - Harmonic Progression.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes - Harmonic Progression Notes on EduRev are your ultimate resource for success.
Revision Notes - Harmonic Progression JEE Questions
The "Revision Notes - Harmonic Progression JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes - Harmonic Progression on the App
Students of JEE can study Revision Notes - Harmonic Progression alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes - Harmonic Progression,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes - Harmonic Progression is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily