Fundamental Theorem of Arithmetic, HCF & LCM | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Fundamental Theorem of Arithmetic |

|
| What are Factors? |

|
| Highest Common Factor (H.C.F) |

|
| Multiples |

|
| Least Common Multiple (L.C.M) |

|
| Co-relation between HCF and LCM |

|
| Applications of LCM and HCF |

|
Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be expressed in the form of primes. In other words, all the natural numbers can be expressed in the form of the product of its prime factors. To recall, prime factors are the numbers that are divisible by 1 and itself only. For example, the number 35 can be written in the form of its prime factors as:
35 = 7 × 5
Here, 7 and 5 are the prime factors of 35
Similarly, another number 114560 can be represented as the product of its prime factors by using the prime factorization method,
114560 = 27 × 5 × 179
So, we have factorized 114560 as the product of the power of its primes.
Therefore, every natural number can be expressed in the form of the product of the power of its primes. This statement is known as the Fundamental Theorem of Arithmetic, unique factorization theorem or the unique-prime-factorization theorem.

Proof for Fundamental Theorem of Arithmetic
In number theory, a composite number is expressed in the form of the product of primes and this factorization is unique apart from the order in which the prime factor occurs.
From this theorem we can also see that not only a composite number can be factorized as the product of their primes but also for each composite number the factorization is unique, not taking into consideration the order of occurrence of the prime factors.
In simple words, there exists only a single way to represent a natural number by the product of prime factors. This fact can also be stated as:
The prime factorization of any natural number is said to be unique for except the order of their factors.
In general, a composite number “a” can be expressed as,
a = p1 p2 p3 ………… pn, where p1, p2, p3 ………… pn are the prime factors of a written in ascending order i.e. p1≤p2≤p3 ………… ≤pn.
Writing the primes in ascending order makes the factorization unique in nature.
Solved Examples
Question: In a formula racing competition the time taken by two racing cars A and B to complete 1 round of the track is 30 minutes and 45 minutes respectively. After how much time will the cars meet again at the starting point?
Solution:
As the time taken by car B is more compared to that of A to complete one round therefore it can be assumed that A will reach early and both the cars will meet again when A has already reached the starting point. This time can be calculated by finding the L.C.M of the time taken by each.
30 = 2 × 3 × 5
45 = 3 × 3 × 5
The L.C.M is 90.
Thus, both cars will meet at the starting point after 90 minutes.
What are Factors?
When a number is said to be a factor of any other second number, then the first number must divide the second number completely without leaving any remainder. In simple words, if a number (dividend) is exactly divisible by any number (divisor), then the divisor is a factor of that dividend.
Example: 4 is a factor of 24 i.e. 4 divides 24 exactly giving 6 as quotient and leaving zero as remainder. Alternatively, 6 is also a factor of 24 as it gives 4 as quotient on division. Therefore, 24 has 1, 24, 4, 6 as its factors in addition to 2, 3, 8 and 12 and all these numbers divide 24 exactly leaving no remainder.
If any natural number has only two factors i.e. 1 and the number itself as its factors, such numbers are called prime numbers.

Highest Common Factor (H.C.F)
The largest or greatest factor common to any two or more given natural numbers is termed as the HCF of given numbers. Also known as GCD (Greatest Common Divisor).
Example: Factors of the number 10 are 1, 2, 5 and 10
Factors of the number 15 are 1, 3, 5 and 15
We can see, the HCF (10, 15) = 5
Methods of Calculating Highest Common Factor
1. Listing all Factors
The simplest method of deriving the HCF is to simply list all the factors of the given number, identify all common factors, and choose the greatest of all the common factors, arriving at your Highest Common Factor(HCF).
Example:
16 = 1, 2, 4, 8, 16
40 = 1, 2, 4, 5, 8, 10, 20, 40
HCF (16,40) = 8 (Because 8 is the largest among all the common factors. Hence, it is the HCF.)
2. Prime Factorization
Given natural numbers are written as the product of prime factors. To obtain the highest common factor multiply all the common prime factors with the lowest degree (power).
Example:
20 = 2 × 2 × 5
12 = 2 × 2 × 3
HCF = 2 × 2 = 4
3. Continued Division
This method is used when we have to find the HCF of relatively larger numbers.
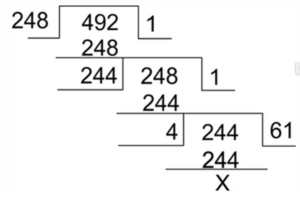
Step 1: Divide the larger number by the smaller number
Step 2: The remainder from Step 1 becomes the divisor, and divisor of Step 1 becomes the dividend.
Step 3: Continue this division process till remainder becomes zero.
Step 4: The divisor of the last division (when remainder is zero) is your HCF.
Finding the Highest Common Factors of Decimals
If the numbers given are decimal numbers, the method of finding HCF is very much similar to the Prime Factorization method, with a little modification.
Example: Say we have to find the HCF of 1.20 and 22.5
First, we convert both numbers to like decimals i.e 1.20 and 22.50
Now we express both numbers, without decimals, as a product of their prime numbers
120 = 2×2×2×3×5
2250 = 2×3×3×5×5×5
So, HCF (120, 2250) = 2×3×5 = 30
Therefore HCF (1.20, 22.5) = 0.30 (taking 2 decimal points)
Finding the Highest Common Factor of Fractions
HCF = HCF of numerators/ LCM of denominators
Example: Say we are to find the HCF of (4/5) and (3/7)
Here the HCF of the numerators 4 and 3 is 1 and the LCM of denominators 5 and 7 is 35.
Therefore the HCF of the two fractions is 1/35.
Solved Examples
Ques: Find the greatest number that divides 167 and 95, leaving 5 as the remainder.
Sol: Although the question sounds complicated, the solution is a simple application of HCF.
The said number divides 167 and leaves 5 as a remainder, So the number divides 162 (167-5) perfectly.
The said number also divides 95 and leaves a remainder of 5, So the number divides 90 (95-5) perfectly.
Therefore the solution is the HCF of 162 and 90, which is 18.
Multiples
A multiple of a number is a number that is the product of a given number and some other natural number. Multiples can be observed in a multiplication table.
Multiples of 2 are as follows:
2 × 1 = 2,
2 × 2 = 4,
2 × 3 = 6,
2 × 4 = 8,
2 × 5 = 10,
2 × 6 = 12,
2 × 7 = 14,
2 × 8 = 16,
and so on.
Least Common Multiple (L.C.M)
Example:
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21….
Multiples of 5 are 5, 10, 15, 20, 25, 30….
LCM (3,5) = 15
Methods of calculating Lowest Common Multiple
This is the simplest method of finding the LCM of any given numbers. You write down several multiples of both the numbers and then identify the smallest common multiple among them.
Example:
Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50….
Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64…..
LCM (5,8) = 40
2. Prime Factorization: Here given natural numbers are written as the product of prime factors. The lowest common multiple will be the product of all the prime factors with the highest degree (power).
Example:
10 = 2×5
12 = 2×2×3
Uncommon Prime Factors = 2,3,5
LCM(10,12) = 2×2×3×5 = 60
3. Long Division Method

Step 1: Write all the numbers in the first row divided by commas
Step 2: We divide the numbers by the lowest and most suitable prime number (should exactly divide at least 2 numbers)
Step 3: Write the quotient of the division in the next row, If the number is not exactly divisible by the prime number, bring it down as it is
Step 4: Continue to do the above steps, till only co-prime numbers are left in the last row.
Step 5: Multiply all prime numbers by which we have divided and all co-prime numbers left in the last row, This is your LCM
Finding the Least Common Multiple of Decimals
We follow the same method of prime factorization, with a few changes
Example:
Let’s say we have to find the LCM of 2.5 and 0.35
First, we convert both numbers to like decimals i.e. 250 and 35
Now we express those two numbers as a product of their prime factors
250 = 2×5×5×5
35 = 5×7
LCM (250,3 5) = 2×5×5×7×5 = 1750
Therefore, LCM of (2.5, 0.35) = 17.50
Solved Examples
Ques: What is the smallest number that when divided by 20 and 48 separately gives the remainder of 7 every time?
Sol: The solution here is an application of the LCM principle. Here firstly we find the LCM of 20 and 48.
20 = 2×2×5
48 = 2×2×2×2×3
LCM (20 ,48) = 2×2×2×2×3×5 = 240
So the required number, that leaves a remainder of 7, is 247 (240+7)
Co-relation between HCF and LCM
So there is an interesting co-relation between H.C.F and L.C.M. of two numbers. The product of the H.C.F. and L.C.M. of any two numbers is always equal to the product of those two numbers. However the same is not applicable to three or more numbers.
LCM (a,b) × HCF (a,b) = (a × b)
Example:
Let the two numbers be 4 and 6.
HCF (4,6) = 2
LCM (4,6) = 12
HCF × LCM = 2 × 12 = 24
Product of the two numbers = 4 × 6 = 24
Applications of LCM and HCF
Now there are various real-life applications of LCM and HCF. The best way to understand these and grasp the concept of LCM and HCF is to learn via examples. So let us take a look at a few examples which will help you understand LCM and HCF.
Example 1: Find the greatest number that will divide 400, 435 and 541 leaving 9, 10 and 14 as remainders respectively.
Sol: The required number would be HCF of (400-9), (435-10) and (541-14)
So the HCF (391,425,527)
391 = 17 × 23
425 = 5 × 5 × 17
527 = 17 × 31
HCF = 17
Therefore the required number is 17.
Example 2: A, B, and C start to jog around a circular stadium. They complete their rounds in 36 seconds, 48 seconds and 42 seconds respectively. After how many seconds will they be together at the starting point?
Sol: The required time is the LCM of all their lap times. This is the earliest when all three will intersect at the same point.
The required time is the LCM (36,48,42)
LCM = 2 × 2 × 3 × 3 × 4 × 7
LCM = 1008
Therefore the required time is 1008 seconds
Example 3: Mr. Das has three classes. Each class has 24, 30 and 18 students respectively. Mr. Das wants to divide each class into groups so that every group in every class has the same number of students and there are no students left over. What is the maximum number of students he can put into each group?
Sol: We have to find the maximum number of students that can be put into each group.
This should give you an indication that here we have to calculate the HCF or GCD.
HFC (24,30,18) = 2 × 3 = 6
Therefore a maximum of 6 students can be put into each group.
Example 4: If the least prime factor of ‘a’ is 3 and the least prime factor of ‘b’ is 7, then find the least prime factor of (a+b)
Sol: When 3 will be the least prime factor of some a number, then 2 will not be a factor of such a number and thus it can be concluded that the number is odd. Thus, a = 2n+1 for some n.
Similarly when 7 will be the least prime factor of another b number, then again 2 will not be a factor of that number and it can be concluded that that number also is odd. Thus b = 2k - 1 for some k.
Adding a + b, we get
= a + b = 2n + 1 + 2k -1
= a + b = 2 (n+k)
a + b is clearly a even number as it is a multiple of 2. Thus, the least prime factor of (a+b) will be clearly 2.
|
127 videos|584 docs|79 tests
|
FAQs on Fundamental Theorem of Arithmetic, HCF & LCM - Mathematics (Maths) Class 10
| 1. What is the Fundamental Theorem of Arithmetic? |  |
| 2. How do you define factors? |  |
| 3. What is the Highest Common Factor (H.C.F)? |  |
| 4. What are multiples? |  |
| 5. How are H.C.F and L.C.M related? |  |





















