Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Important Definitions & Formulas: Some Applications of Trigonometry
Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10 PDF Download
Introduction
In Chapter 9, Class 10 students will learn how to use trigonometry to find the height and distance of objects without measuring them directly. In the past, astronomers relied on trigonometry to calculate distances between planets, Earth, and stars. This chapter explores various ways trigonometry is applied in everyday life.
Topics covered in this chapter include:
- Heights and distances
- The line of sight
- The angle of elevation
- The horizontal line
- The angle of depression
By using trigonometric ratios, we can determine the height or length of an object or the distance between two far-away objects.
Horizontal Level
The horizontal level refers to the straight line that runs through the observer's eye.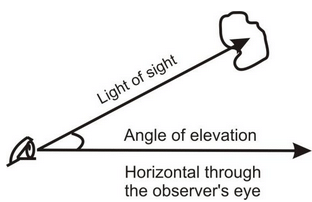
Line of Sight
The line which is drawn from the eyes of the observer to the point being viewed on the object is known as the line of sight.
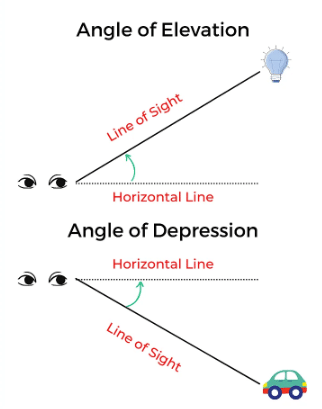
Angle of Elevation
The Angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal when the point being viewed is above the horizontal level, i.e., the case when we raise our head to look at the object.
Angle of Depression
The angle of depression of a point on the object being viewed is the angle formed by the line of sight with the horizontal when the point is below the horizontal level, i.e., the case when we lower our head to look at the point being viewed.
Height and Distance Formulas for Trigonometric ratio
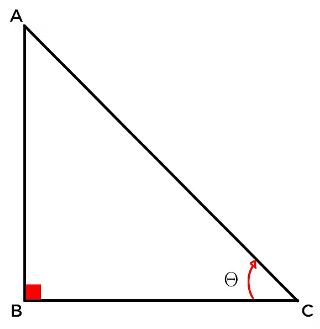
ΔABC is a right-angled triangle where the side AB is the vertical side, AC is the longest side (the hypotenuse), and BC is the horizontal side.
The trigonometric ratios are defined as follows:
- Sin θ = AB/AC
- Cos θ = BC/AC
- Tan θ = AB/BC
- Cosec θ = AC/AB
- Sec θ = AC/BC
- Cot θ = BC/AB
Trigonometrical Identities:
- sin2θ + cos2 θ = 1
- 1 + tan2θ = sec2 θ
- 1 + cot2θ = cosec2 θ
 |
Download the notes
Important Definitions & Formulas: Some Applications of Trigonometry
|
Download as PDF |
Download as PDF
Some Examples Using Above Formulas
Q1: Adam is standing in the Sun. He is 6ft tall and is casting a shadow of 4ft. A flag is also present near the man casting a shadow of 36ft. Calculate the height of the flag.
Ans: The angle of elevation for the Sun will be the same for both the cases.
Therefore, the ratio of object to shadow will be the same for both the cases as per the proportionality rule.
Object height/ Shadow height = 6/ 4 = H /36
Therefore, H = 54 ft = Height of the flag
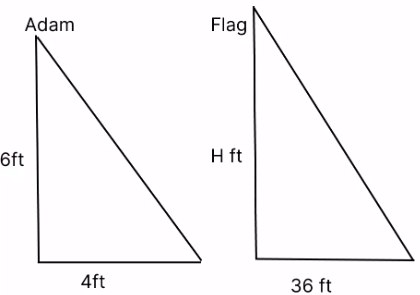
Ans: The angle of elevation for the Sun will be the same for both the cases.
Therefore, the ratio of object to shadow will be the same for both the cases as per the proportionality rule.
Object height/ Shadow height = 6/ 4 = H /36
Therefore, H = 54 ft = Height of the flag
Q2: When a boy looks from the foot and the top of a tower at the roof of a building, the angles of elevation and depression are 27o and 63o, The height of this building is 40m, then calculate the height of the tower given that tan 630 =2.
Ans: Let the tower be AB
Let the building of height 40m be CD
In the given triangle ACD, AC/DC = cot 270
= cot (90-63)
AC/40 = tan 630 = 2
AC = 80m
Now, DE = AC = 80m
Also, in triangle BED, tan 630 = BE/DE
2= BE/80
Therefore, BE = 160 m
Therefore, the height of the tower can be calculated as AE + EB
= 40 +160 = 200m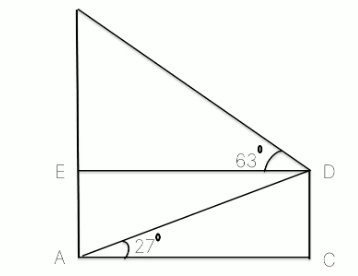
The document Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|550 docs|75 tests
|
FAQs on Important Definitions & Formulas: Some Applications of Trigonometry - Mathematics (Maths) Class 10
| 1. What are the key trigonometric ratios used in height and distance problems? |  |
| 2. How can we calculate the height of a tree using trigonometry? | |
Ans. To calculate the height of a tree using trigonometry, measure the distance from the tree (let's call it \( d \)) and the angle of elevation (\( \theta \)) from the ground to the top of the tree. The height (\( h \)) can be calculated using the formula:
\[ h = d \cdot \tan \theta \]
This formula arises from the tangent ratio, where the height of the tree is the opposite side, and the distance from the tree is the adjacent side.
| 3. What is the formula to find the distance of an object from a point when the angle of depression is known? | |
Ans. When the angle of depression (\( \theta \)) from a point to an object is known, the distance (\( d \)) to the object can be calculated using the formula:
\[ d = h \cdot \tan \theta \]
where \( h \) is the height from which the angle is measured. This is derived from the tangent ratio in the right-angled triangle formed by the height and the distance to the object.
| 4. What role does the angle of elevation play in solving height and distance problems? | |
Ans. The angle of elevation is the angle formed between the horizontal line and the line of sight to an object above the horizontal line. In height and distance problems, it is crucial for determining the height of an object when the distance from the object is known. The relationship can be expressed using the tangent function:
\[ \tan \theta = \frac{\text{Height}}{\text{Distance}} \]
This helps in finding unknown heights by rearranging the formula based on known values.
| 5. Can you explain the relationship between angles of elevation and depression? | |
Ans. The angle of elevation and the angle of depression are related in that they are equal when measured from a horizontal line. The angle of elevation is measured upwards from the horizontal to a point above, while the angle of depression is measured downwards from the horizontal to a point below. In practical problems, if you know the angle of elevation from point A to point B, the angle of depression from point B to point A will be the same, which can be useful in solving height and distance problems.
Related Exams
About this Document
4.84/5
Rating
Mar 26, 2025
Last updated
Document Description: Important Definitions & Formulas: Some Applications of Trigonometry for Class 10 2025 is part of Mathematics (Maths) Class 10 preparation.
The notes and questions for Important Definitions & Formulas: Some Applications of Trigonometry have been prepared according to the Class 10 exam syllabus. Information about Important Definitions & Formulas: Some Applications of Trigonometry covers topics
like Height and Distance Formulas for Trigonometric ratio and Important Definitions & Formulas: Some Applications of Trigonometry Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Definitions & Formulas: Some Applications of Trigonometry.
Introduction of Important Definitions & Formulas: Some Applications of Trigonometry in English is available as part of our Mathematics (Maths) Class 10
for Class 10 & Important Definitions & Formulas: Some Applications of Trigonometry in Hindi for Mathematics (Maths) Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10
Description
Full syllabus notes, lecture & questions for Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Important Definitions & Formulas: Some Applications of Trigonometry
In this doc you can find the meaning of Important Definitions & Formulas: Some Applications of Trigonometry defined & explained in the simplest way possible. Besides explaining types of
Important Definitions & Formulas: Some Applications of Trigonometry theory, EduRev gives you an ample number of questions to practice Important Definitions & Formulas: Some Applications of Trigonometry tests, examples and also practice Class 10
tests
Related Searches
Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10
,Viva Questions
,practice quizzes
,shortcuts and tricks
,Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10
,Extra Questions
,Objective type Questions
,Semester Notes
,mock tests for examination
,Important Definitions & Formulas: Some Applications of Trigonometry | Mathematics (Maths) Class 10
,past year papers
,Important questions
,Free
,Previous Year Questions with Solutions
,video lectures
,Sample Paper
,ppt
,Summary
,MCQs
,Exam
,study material
;
Additional Information about Important Definitions & Formulas: Some Applications of Trigonometry for Class 10 Preparation
Important Definitions & Formulas: Some Applications of Trigonometry Free PDF Download
The Important Definitions & Formulas: Some Applications of Trigonometry is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Definitions & Formulas: Some Applications of Trigonometry now and kickstart your journey towards success in the Class 10 exam.
Importance of Important Definitions & Formulas: Some Applications of Trigonometry
The importance of Important Definitions & Formulas: Some Applications of Trigonometry cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Definitions & Formulas: Some Applications of Trigonometry Notes
Important Definitions & Formulas: Some Applications of Trigonometry Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Definitions & Formulas: Some Applications of Trigonometry.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Definitions & Formulas: Some Applications of Trigonometry Notes on EduRev are your ultimate resource for success.
Important Definitions & Formulas: Some Applications of Trigonometry Class 10 Questions
The "Important Definitions & Formulas: Some Applications of Trigonometry Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Definitions & Formulas: Some Applications of Trigonometry on the App
Students of Class 10 can study Important Definitions & Formulas: Some Applications of Trigonometry alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Definitions & Formulas: Some Applications of Trigonometry,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Definitions & Formulas: Some Applications of Trigonometry is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup