Important Definitions & Formulas: Triangles | Mathematics (Maths) Class 10 PDF Download
Similar figures
Two figures are said to be similar if they have similar shape but size may or may not be equal. As we have studied in class 9 that if both shape and size of both figures are same then they are said to be congruent figures.
Examples of similar figures:
- All squares are similar.
- All circles are similar.
- Every equilateral triangle are similar.
Also, Two polygons with the same number of sides are similar, if
- Their corresponding angles are equal and
- Their corresponding sides are in the same ratio (or proportion).
Remember, The ratio of corresponding sides of a polygon is referred as the scale factor or representative fraction.
Similar Triangles
The same rule which is applied on similarity of polygon is done with it.
Two triangles are similar, if
(i) Their corresponding angles are equal and
(ii) Their corresponding sides are in the same ratio (or proportion).
Geometrically:
∠A = ∠D, ∠B = ∠E, ∠C = ∠F

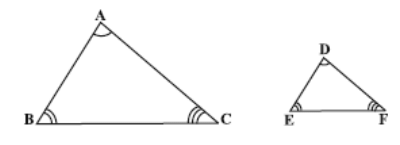
Then the two triangles will be similar.
Basic proportionality Theorem or Thale’s Theorem:
The ratio of any two corresponding sides in two equiangular triangles is always same.
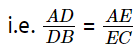
Some Properties related to Similar Triangles
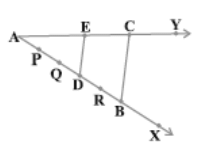
- If a line is drawn parallel to one side of a triangle and it intersects the other two sides at distinct points, the other two sides are divided in the same ratio.
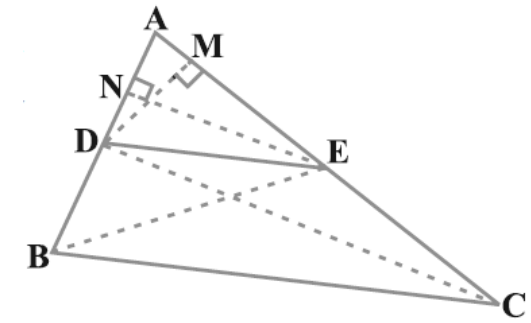
- If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
i.e. DE || BC - If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
- AA similarity rule: If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
- SSS similarity rule: If in two triangles, sides of one triangle are proportional to (e., in the same ratio of ) the sides of another triangle, then their corresponding angles must be equal and hence the two triangles are similar.
- SAS similarity rule: If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
Some examples related to similarity of triangle:
Q1: In the given figure, If PQ || RS, prove that ∆POQ ~ ∆SOR.
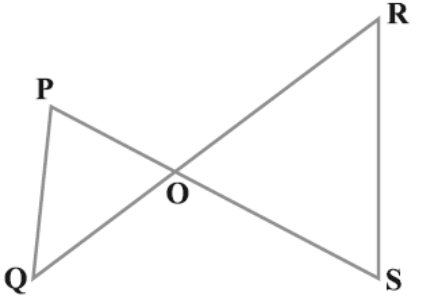
Solution:
PQ || RS (Given)
So, ∠P = ∠S (Alternate angles)
And, ∠Q = ∠R
∠POQ = ∠SOR (Vertically opposite angles)
Thus, ∆POQ ~ ∆SOR (AAA similarity rule)
Q2: In the given figure, if OA .OB = OC .OD. Show that ∠A = ∠C and ∠B = ∠D.
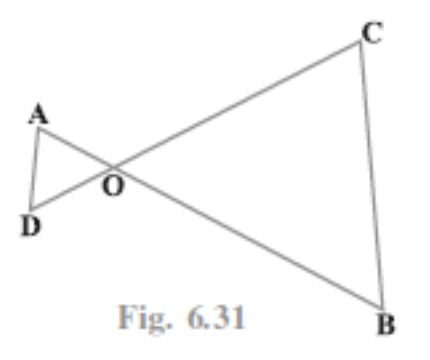 Solution:
Solution:
Given that,
OA .OB = OC .OD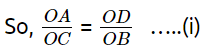
Also, ∠AOD = ∠COB (vertically opposite angles) …..(ii)
From (i) and (ii)
∆AOD ~ ∆COB …. (SAS similarity rule)
Thus, ∠A = ∠C and ∠B = ∠D.
|
127 videos|584 docs|79 tests
|
FAQs on Important Definitions & Formulas: Triangles - Mathematics (Maths) Class 10
Ans. The Basic Proportionality Theorem is also known as Thales Theorem.
2. What is the Converse of Basic Proportionality Theorem?$#
Ans. The Converse of Basic Proportionality Theorem states that if a line divides any two sides of a triangle proportionally, then it is parallel to the third side.
3. What are the criteria for the similarity of triangles?$#
Ans. The criteria for the similarity of triangles include having all angles equal (AAA), having all sides proportional (SSS), and having two angles equal and the included side proportional (SAS).
4. How are similar polygons defined?$#
Ans. Similar polygons are defined as polygons that have the same shape but not necessarily the same size.
5. What are some important definitions and formulas related to triangles?$#
Ans. Some important definitions and formulas related to triangles include the Pythagorean Theorem, the Law of Sines, the Law of Cosines, and the area formulas for different types of triangles.

















