Important Inverse Trigonometric Functions Formulas for JEE and NEET
| Table of contents |

|
| 1. Definition (s) |

|
| 2. Principal Values and Domains of Inverse Circular Functions : |

|
| 3. Properties of Inverse Circular Functions: |

|
| Inverse Trigonometric Functions: |

|
1. Definition (s)
sin−1 x , cos−1 x , tan−1 x etc. denote angles or real numbers whose sine is x, whose cosine is x and whose tangent is x, provided that the answers given are numerically smallest available. These are also written as arc sinx, arc cosx etc .
If there are two angles one positive & the other negative having same numerical value, then positive angle should be taken.
2. Principal Values and Domains of Inverse Circular Functions :
(i) y = sin−1 x where −1 ≤ x ≤ 1 ; 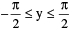 and sin y = x.
and sin y = x.
(ii) y = cos−1 x where −1 ≤ x ≤ 1 ; 0 ≤ y ≤ π and cos y = x.
(iii) y = tan−1 x where x ∈ R; 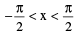 and tan y = x.
and tan y = x.
(iv) y = cosec−1 x where x ≤ −1 or x ≥ 1 ; 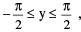 y ≠ 0 and cosec y = x
y ≠ 0 and cosec y = x
(v) y = sec−1 x where x ≤ −1 or x ≥ 1 ; 0 ≤ y ≤ π ; y ≠ π/2 and sec y = x.
(vi) y = cot−1 x where x ∈ R , 0 < y < π and cot y = x.
NOTE THAT : (a) 1st quadrant is common to all the inverse functions.
(b) 3rd quadrant is not used in inverse functions.
(c) 4th quadrant is used in the CLOCKWISE DIRECTION i.e. − π/2 ≤ y ≤ 0.
3. Properties of Inverse Circular Functions:
P−1 (i) sin (sin−1 x) = x, −1 ≤ x ≤ 1
(ii) cos (cos−1 x) = x , −1 ≤ x ≤ 1
(iii) tan (tan−1 x) = x, x ∈ R
(iv) sin−1 (sin x) = x, 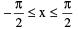
(v) cos−1 (cos x) = x ; 0 ≤ x ≤ π
(vi) tan−1 (tan x) = x ; 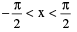
P−2 (i) cosec−1 x = sin−1(1/x) ; x ≤ −1 , x ≥ 1
(ii) sec−1 x = cos−1(1/x) ; x ≤ −1, x ≥ 1
(iii) cot−1 x = tan−1 (1/x) ; x > 0 = π + tan−1(1/x) ; x < 0
P−3 (i) sin−1 (−x) = − sin−1 x , −1 ≤ x ≤ 1
(ii) tan−1 (−x) = − tan−1 x , x ∈ R
(iii) cos−1 (−x) = π − cos−1 x , −1 ≤ x ≤ 1
(iv) cot−1 (−x) = π − cot−1 x, x ∈ R
P−4 (i) sin−1 x + cos−1 x = π/2 −1 ≤ x ≤ 1
(ii) tan−1 x + cot−1 x = π/2 x ∈ R
(iii) cosec−1 x + sec−1 x = π/2 |x| ≥ 1
P−5 tan−1 x + tan−1 y = 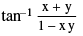 where x > 0, y > 0 & xy < 1
where x > 0, y > 0 & xy < 1
= π + tan−1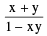 where x > 0, y > 0 & xy > 1
where x > 0, y > 0 & xy > 1
tan−1 x − tan−1y = 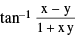 where x > 0, y > 0
where x > 0, y > 0
P−6 (i) sin−1 x + sin−1 y = sin−1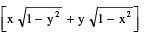 where x ≥ 0, y ≥ 0 & (x2 + y2) ≤ 1
where x ≥ 0, y ≥ 0 & (x2 + y2) ≤ 1
Note that : x2 + y2 ≤ 1 ⇒ 0 ≤ sin−1 x + sin−1 y ≤ π/2
(ii) sin−1 x + sin−1 y = π − sin−1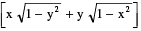 where x ≥ 0, y ≥ 0 & x2 + y2 > 1
where x ≥ 0, y ≥ 0 & x2 + y2 > 1
Note that : x2 + y2 > 1 ⇒ π/2 < sin−1 x + sin−1 y < π
(iii) sin–1x – sin–1y = sin–1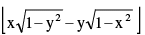 where x > 0 , y > 0
where x > 0 , y > 0
(iv) cos−1 x ± cos−1 y = cos−1 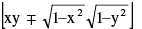 where x ≥ 0 , y ≥ 0
where x ≥ 0 , y ≥ 0
P−7 If tan−1 x + tan−1 y + tan−1 z = tan−1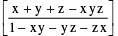 if, x > 0, y > 0, z > 0 & xy + yz + zx < 1
if, x > 0, y > 0, z > 0 & xy + yz + zx < 1
Note : (i) If tan−1 x + tan−1 y + tan−1 z = π then x + y + z = xyz
(ii) If tan−1 x + tan−1 y + tan−1 z = π/2 then xy + yz + zx = 1
P−8 2 tan−1 x = sin−1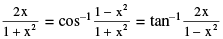 Note very carefully that :
Note very carefully that :
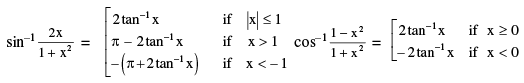
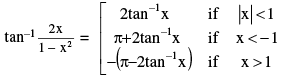
REMEMBER THAT : (i) sin−1 x + sin−1 y + sin−1 z = 3π/2 ⇒ x = y = z = 1
(ii) cos−1 x + cos−1 y + cos−1 z = 3π ⇒ x = y = z = −1
(iii) tan−1 1 + tan−1 2 + tan−1 3 = π and tan−1 1 + tan−1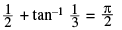
Inverse Trigonometric Functions:
SOME USEFUL GRAPHS
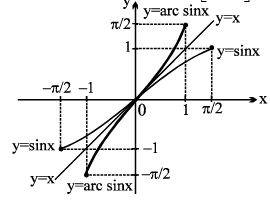
1. y = sin−1 x , |x| ≤ 1, y ∈ 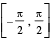
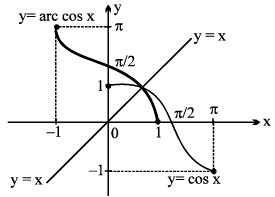
2. y = cos−1 x, |x| ≤ 1 , y ∈ [0, π]
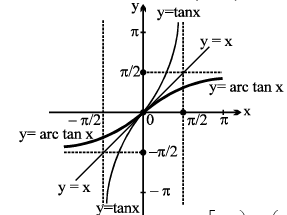
3. y = tan−1 x , x ∈ R,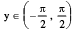
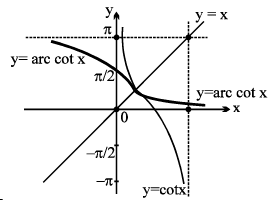
4. y = cot−1 x, x ∈ R , y ∈ (0 , π)
5. y = sec−1 x , |x| ≥ 1 , y 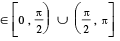
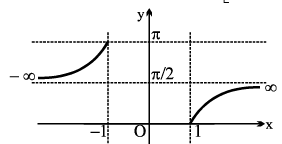
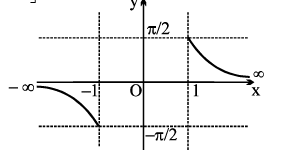
6. y = cosec−1 x , |x| ≥ 1,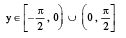
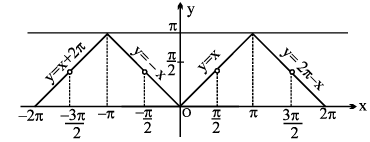
7. (a) y = sin−1 (sin x) , x ∈ R ,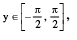
Periodic with period 2 π
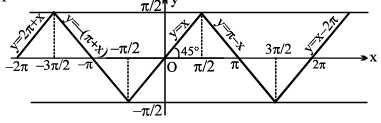
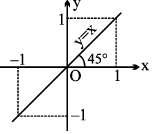
(b) y = sin (sin−1 x), = x x ∈ [−1, 1], y ∈ [−1, 1], y is aperiodic
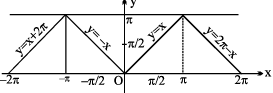
8. (a) y = cos−1(cos x), x ∈ R, y ∈[0, π], = x periodic with period 2 π
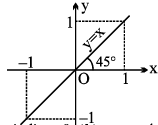
(b) y = cos (cos−1 x), = x
x ∈ [− 1, 1], y ∈ [−1, 1], y is aperiodic
9. (a) y = tan (tan−1 x), x ∈ R, y ∈ R, y is aperiodic = x
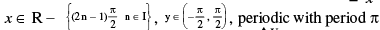
(b) y = tan−1 (tan x), = x
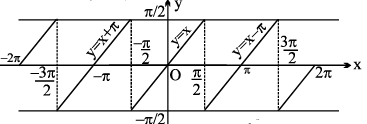
10. (a) y = cot−1 (cot x), = x
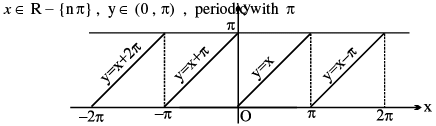
(b) y = cot (cot −1 x), = x
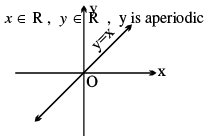
11. (a) y = cosec −1 (cosec x), = x
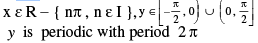
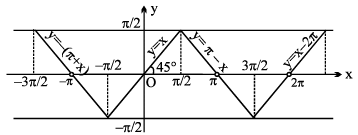
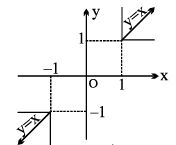
(b) y = cosec (cosec−1 x), = x
|x| ≥ 1 , |y| ≥ 1, y is aperiodic
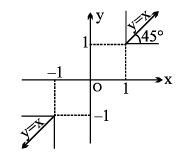
12. (a) y = sec −1 (sec x), = x
y is periodic with period 2π ;
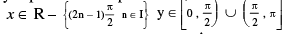
(b) y = sec (sec−1 x), = x
|x| ≥ 1 ; |y| ≥ 1], y is aperiodic
|
203 videos|307 docs|139 tests
|
FAQs on Important Inverse Trigonometric Functions Formulas for JEE and NEET
| 1. What are the principal values and domains of inverse circular functions? |  |
| 2. What are the properties of inverse circular functions? |  |
| 3. What are some important formulas for inverse trigonometric functions in JEE exams? |  |
| 4. How can inverse trigonometric functions be used to solve trigonometric equations? |  |
| 5. What are some frequently asked questions related to inverse trigonometric functions in exams? |  |
















