Important Limit and Continuity & Differentiability of Function Formulas for JEE and NEET

Things To Remember :

1. Limit of a function f(x) is said to exist as, x→a when 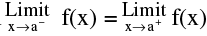= finite quantity.
2. Fundamental Theorems On Limits:
Let 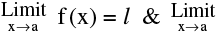g (x) = m. If l & m exists then :
(i)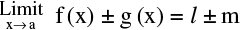 
(ii)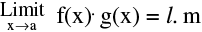 
(iii)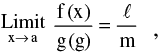provided m ≠ 0
(iv)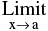kf(x) = k 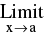f(x)  ; where k is a constant.
(v)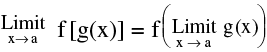= f (m) ; provided f is continuous at g (x) = m.
For example

3. Standard Limits :
(a) 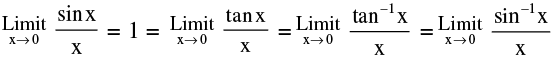 [ Where x is measured in radians ]
(b) 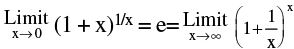note however the re(1 - h )ⁿ = 0and

(c) If 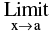f(x) = 1  and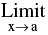Ф (x) = ∞ , then ;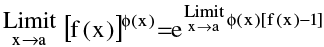
(d) If 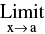f(x) = A > 0 & 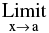Ф (x) = B (a finite quantity) then  ;
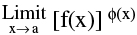= e^z where z = 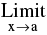Ф (x). ln[f(x)] =  e^BlnA = A^B
(e) 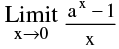= 1n a (a > 0). In particular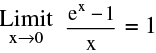
(f)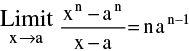

4. Squeeze Play Theorem :
If f(x) ≤ g(x) ≤ h(x) ∀ x  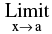& f(x) = l =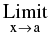h(x)  then  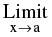g(x) = l.

5. Indeterminant Forms  :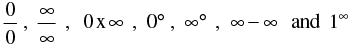

Note :
(i) We cannot plot ∞ on the paper. Infinity (∞) is a symbol & not a number. It does not obey the laws of elementry algebra.
(ii) ∞ + ∞ = ∞
(iii) ∞ × ∞ = ∞
(iv) (a/∞) = 0 if a is finite
(v) a/0 is not defined, if a ≠ 0.
(vi) ab = 0 , if & only if a = 0 or b = 0  and  a & b are finite.

6. The following strategies should be born in mind for evaluating the limits:
(a) Factorisation
(b) Rationalisation or double rationalisation
(c) Use of trigonometric transformation  ; appropriate substitution and using standard limits
(d) Expansion of function like Binomial expansion, exponential & logarithmic expansion, expansion of sinx , cosx , tanx should be remembered by heart & are given below :
(i)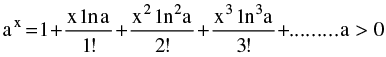
(ii)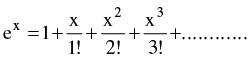
(iii)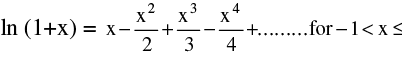
(iv)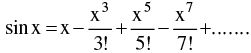
(v)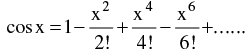 
(vi) 
(vii)
(viii)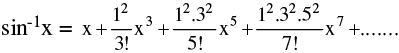
(ix)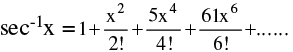 

Clear all your JEE doubts with EduRev Join for Free

Join for Free

(Continuity)

Things To Remember :

1. A function f(x) is said to be continuous at x = c, if 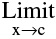f(x) = f(c). Symbolically f is continuous at x = c if 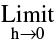f(c - h) =f(c+h) = f(c).
i.e. LHL at x = c = RHL at x = c equals Value of ‘f’ at x = c.
It should be noted that continuity of a function at x = a is meaningful only if the function is defined in the immediate neighbourhood of x = a, not necessarily at x = a.
2. Reasons of discontinuity:
(i) 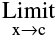 f(x) does not exist
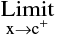i.e. f(x) ≠f (x)
(ii) f(x) is not defined at x= c
(iii) 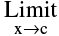 f(x) ≠ f (c)

Geometrically, the graph of the function  will exhibit a break at x= c.

The graph as shown is discontinuous at x = 1 , 2 and 3.

3. Types of Discontinuities :
Type - 1: ( Removable type of discontinuities)
In case 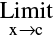f(x) exists but is not equal to f(c) then the function is said to have a removable discontinuity or discontinuity of the first kind. In this case we can redefine the function such that 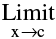f(x) = f(c) & make it continuous at x= c. Removable type of discontinuity can be further classified as :
(a) Missing Point Discontinuity : Where 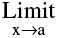 f(x) exists finitely but f(a) is not defined.
e.g. f(x) = 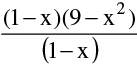has a missing point discontinuity at x = 1 , and f(x) =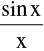

has a missing point discontinuity at x = 0
(b) Isolated Point Discontinuity : Where 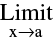f(x) exists & f(a) also exists but ; 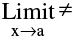f(a). e.g. f(x)  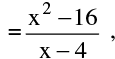x ≠ 4 & f (4) = 9 has an isolated point discontinuity at x = 4.
Similarly f(x) = [x] + [ –x] = 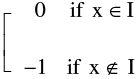has an isolated point discontinuity at all x ∈ I.
Type-2: (Non - Removable type of discontinuities)
In case 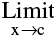f(x) does not exist then it is not possible to make the function continuous by redefining it.
Such discontinuities are known as non - removable discontinuity or discontinuity of the 2nd kind. Non-removable type of discontinuity can be further classified as :
(a) Finite discontinuity  e.g. f(x) = x − [x] at all integral x ; f(x) = tan ⁻¹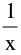at x = 0 and  f(x) = 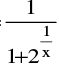at x = 0 (note that f(0⁺) = 0 ; f(0^–) = 1)
(b) Infinite discontinuity e.g. f(x) = 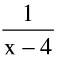or g(x) = 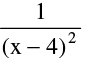at x = 4 ; f(x) = 2^tanx at x = 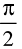and f(x) =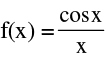at x = 0.
(c) Oscillatory discontinuity e.g. f(x) = sin 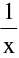at x = 0.
In all these cases the value of f(a) of the function at x= a (point of discontinuity) may or may not exist but 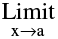does not exist.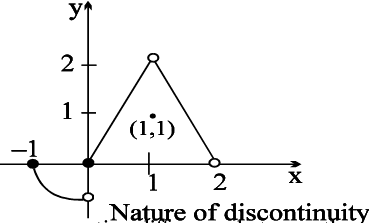

Note: From the adjacent graph note that
–  f is continuous at x = – 1
–  f has isolated discontinuity at x = 1
–  f has missing point discontinuity at x = 2
–  f has non removable (finite type)
discontinuity at the origin.
4. In case of dis-continuity of the second kind the non-negative difference between the value of the RHL at x = c & LHL at x = c is called The Jump Of Discontinuity. A function having a finite number of jumps in a given interval I is called a Piece Wise Continuous Or Sectionally Continuous function in this interval.
5. All Polynomials, Trigonometrical functions, exponential & Logarithmic functions are continuous in their domains.
6. If f & g are two functions that are continuous at x= c then the functions defined by :
F₁(x) = f(x) ± g(x)  ;  F₂(x) = K f(x) , K any real number  ; F₃(x) = f(x).g(x)  are also continuous at x= c.
Further, if g (c) is not zero, thenF₄(x) = 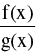is also continuous atx= c.
7. The intermediate value theorem:
Suppose f(x) is continuous on an interval I , and a and b are any two points of I. Then if y₀ is a number between f(a) and f(b) , their exists a number c between a and b such that f(c) = y₀ .
Note Very Carefully That :
(a) If f(x) is continuous & g(x) is discontinuous
at x = a then the product function φ(x) = f(x). g(x)
 is not necessarily be discontinuous at x = a. e.g. f(x) = x & g(x) =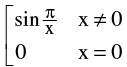

(b) If f(x) and g(x) both are discontinuous at x = a then the product function  φ(x) = f(x). g(x) is not necessarily be discontinuous at x = a. e.g. f(x) = − g(x) =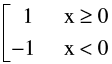

(c) Point functions are to be treated as discontinuous. eg. f(x) = 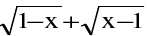is not continuous at x = 1.

(d) A Continuous function whose domain is closed must have a range also in closed interval.
(e) If f is continuous at x = c & g is continuous at x = f(c) then the composite g[f(x)] is continuous at x = c. eg. 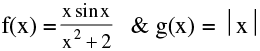are continuous at x = 0 , hence the composite (gof) (x) = 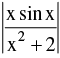will also be continuous at x = 0 .
7. Continuity In An Interval :
(a) A function f is said to be continuous in (a , b) if f is continuous at each & every point ∈(a,b).
(b) A function f is said to be continuous in a closed interval [a , b] if :
(i) f is continuous in the open interval (a , b) &
(ii) f is right continuous at ‘a’ i.e.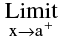f(x) = f(a) = a finite quantity.
(iii) f is left continuous at ‘b’ i.e.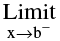f(x) = f(b) = a finite quantity.
Note that a function f which is continuous in [a , b] possesses the following properties :
(i) If f(a) & f(b) possess opposite signs, then there exists at least one solution of the equation f(x) = 0 in the open interval (a , b).
(ii) If K is any real number between f(a) & f(b), then there exists at least one solution of the equation f(x) = K in the open inetrval (a , b).

8. Single Point Continuity:
Functions which are continuous only at one point are said to exhibit single point continuity
e.g. f(x) = 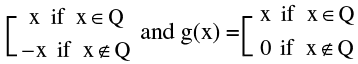are both continuous only at x = 0.

Download the notes Important Formulas: Limit and Continuity & Differentiability of Function

Download as PDF

Download as PDF

Differentiability

Take a Practice Test Test yourself on topics from JEE exam

Practice Now

Practice Now

Things To Remember :

1. Right hand & Left hand Derivatives ; By definition: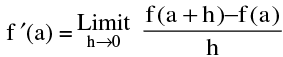
if it exist
(i) The right hand derivative of f ′ at x = a denoted by f ′(a⁺) is defined by :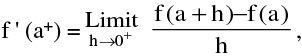

provided the limit exists & is finite.
(ii) The left hand derivative : of f at x = a  denoted by
f ′(a⁺) is defined by : f ' (a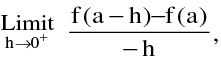^–) = Provided the limit exists & is finite.
We also write f ′(a+) = f ′+(a)  &  f ′(a–) = f ′_(a).
* This geomtrically means that a unique tangent with finite slope can be drawn at x = a as shown in the figure.
(iii) Derivability & Continuity :
(a) If f ′(a) exists then f(x) is derivable at x= a ⇒ f(x) is continuous at x = a.
(b) If a function f is derivable at x then f is continuous at x.
For : f ′(x) = 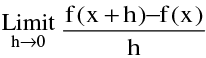exists.
Also f(x + h)-f(x)= 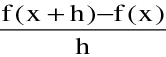h[h ≠ 0]
Therefore : [f (x + h )− f (x)] 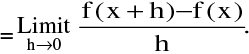h = f '( x ).0 = 0
Therefore 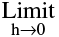[f ( x + h )− f (x )] = 0 ⇒  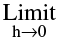 f (x+h) = f(x) ⇒ f is continuous at x.
Note : If f(x) is derivable for every point of its domain of definition, then it is continuous in that domain.

The Converse of the above result is not true:
“ IF f IS CONTINUOUS AT x , THEN f IS DERIVABLE AT x ” IS NOT TRUE.
e.g. the functions f(x) =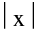 & g(x) = x sin 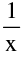; x ≠ 0 & g(0) = 0 are continuous at x = 0 but not derivable at x = 0.
Note Carefully :

(a) Let f ′₊(a) = p & f ′_(a) = q where p & q are finite then :
(i) p = q ⇒ f is derivable at x = a  ⇒ f is continuous at x = a.
(ii) p ≠ q ⇒ f is not derivable at x = a.

It is very important to note that f may be still continuous at x = a.

In short, for a function f :
Differentiability ⇒ Continuity ; Continuity ⇏ derivability ;
Non derivibality ⇏ discontinuous ; But discontinuity ⇒ Non derivability
(b) If a function f is not differentiable but is continuous at x = a it geometrically implies a sharp corner at x = a.
3. Derivability Over An Interval :
f (x) is said to be derivable over an interval if it is derivable at each & every point of the interval f(x) is said to be derivable over the closed interval [a, b] if  :
(i) for the points a and b, f ′(a+) & f ′(b −) exist &
(ii) for any point c such that a < c < b, f ′(c+) & f′(c −) exist & are equal.
Note:

1. If f(x) & g(x) are derivable at x = a then the functions f(x) + g(x), f(x) - g(x) , f(x).g(x) will also be derivable at x = a & if g (a) ≠ 0 then the function f(x)/g(x) will also be derivable at x = a.

2. If f(x) is differentiable at x = a & g(x) is not differentiable at x = a , then the product function F(x) = f(x) g(x) can still be differentiable at x = a e.g. f(x) = x & g(x) = I x |.

3. If f(x) & g(x) both are not differentiable at x = a then the product function ;

F(x) = f(x)- g(x) can still be differentiable at x = a e.g. f(x) = | x | & g(x) = I x |.

4. If f(x) & g(x) both are non-deri. at x = a then the sum function F(x) = f(x) + g(x) may be a differentiable function. e.g. f(x) = | x | & g(x) = -| x |.

5. If f(x) is derivable at x = a ⇏ f '(x) is continuous at x = a.

6. A surprising result : Suppose that the function f (x) and g (x) defined in the interval (x₁, x₂) containing the point x₀, and if f is differentiable at x = x₀ with f (x₀) = 0 together with g is continuous as x = x₀ then the function F (x) = f (x) · g (x) is differentiable at x = x₀ e.g. F (x) = sinx · x^2/3 is differentiable at x = 0.