Important Questions: Perimeter and Area | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Q1: A rectangular piece of land has a length of 500 m and a breadth of 300 m respectively. Find the area and the cost of the land. The condition given is 1 m2 of the land cost Rs 10,000.
Ans: According to the given question,
The length of the rectangular land = 500 m
The breadth of the rectangular land = 300 m
Since the formula for area = length × breadth = 500 × 300 m2 = 150000 m2
If Rs 10,000 is the cost of land of 1m2
Then the cost of 150000 m2 land = 10,000 × 150,000 = Rs 1,500,000,000
Q2: The perimeter is given at 320 m. Calculate the area of the square park.
Ans: According to the given question,
The perimeter of the square = 320 m
Length of the side of the park = 320/4 = 80 m
Since 4 × length of the side of the park = 320 m
Area of the square park = (length of the park side)² = (80)² = 6400 m²
Q3: Calculate the breadth and perimeter of the rectangular plot when the area given is 440 m2 and the length given is 22 m.
Ans:
According to the given question,
The Area of the given rectangular plot = 440 m2
Length of the plot = 22 m
Applying the formula, area = length × breadth
Therefore, area/length = breadth
Breadth = 440/22 = 20 m
Perimeter of the rectangle will be calculated as = 2(length + Breadth) = 2(22 + 20) = 2 × 42 = 84 m.
The rectangular plot has a breadth of 20 m and a perimeter of 84 m.
Q4: Calculate the breadth when the perimeter and length of the rectangular sheet given are 100 cm and 35 cm respectively. Also, calculate the area.
Ans: According to the given question,
The perimeter given is 100 m
The length of the rectangular sheet given is 35 cm
Since perimeter = 2 ( length + breadth )
On applying the formula
100 = 2 × (35 + b)
100/2 = 35 + b
50 = 35 + b
50 – 35 = b
b = 15 cm
Therefore, the breadth is calculated as 15 cm.
Since we know that the
Area = length × breadth = 35 × 15 = 525 cm2
Therefore, the area of the rectangular sheet is 525 cm².
Q5: The square park and the rectangular park have the same area. Calculate the breadth of the rectangular park when the side of the rectangular park is 60 m and the length of the rectangular park is 90 m.
Ans:
According to the given question,
the Area of the square park = area of the rectangular park
Area of the square park:
Side of the square = 60 m
Area = (side)2 = (60 m)2 = 3600 m2
Since both parks have the same area, the area of the rectangular park is also 3600 m2. Using the formula for the area of a rectangle:
Area of the rectangular park:
Area = length × breadth
3600 m2 = 90 m × breadth
Breadth = 3600 / 90 = 40 m
Thus, the breadth of the rectangular park is 40 m.
Q6: Suppose the shape of the wire is a rectangle. The length and breadth of the rectangle are 40 cm and 22 cm respectively. What is going to be the measurements of each side if the wire is bent in the shape of a square? Find out about the shape which encloses more area.
Ans: The perimeter of the square is equal to the perimeter of the rectangle since the wire shape is altered but its total length remains unchanged.
Given:
- Length of the rectangle = 40 cm
- Breadth of the rectangle = 22 cm
Since the perimeters are equal, we can equate them as follows:
2 × (length + breadth) = 4 × side of square
Substituting the given values:
2 × (40 + 22) = 4 × side of square
2 × 62 = 4 × side of square
124 = 4 × side of square
Side of square = 124 / 4 = 31 cm
Next, let us calculate the areas:
Area of the rectangle = length × breadth = 40 × 22 = 880 cm2
Area of the square = side2 = 31 × 31 = 961 cm2
Comparing the two areas, it is clear that the square encloses more area than the rectangle.
Q7: The length of the door is 2 m and the breadth is 1 m and it is fitted in a wall. The wall has a length of 4.5 m and a breadth of 3.6 m, what is the cost required for whitewashing the wall when the rate is Rs 20 per m2 for whitewashing?
Ans: To determine the cost of whitewashing the wall, we first calculate the areas involved.
Door dimensions: Length = 2 m, Breadth = 1 m
Area of the door = Length × Breadth = 2 × 1 = 2 m2
Wall dimensions: Length = 4.5 m, Breadth = 3.6 m
Area of the wall = Length × Breadth = 4.5 × 3.6 = 16.2 m2
The area to be whitewashed is the total wall area minus the door area: 16.2 m2 - 2 m2 = 14.2 m2.
Given the rate of whitewashing is Rs 20 per m2, the total cost is: 14.2 × 20 = Rs 284.
Thus, the cost required for whitewashing the wall is Rs 284.
Q8: PQRS is a parallelogram, QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm then calculate the area of the parallelogram PQRS. Calculate QN when PS gave as 8 cm.
Ans:
SR = 12 cm, QM = 7.6 cm
Area of the parallelogram = length × breadth = SR × QM = 12 × 7.6 = 91.2 cm2
For the second part of the question, calculating QN includes:
Area of the parallelogram = length × breadth
91.2 = PS × QN
91.2 = 8 × QN
QN = 91.2/8 = 11.4 cm
Q9: DL and BM are the heights on sides AB and AD respectively of ABCE parallelogram. Let us suppose the area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm. Calculate the length of the BM and the DL.
Ans: According to the question given above,
The Area of the parallelogram = 1470 cm2
AB = 35 cm
AD = 49 cm
Then
It is clear that
The Area of the parallelogram = base × height
1470 = AB × BM
1470 = 35 × DL
1470/35 = DL
DL = 42 cm
Area of the parallelogram = base × height
1470 = AD × BM
1470 = 49 × BM
BM = 1470/49
BM = 30 cm
Q10: The right-angled triangle is ABC given. This is right-angled at A. AD is perpendicular to BC. If AB = 5 cm and BC = 13 cm and AC = 12 cm. Calculate the area of the ABC. Also, calculate the length of the AD.
Ans: According to the given question,
AB = 5 cm
BC = 13 cm
AC = 12 cm
We know that
Area of the triangle ABC = ½ × Base × height
= ½ × AB × AC
=½ × 5 × 12 = 1 × 5 × 6 = 30 cm2
Now,
Area of the triangle ABC = ½ × Base × height
30 = ½ × AD × BC
30 = ½ × AD × 13
30 × 2/13 = AD
AD = 60/13 = 4.6 cm
Q11: Find the circumference of the circle with a radius of 14 cm. take the value of π =22/7.
Ans:
Given, the radius of the circle = 14 cm
Circumference of the circle will be calculated by the formula = 2 π r
= 2 × 22/7 ×14
= 2 × 22 × 2
= 88 cm
Q12: The circumference of a circular sheet is 154 m. calculate the radius. Calculate the area of the sheet as well.
Ans:
As per the question, it is given that
The Circumference of the circle = 154 m
We know the formula
Circumference of the circle will be calculated by the formula = 2 r
154 = 2 × 22/7 × r
154 = 44/7 × r
r = 154 × 7/ 44
r = 14 × 7/ 4
r = 7 × 7/ 2
r = 49/2 = 24.5 m
Area of the circle = π r2 = 22/7 × (24.5)2 = 22/7 × 600.25
= 22 × 85.75 = 1886.5 m2
Q13: Calculate the perimetre of the figure. The figure is a semicircle including its diameter.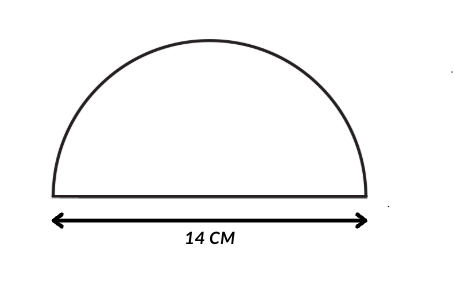
Ans: As per the given question,
The Diameter of the semi-circle = 14 cm
Radius = r = d/2 = 14/2 = 7 cm
Circumference of the semi-circle = 22/7 × 7 = 22 cm
To calculate the perimeter of the above figure,
Perimeter of the semi-circle = semi-circle circumference + semicircle diameter
= 22 + 14 = 36 cm
Q14: The rate of polishing is Rs 15/m2. Find the cost of polishing a circular table – top which has a diameter of 1.6 m.
Ans: As per the given question,
The diameter of the circular table – top = 1.6 m
As we know the
Radius = r = d/2 = 1.6 / 2 = 0.8 m
Area of the circular table top will be 3.14 × 0.8 × 0.8 = 2.0096 m2
The cost of polishing 1 m2 area = Rs 15
So for calculating the 2.0096 m2 area = Rs 15 × 2.0096 = 30.144
So in order to polish the area of 2.0096 m2, the cost incurred is Rs 30.144
Q15: Fill in the blanks:
- ________ is the distance around a closed figure.
- _________ is the part of the plane which is occupied by the closed figure.
- The formula to calculate the perimetre of the square will be presented as _______
- The formula to calculate the perimetre of the rectangle will be presented as _______
- The area of the square is calculated as ________
- The area of a rectangle is calculated as ________
- The area of the parallelogram is calculated as _______
- ___________ is the distance around a circular region.
Ans:
- Perimeter is the distance around a closed figure.
- Area is the part of the plane which is occupied by the closed figure.
- The formula to calculate the perimetre of the square will be presented as 4 × side
- The formula to calculate the perimetre of the rectangle will be presented as 2 × (length + breadth)
- The area of the square is calculated as side × side
- The area of a rectangle is calculated as length × breadth
- The area of the parallelogram is calculated as base × height
- Circumference is the distance around a circular region.
|
77 videos|386 docs|39 tests
|
FAQs on Important Questions: Perimeter and Area - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What is the formula for calculating the perimeter of a rectangle? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What are the units used to measure perimeter and area? |  |
| 4. How can I calculate the area of a circle? |  |
| 5. What is the difference between perimeter and area? |  |
















