Important Definitions & Formulas: Real Numbers | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Important Definitions |

|
| 1. Real Numbers |

|
| 2. Fundamental Theorem of Arithmetic |

|
| 3. Rational Numbers |

|
| 4. Irrational Number |

|
| 5. Prime Number |

|
| Important Formulas with Examples |

|
The chapter on "Real Numbers" is crucial for understanding the properties and relationships of numbers, forming the basis for solving a wide range of mathematical problems in various fields.
This document provides Class 10 Maths Formulas for Real Numbers that can help you to succeed in board exams and in future competitive exams.
Important Definitions
1. Real Numbers
- Real numbers constitute the union of all rational and irrational numbers.

- In general, all the arithmetic operations can be performed on these numbers and they can be represented on the number line, also.
2. Fundamental Theorem of Arithmetic
- Every composite number can be factorized as a product of primes and this factorization is unique, apart from the order in which the prime factors occur.
- Example: 54=2×3×3×3
- Therefore, 54 is represented as a product of prime factors (One 2 and three 3s) ignoring the arrangement of the factors.
- Also, the number 120 can be factorized as 2 × 2 × 2 × 3 × 5. The prime factors are 2, 2, 2, 3, and 5. The order of the factors doesn't matter, as the Fundamental Theorem of Arithmetic guarantees a unique factorization regardless of the arrangement of the prime factors.
Example 1: What is the HCF of 36 and 48 using prime factorization?
Solution: To find the HCF using prime factorization, follow these steps:
1. Find the prime factors of each number.
Prime factors of 36: 2 × 2 × 3 × 3 = (22 × 32)
Prime factors of 48: 2 × 2 × 2 × 2 × 3 = (24 × 3)
2. Find the common prime factors.
Common prime factors: 2 × 2 × 3 = (22 × 3)
3. Multiply the common prime factors to get the HCF.
HCF = 2 × 2 × 3 = 12
So, the HCF of 36 and 48 using prime factorization is 12.
Example 2 : Consider the number 4n, where n is a natural number. Is there any value of n for which 4n ends with the digit zero? Justify your answer.
Solution:If 4n, for any n, were to end with the digit zero, it would need to be divisible by 10. For a number to be divisible by 10, its prime factorization must include both the primes 2 and 5.The prime factorization of 4n is:
4n=(2)2n
This shows that the only prime factor in 4n is 2. Since there is no 5 in the factorization, 4n cannot be divisible by 10.
Thus, by the Fundamental Theorem of Arithmetic, which ensures the uniqueness of prime factorization, there are no natural numbers n for which 4n ends with the digit zero.
3. Rational Numbers
The decimal expansion of every rational number is either terminating or non-terminating repeating.
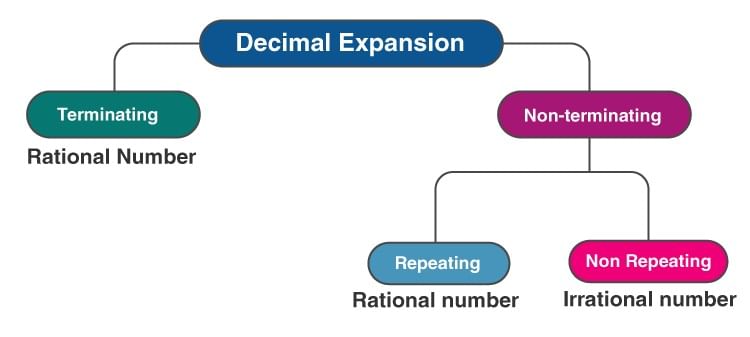
- Terminating Decimal Representation: Let x be a rational number with a terminating decimal representation. Then we can express x as p/q where p and q are coprime, and the prime factorization of q is of the form 2n 5m, where n, m are some non-negative integers.
- Non-terminating Decimal Representation: The rational number p/q will have a non-terminating repeating(recurring) decimal representation if, in standard form, the prime factorization of q is not of form 2n 5m, where n, m is some non-negative integers.
4. Irrational Number
- A number is irrational if and only if, its decimal representation is non-terminating and non-repeating (non-recurring).
OR

- A number that cannot be expressed in the form of p/q, q ≠ 0 and p, q ∈ I, will be an irrational number. The set of irrational numbers is generally denoted by S.
Example 3: Prove that 3 + 2√5 is irrational.
Solution: Let 3 + 2√5 be a rational number.
Then the co-primes x and y of the given rational number where (y ≠ 0) is such that:
3 + 2√5 = x/y
Rearranging, we get,
2√5 = (x/y) – 3
√5 = 1/2[(x/y) – 3]
Since x and y are integers, thus, 1/2[(x/y) – 3] is a rational number.
Therefore, √5 is also a rational number. But this confronts the fact that √5 is irrational.
Thus, our assumption that 3 + 2√5 is a rational number is wrong.
Hence, 3 + 2√5 is irrational.
5. Prime Number
A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and the number itself.
In other words, a prime number cannot be formed by multiplying two smaller natural numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, and so on.
Example 4: Express each number as a product of its prime factors:
(i) 140
(ii) 156
Solution: (i) 140
Using the division of a number by prime numbers method, we can get the product of prime factors of 140.
Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 22 × 5 × 7(ii) 156
Using the division of a number by prime numbers method, we can get the product of prime factors of 156.Hence, 156 = 2 × 2 × 13 × 3 = 22 × 13 × 3
Important Formulas with Examples
LCM & HCF of Two Numbers
For any two positive integers p and q, we have:
HCF (p, q) x LCM [p, q] = p x q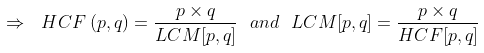

Example 5: Given that HCF (306, 657) = 9, find LCM (306, 657).
Solution: As we know that,
HCF × LCM = Product of the two given numbers
So, 9 × LCM = 306 × 657
LCM = (306 × 657)/9
LCM = 22,338
Therefore, LCM (306,657) = 22,338
|
127 videos|584 docs|79 tests
|
FAQs on Important Definitions & Formulas: Real Numbers - Mathematics (Maths) Class 10
| 1. What are real numbers and how are they classified? |  |
| 2. What is the Fundamental Theorem of Arithmetic? |  |
| 3. How do you define rational numbers, and can you provide examples? |  |
| 4. What are irrational numbers, and can you give some examples? |  |
| 5. How can we identify prime numbers, and what are some examples? |  |





















