Indeterminate Forms | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| What is Indeterminate Form? |

|
| Indeterminate Forms List |

|
| How to Evaluate Indeterminate Forms? |

|
| Solved Numericals |

|
What is Indeterminate Form?
In mathematics, there are certain expressions for which it is impossible to determine a definitive value. Such expressions are referred to as indeterminate forms. Indeterminate forms often arise when evaluating the limits of functions, particularly when the limit involves the ratio of two functions that both approach zero.Indeterminate Forms of Limits
Some forms of limits are called indeterminate if the limiting behaviour of individual parts of the given expression is not able to determine the overall limit.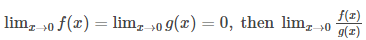
If the limits are applied for the given function, then it becomes 0/0, which is known as indeterminate forms.
In Mathematics, there are seven indeterminate forms that include 0, 1 and ∞, They are
0/0, 0×∞,∞/∞, ∞ −∞, ∞0, 00, 1∞.
Indeterminate Forms List
Some of the indeterminate forms with conditions and transformation are given below:
Indeterminate Form 1
0/0
Indeterminate Form 2
∞/∞
Indeterminate Form 3
0 x ∞
Indeterminate Form 4

Indeterminate Form 5
00
Indeterminate Form 6
∞0
Indeterminate Form 7
∞ – ∞
How to Evaluate Indeterminate Forms?
There are three methods used to evaluate indeterminate forms. They are:- Factoring Method (0/0 form): In the factoring method, the expressions are factored to their maximum simplest form. After that, the limit value should be substituted.
- L’Hospital’s Rule (0/0 or ∞/∞ form): In this method, the derivative of each term is taken in each step successively until at least one of the terms becomes free of the variable. It means that at least one term becomes constant.
- Division of Each Term by Highest Power of Variable (∞/∞ form): In this method, each term in numerator and denominator is divided by the variable of the highest power in the expression, and then, the limit value is obtained.
Solved Numericals
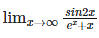
Solution: 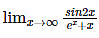
Let f(x) = sin 2(x) and g(x) = ex. + x
Therefore, f’(x) = 2 cos 2x , g’(x) = ex + 1
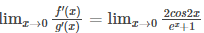
Now, substitute the limits, it becomes
= 2 cos(0)/ e0 + 1
= 2/ 2 = 1
Therefore 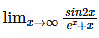 = 1
= 1
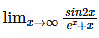 = 1
= 1
The document Indeterminate Forms | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) is a part of the Electrical Engineering (EE) Course Engineering Mathematics for Electrical Engineering.
All you need of Electrical Engineering (EE) at this link: Electrical Engineering (EE)
|
44 videos|109 docs|58 tests
|
FAQs on Indeterminate Forms - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are some examples of indeterminate forms? |  |
Ans. Some examples of indeterminate forms include 0/0, ∞/∞, 0*∞, ∞ - ∞, and 0^0.
| 2. How can indeterminate forms be evaluated? |  |
Ans. Indeterminate forms can be evaluated using techniques such as L'Hôpital's Rule, factoring, common denominator, or substitution to simplify the expression and determine the limit.
| 3. Can all indeterminate forms be resolved using L'Hôpital's Rule? |  |
Ans. No, not all indeterminate forms can be resolved using L'Hôpital's Rule. Some forms may require other techniques such as factoring or substitution to find the limit.
| 4. Why are indeterminate forms important in mechanical engineering? |  |
Ans. Indeterminate forms play a crucial role in mechanical engineering as they often arise in the analysis of structures, forces, and vibrations, requiring precise mathematical calculations to determine solutions.
| 5. How can understanding indeterminate forms benefit mechanical engineers? |  |
Ans. Understanding indeterminate forms can help mechanical engineers accurately analyze and design complex systems, optimize performance, and ensure structural stability by solving challenging mathematical problems effectively.
Related Searches




















