Integer Answer Type Questions: Differentiation | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Assertion & Reason Type Question
Q. 1. Let f (x) = 2 + cos x for all real x.
STATEMENT - 1 : For each real t, there exists a point c in [t, t + π] such that f '(c) = 0 because
STATEMENT - 2 : f(t) = f(t + 2π) for each real t.
(a) Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1
(b) Statement-1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
(c) Statement-1 is True, Statement-2 is False
(d) Statement-1 is False, Statement-2 is True.
Ans. (b)
Solution. Given that f (x) = 2 + cos x which is continuous and differentiable every where.
Also f ' (x) = – sin x ⇒ f ' (x) = 0 ⇒ x = nπ
⇒ There exists c ∈ [t, t + p] for t ∈ R
Such that f ' (c) = 0
∴ Statement-1 is true.
Also f (x) being periodic of period 2π, statement-2 is true, but statement-2 is not a correct explanation of statement-1.
Q. 2. Let f and g be real valued functions defined on interval (–1, 1) such that g" (x) is continuous, g (0) ≠ 0. g'(0) = 0, g ''(0) ≠ 0 , and f (x) = g (x) sin x
STATEMENT - 1 : 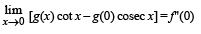 and
and
STATEMENT - 2 : f '(0) = g(0)
(a) Statement - 1 is True, Statement - 2 is True; Statement
- 2 is a correct explanation for Statement - 1
(b) Statement - 1 is True, Statement - 2 is True; Statement
- 2 is NOT a correct explaination for Statement - 1
(c) Statement - 1 is True, Statement - 2 is False
(d) Statement - 1 is False, Statement - 2 is True
Ans. (a)
Solution. We have f (x) = g(x) sin x
⇒ f '(x) = g'(x) sin x + g(x) cos x
⇒ f '(0) = g'(0) × 0 + g(0) = g(0) [∴ g'(0) = 0]
∴ Statement 2 is correct.
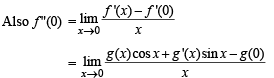
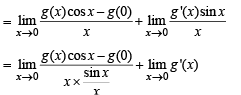
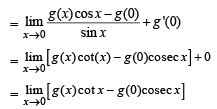
∴ Statement 1 is also true and is a correct explanation for statement 2.
Integer Value Correct Type Question
Q. 1. If the function 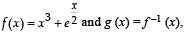 then the value of g' (1) is
then the value of g' (1) is
Ans. 2
Solution. Given that f (x) = x3+e x /2 and g (x) = f -1 (x) then we should have gof ( x) = x
⇒ g(f (x)) = x ⇒ g(x3 +ex/2) = x
Differentiating both sides with respect to x, we get
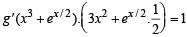
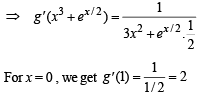
Q. 2. 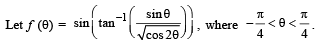
Then the value of 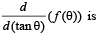
Ans. 1
Solution.
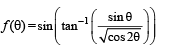
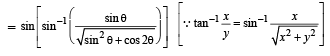
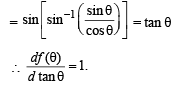
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Differentiation - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is differentiation in calculus? |  |
| 2. How is differentiation useful in real life? |  |
| 3. What are the basic rules of differentiation? |  |
| 4. How can differentiation be used to find maximum and minimum points of a function? |  |
| 5. Can differentiation be used to calculate rates of change in business and economics? |  |





















