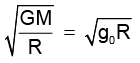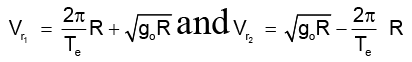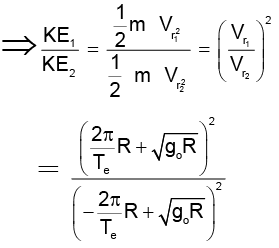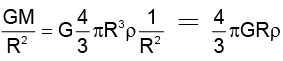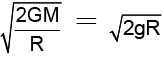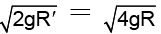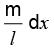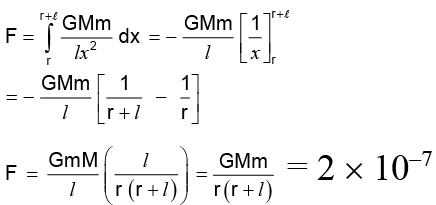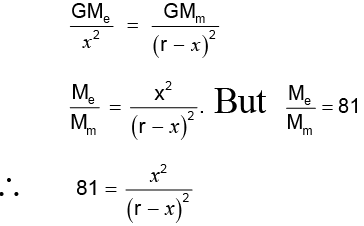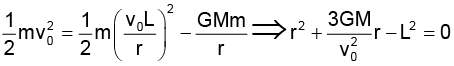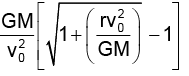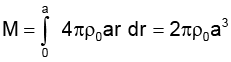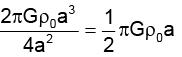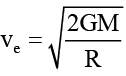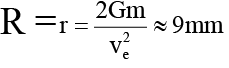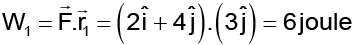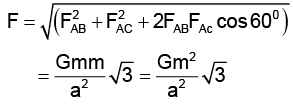Integer Answer Type Questions for JEE: Gravitation | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. Two satellites A and B, of equal mass, move in the equatorial plane of earth close to the earth's surface.  Satellite A moves in the same direction as that of the rotation of the earth while satellite B moves in the opposite direction.  Determine the ratio of the kinetic energy of B to that of A in the reference frame fixed to earth. 

Ans. 1.265
The orbital speed of a satellite very close to earth = V₀ =
The peripheral speed of earth = V_e = Rω_e = 2π/T_e R
⇒ The velocities of the satellites relative to earth are given by

Positive and Negative sign are for the satellites orbiting form east to west and west to east respectively because earth rotates from west to east

Putting R = 6.4 x 10⁶ m, g₀ = 9.8 m/sec² and T_e = 86400 sec,  KE₁/KE₂ = 1.265

Q.2. If the radius and density of a planet are two times and half respectively of those of earth, find the intensity of gravitational field at planet surface and escape velocity from planet.

Ans.  15.84

Acceleration due to gravity g =
Thus = 1 ∴ g₂ = g₁ = g
Escape velocity V_e =
∴ Escape velocity at planet =
= (√2) (11.2km / sec ) = 15.84 km/sec.

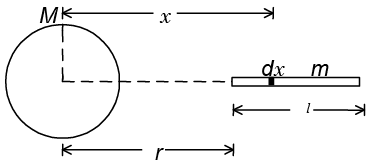
Q.3. A uniform sphere of mass M = 100 kg and a thin uniform rod of length l = 30cm and mass m = 300 kg oriented as shown in the figure. The distance of centre of sphere to the nearest end of the rod is r = 3 m. The gravitation force between them is given as x x 10^–8 N. Find x   (G = 6.6 x 10^–11 Nm²/kg²)

Ans. 20

Since the sphere is uniform its entire mass may be considered to be concentrated at its centre. The force on the elementary mass dm is
dF = GMdm/x²
But dm =

N
x = 20

Q.4. The distance between earth and moon is 4×105 km and the mass of earth is  81 times the mass of moon. Find the position (take 10⁴ km as unit) of a point on the line joining the centres of earth and moon, where the gravitational field is zero.

Ans. 36
Let x be the distance of the point of no net field from earth. The distance of this point from moon is  (r – x), where r = 3.8 x 10⁵ km.  

The gravitational field due to earth = GM_e/x²  and that due to moon = For the net field to be zero these are equal and 

opposite.

x/r-x = 9
9r – 9x = x
10x = 9 r

x = 9/10 r = 9/10 x 4 x 10⁵ = 3.6 × 10⁵ km = 36 x 10⁴ km ⇒ x = 36 unit

Q.5. A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m/s as it reaches A. The work done by the person on the mass is –3J. The potential at infinity is –10 J. Then find the potential at A.

Ans. 5
Work done by external agent
W_ent, = ΔU + ΔK
= U_A – U_∞ + K_A - K_∞
= U_A – 10 + 1/2 x mv² – 0
–3 = U_A – 10 + 1/2 x 1 x 4
+ 5 J = U_A
So V_A = 5 J/kg

Q.6. A cosmic body A moves towards star with velocity v₀ (when far from the star) and aiming parameter L and arm of velocity vector v₀ relative to the centre of the star as shown in figure. Find the minimum distance (take 10⁸ m as unit) by which this body will get to the star. Mass of the star is M.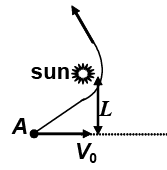

[M = 10²⁰ kg, G = 2/3 x 10^-10 Nm²/kg², v₀ =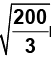m/s, L = √15 x 10⁸ m]

Ans. 3
r =  minimum distance conservation of angular momentum about star mv₀L = mrv₁
;

Solving r =
Putting the values r = 3 x 10⁸ m = 3 unit

Q.7. The density inside an isolated large solid sphere of radius a = 4 km is given by r = ρ₀a/r  where ρ₀ is the density at the surface and equals to 10⁹ kg/m³ and r denotes the distance from the centre. Find the gravitational field (in m/s²) due to this sphere at a distance 2a from its centre. Take G = 6.65 x 10^–11 Nm²/kg².

Ans. 418

The gravitational field at the given point is  E =...(i)
The mass M may be calculated as follows. Consider a concentric shell of radius r and thickness dr. Its volume is  dV = 4πr²) dr
and its mass is = dM = ρdv = (4πr²dr) = 4πρ₀ar dr.
The mass of the whose sphere is
Thus, by (i) the gravitational field is E =
∴ m/s2 ⇒ E = 418 m/s²

Q.8. A mass of 6 × 10²⁴ kg (equal to the mass of the earth) is to be compressed in a sphere in such a way that the escape velocity from its surface is 3 × 10⁸ ms^–1. What should be the radius of the sphere in 'mm'. where G = 6.75 × 10^–11 Nm²/kg².

Ans. 9

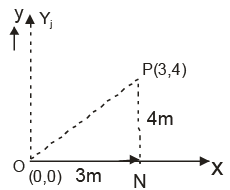
Q.9. The gravitational field in a region is given by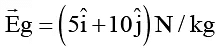. The work done by an external agent in carrying a mass of 0.4 kg from point (0,0) to point (3,4) metre is found y x 11J. Find y.

Ans. 2
Gravitational force on mass 

 Newton

Gravitational field is conservative, so work done by internal energy against gravitational field is independent of path. So work done in displacing the mass from 0 to P directly is same as displacing the mass along path ONP. Work done by gravitational field from displacement from O to N is

Work done by gravitational field from displacement N to P is
= 16 joule
⇒ 22 = (11) y = y = 2.

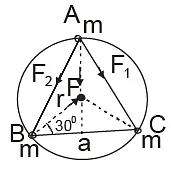
Q.10. Three particles each of mass m, are situated at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original separation a. The initial velocity that what should be given to each particle is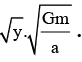Find y.

Ans. 1

Let three particles each of mass m be located at vertices A, B and C of equilateral triangle. These particles move on circular path with centre at O, under their mutual gravitational interactions. The side of triangle = a
r = a/√3
Net force on particle A

This force provides the necessary centripetal force i.e.