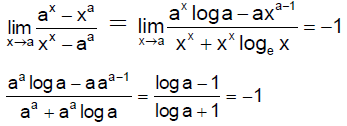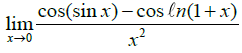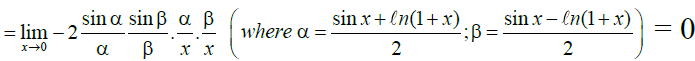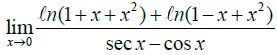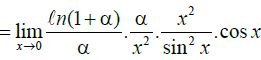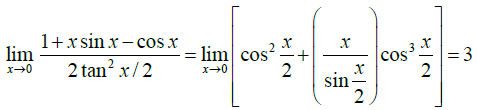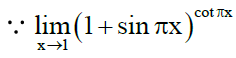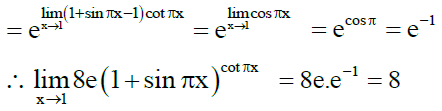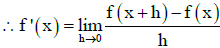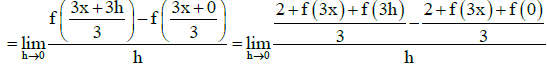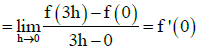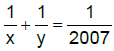Integer Answer Type Questions for JEE: Limits, Continuity & Differentiability | Chapter-wise Tests for JEE Main & Advanced PDF Download

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Q.1. If 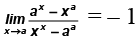 then find the value of a.

Ans. 1
Since, the given limit is in the form of 0/0, we will use L’ Hospital’s Rule

It is satisfied only when a = 1.

Q.2.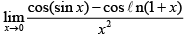

Ans. 0

Q.3.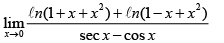  

Ans. 1


where α = x⁴  + x² = 1

Q.4. The value of  is

Ans. 3

Q.5. The value of 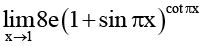 must be 

Ans. 8

Q.6. Let f(x) = [x]+ |1 - x|, -1 ≤ x ≤ 3 and [x] is the largest integer not exceeding x. The number of points in [-1, 3] where f is not continuous is

Ans. 4
f(x) = [x] + |1 - x|,  -1 ≤ x ≤ 3
= -x if -1 ≤ x < 0
=1 - x if 0 ≤ x <1 = x if 1 ≤ x < 2
= x +1 if 2 ≤ x < 3 = 5 if x = 3
Clearly f is not continuous at x = 0, 1, 2 and 3

Q.7. Let f : R → R be a differential function satisfying 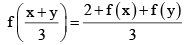 for all real x and y and f'(2) = 2. If g(x) = f(| x |)- 3| for all x ∈ R , then for g(x) total non-differentiable point are 

Ans. 3



⇒ f '(2) = f'(0) = 2 (∵ f'(2) = 2) ⇒ f'(x) = 2 ⇒f(x)= 2x + c
Put x = y = 0 in
Now, from equation (i), f(0) = 0 + c = 2
∴ c = 2
From equation (i), f(x) = 2x + 2
So, function g(x) = |2|x| - 1|, hence the points of non-differentiability of g(x) are
x = ±(1/2), 0

Q.8. Let f(x) = 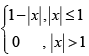g(x) = f (x -1) + f (x + 1). Then the number of points where g is not differentiable is

Ans. 5

⇒ (x + y)2007 = xy ⇒ xy - 2007x - 2007y = 0
(x - 2007)(y - 2007) = 2007² = 3⁴ x 223²
The number of pairs is equal to the number of divisors of 2007² that is (4 + 1) x (2 + 1) = 15
Since, x < y, so required number of pairs = 7

Q.9. Let f (x) = 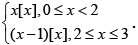 If m is the number of points in [0, 3]where f is discontinuous and n is the number of points in [0, 3]where f is not differentiable, then the value of m + n is

Ans. 5

f is discontinuous at x = 1 and x = 3 only
Also, f'(0) = 0 and f is not derivable at x = 2
So m = 2 and n = 3.

Q.10. Let f(x) = x tan^-1(x²) + x⁴. Let f^k(x) denotes kth derivative of f(x) w.r.t. x, k ∈ N. If f ^2m(0) ≠ 0 m ∈ N then m equals 

Ans. 2
Let g(x) = x tan^-1 (x²). It is an odd function. So, g^2m (0) = 0.
Let h(x) = x⁴.
So, f(x) = g(x) + h(x) ⇒ f^2m (0) = g^2m(0) + h^2m(0) = h^2m (0) ≠ 0.
It happens when 2m = 4 ⇒ m = 2.