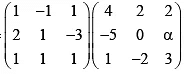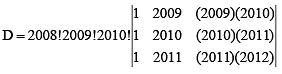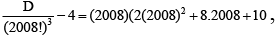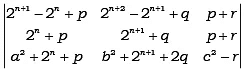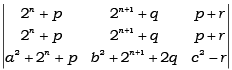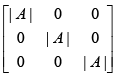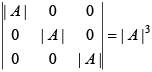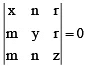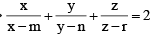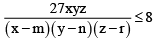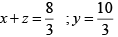Integer Answer Type Questions for JEE: Matrices & Determinants | Chapter-wise Tests for JEE Main & Advanced PDF Download

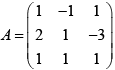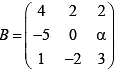Q.1. ; 10  If B =A^-1 then value of α is

Ans. 5
B = A^-1;
AB = I
10I = 10AB =
=
 ∴ α = 5

Q.2. If 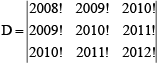 then 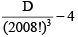 is divisible by 

Ans. 2008

=  
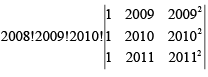
∴ = 2(2009)²(2010)

which is divisible by 2008.

Q.3. If p, q, r are in A.P., then the determinant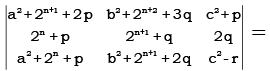  

Ans. 0
Applying R₁ ⇒ R₁- R₃ and 2q = p + r
=
=
= 0

Q.4. For a 3 ´ 3 matrix A, if det A = 4, then det (Adj A) equals

Ans. 16
Since A Adj A = | A | I
=
∴ det (A Adj A)
=
∴  |A| |Adj A| = |A|³
∴ |Adj A| = |A|² = (4)² = 16 

Q.5. If x > m, y > n, z > r (x, y, z > 0) such that 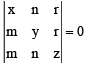 then find the greatest value of .

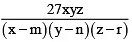Ans. 8

⇒
Now  AM ≥ GM
⇒

Q.6. If the system of equations x + ay = 0, az + y = 0, ax + z= 0 has infinite solutions then  | a|=

Ans. 1
x = -ay;
ax +  z =0 ⇒ -a²y + z = 0
az + y =0 ⇒ a³y+ y =0
∴ a = -1 ; | a |= 1

Q.7. The value of l for which the system of equations 2x - y + 2z = 2, x - 2y + z = -4, x + y + lz = 4 has no solution is

Ans. 1
2x - y + 2z = 2; y = 2(x + z -1)
x - 2y + z = -4 ⇒ x + z + 4 = 4(x + z) - 4
3( x +z )= 8

x + y + λz = 4
x + λz = 2/3
(1 - λ) z = 2
∴ λ = 1

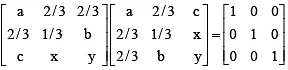
Q.8. Find c² + x² + y² if the matrix A given by 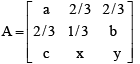 is orthogonal.

Ans. 1
It is given that the matrix A is orthogonal. Therefore,
 
Comparing the element in the 3^rd column of 3^rd row, we get c² + x² + y² = 1.

Q.9. 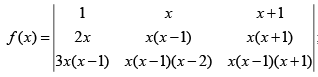; f (100) = ?

Ans. 0
Take x from R₂ ,R₃
x - 1 from R₃
x  + 1 from C₃
 
f (100) = 0

Q.10. The number of value of t for which the system of equations
(a – t)x + by + cz = 0
bx + (c – t)y + az = 0
and cx + ay + (b – t) z = 0 has non trivial solution

Ans. 3
System of equation have a non-trivial solution if Δ = 0
∴ Δ = p₀t³ + p₁t² + p₂t + p₃, p₀, p₁, p₂, p₃ ∈ R.
Hence Δ is cubic polynomial in t.
Hence number of values of t is 3.