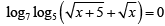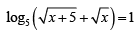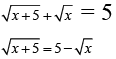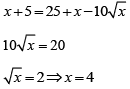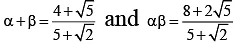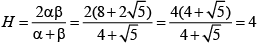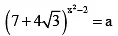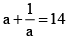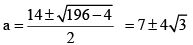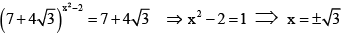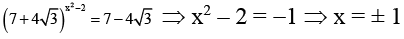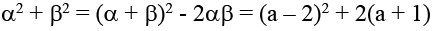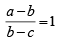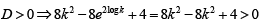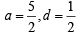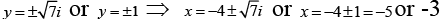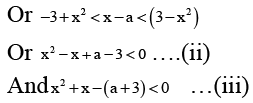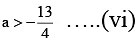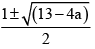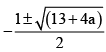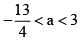Integer Answer Type Questions for JEE: Quadratic Equation & Inequalities | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The solution of the equation 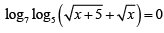 is
is
Ans. 4
Q.2. If x2 + mx + 1 =0 and (b - c) x2 + (c - a) x + (a - b) = 0 have both the roots common, then product of roots is
Ans. 1
x2 + mx + 1 =0 .....(1)
(b - c)x2 + (c - a) x + (a - b) = 0 .....(2)
Note x = 1 satisfies (2)
∴ x= 1 satisfies (1)
Thus 1+ m +1 = 0 ⇒ m = -2
Therefore, (1) becomes x2 - 2x + 1 = 0 ⇒ ( x -1)2 = 0
Thus, two roots of (1) are 1, 1.
∴ Product of roots = 1
Q.3. The harmonic mean of the roots of the equation 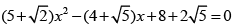 is
is
Ans. 4
Let α, β be the roots the given equation
Then
Let H be harmonic mean of α and β, then
Q.4. If 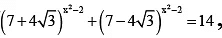 then the positive integral value of x is
then the positive integral value of x is
Ans. 1
Let
⇒
⇒ a2 – 14a + 1 = 0
⇒
∴
&
∴ Positive value of x is 1.
Q.5. The real value of a for which the sum of the squares of the roots of the equation x2 – (a – 2)x – a – 1 = 0 assume the least value is
Ans. 1
Discriminant of the equation is (a – 2)2 + 4(a + 1) = a2 - 4a + 4 + 4a + 4= = a2 + 8 > 0 as a ∈ R
∴ Roots of the equation are real. Let these roots e α and β.
Then α + b = α – 2, αβ = - ( a+1)
We have
= a2 – 4a + 4 + 2a + 2
= a2 – 2a + 6 = (a – 1)2 + 5
Thus, α2 + β2 is least when a = 1.
Q.6. If the roots of the equation (b - c ) x2 + ( c - a ) x + ( a - b) = 0 be equal and a + c= kb . Then the value of k =
Ans. 2
put x = 1
(b – c) + (c – a) + (a – b) =0
so x = 1 is the root by (b – c) x2 + (c – a) x + (a – b) = 0
roots are equal.
products of roots =
a – b = b – c ; ∴ a + c= 2b then k = 2
Q.7. If the product of the roots of the equation 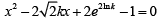 is 31, then the roots of the equation are real for k =
is 31, then the roots of the equation are real for k =
Ans. 4
But k > 0 there fore k = 4
Now
for all k, Hence k = 4
Q.8. Given that a ,g are roots of the equation Ax2 - 4x + 1 = 0 and β ,δ are the roots of the quation Bx2 - 6x + 1 = 0 , if α ,β, γ and δ are in H.P. then find the value of B
Ans. 8
α ,β, γ and δ are in H.P.are in A.P.
a – 3d, a – d, a + d, a + 3d, replacing x by 1/x we get the equation where roots areetc. x2 - 4x + A =0 has roots a – 3d, a + d and x2 - 6x + B =0 has roots a - d, a + 3d.
Sum = 2(a – d) = 4,
2(a + d) = 6
⇒
product = (a – 3d)(a +d) =A =3
(a – d)(a +3d) = B =8
Q.9. The number of real roots of ( x + 3)4 + (x + 5)4 = 16 is
Ans. 2
Put
The equation (1) becomes ( y -1)4 + (y + 1)4 = 16
⇒ 2[y4 + 6y2 +1] =16 ⇒ y4 + 6y2 -7 = 0
⇒ ( y2 + 7)(y2 -1) = 0 ⇒ y2 =-7 or y2 = 1
⇒
Thus, the given equation has two real roots.
Q.10. The number of integral values of a for which the inequality 3 - x - a > x2 is satisfied by at least one negative x, must be equal to
Ans. 6
Given inequality is
3 - |x - a| > x2 ...(i)
⇒ x -a < 3 - x2
If α, β ( α < β) be the real and unequal roots of the corresponding, equation of eq. (i) for all x ∈ (α,β). Since Eq. (i) will have at least one negative solution. The corresponding equation of (ii) and (iii) are
x2 - x + a - 3 = 0 ...(iv)
And x2 + x - (a + 3) = 0 ...(v)
Respectively.
Both eqs. (iv) and (v) should have real and unequal roots, then
1 - 4.1.( a - 3) > 0 and 1 + 4.( a + 3) > 0
i.e.and
Roots of eq. (iv) are
One of these will be negative provided
13 - 4a> 1
i.e. a <3
And roots of eq. (v) are
So, it has one negative root.
Combining eqs. (vi) and (vii), we get
∴ Integral values of a are –3, –2, –1, 0, 1, 2.
Total number = 6
|
446 docs|930 tests
|