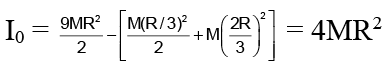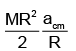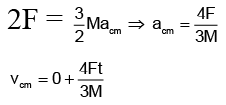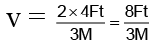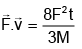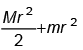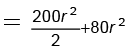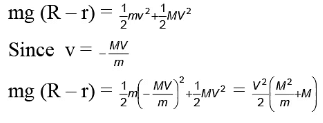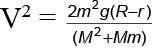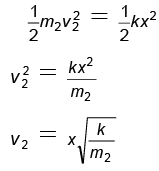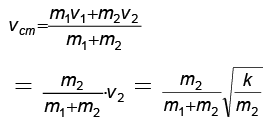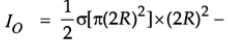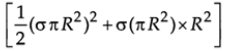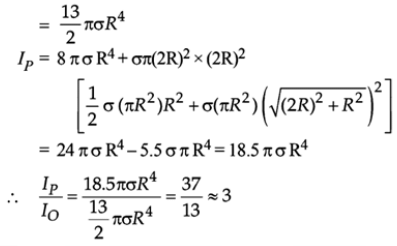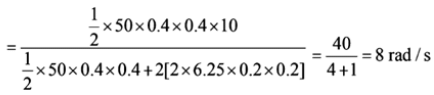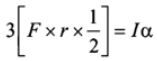Integer Answer Type Questions for JEE: Rotational Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download
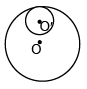
Q.1. A circular disc of radius R/3 is cut from a circular disc of radius R and mass 9 M as shown. Calculate moment of inertia of remaining disc about centre ‘O’ perpendicular to the plane of the disc.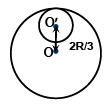
Ans. 4
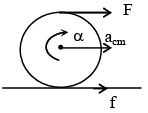
Q.2. A uniform disc of mass M is placed on a rough ground. A force F is applied on the top point at t = 0. Force always remains horizontal. If the disc performs pure rolling then calculate the power developed by the applied force and frictional force as a function of time.
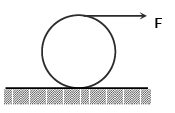
Ans. 0
F + f = Macm ... (1)FR - fR =
⇒ F -f = M/2 acm .... (2)
Solving (1) and (2)
So, velocity of top point at any time
Power developed by applied force =
As velocity of contact point is zero, hence power developed by friction = 0
Q.3. The angular velocity of a body is 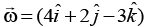 rad/s at some instant of time and torque on the body is
rad/s at some instant of time and torque on the body is 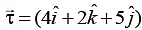 Nm. Power delivered by torque at this instant is
Nm. Power delivered by torque at this instant is
Ans. 20
Watt
Q.4. A wheel whose moment of inertia is 2 kg m2 has an initial angular velocity of 50 rad/s. A constant torque of 10 Nm acts on the wheel. The time in which the wheel is accelerated to 80 rad/s is
Ans. 6
Initial angular velocity = 50 rad/s
Final angular velocity = 80 rad/s
Torque = 10 N-m
Moment of Inertia = 2 kg m2
Angular acceleration α is given by t = Iαα = t/I = 10/2 = 5 rad/s2
Hence if t is the time 5t = 80 - 50 = 30
t = 6 seconds
Q.5. A man of 80 kg is standing on the rim of a circular platform of mass 200 kg. The platform rotates about its axis at 12 r.p.m. The man moves from rim to centre of the platform. How will the system rotate? (The moment of inertia of man at the centre may be neglected.)
Ans. 21.6
If r is the radius of the platform and M its mass,
Moment of inertia of platform about the axis= Mr2/2.
Moment of inertia of the system with the man at the rim =
Moment of inertia with the man at the centre is Mr2/2 = 100
By conservation of angular momentum, 180 r2ω1 = 100 r2ω2= 21.6 rpm
Q.6. A block of mass M = 4 kg with a semicircular track of radius R = 5 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 1m and mass m = 6kg is released from rest at the top point A (see Figure). The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reached the bottom (point B) of the track? How fast is the block moving when the cylinder reaches the bottom of the track? (√2 = 1.4 )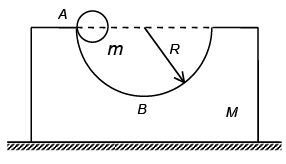
Ans. 840 cm/s
The horizontal component of forces acting on M-m system is zero and the centre of mass of the system cannot have any horizontal displacement.
When the cylinder is at B its displacement relative to the block in the horizontal direction is (R – r). Let the consequent displacement of the block to the left be x. The displacement of the cylinder relative to the ground is (R – r – x).
Since, the centre of mass has no horizontal displacement
M.x = m (R - r - x)
x (M + m) = (R - r)m
x = (R r)m/(M m)
When the cylinder is at A, the total momentum of the system in the horizontal direction is zero. If v is the velocity of the cylinder at B and V, the velocity of the block at the same instant, then mv + MV = 0, by principle of conservation of momentum.
Potential energy of the system at A = mg (R – r)
Kinetic energy of the cylinder at B = 1/2 mv2
The kinetic energy of the block at that instant = 1/2 mv2
By principle of conservation of energy,
V = 840 cm/s
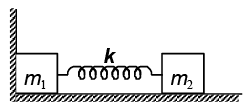
Q.7. Two blocks of masses m1 = 5 kg and m2 = 10 kg connected by a weightless spring of stiffness k = 90 N/m rest on a smooth horizontal plane. Block 2 is shifted a small distance x = 1 m to the left and released. Find the velocity of the centre of mass of the system after block 1 breaks off the wall.
Ans. 2
We know that the potential energy of compression = 1/2 kx2
When the block m1 breaks off from the wall the spring has its unstretched length and the kinetic energy of the block m2 is given by
For the velocity of centre of mass
Velocity of centre of mass of system = 2m/s
Q.8. A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though 0 and P is l0 and lp respectively. Both these axes are perpendicular to the plane of the lamina. The ratio lp/ l0 to the nearest integer is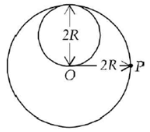
Ans. 3
Let σ be the surface mass density. Then
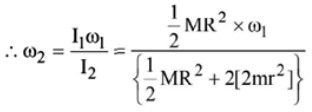
Q.9. A uniform circular disc of mass 50 kg and radius 0.4 m is rotating with an angular velocity of 10 rad s-1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in rad s-1) of the system is
Ans. 8
Applying conservation of angular momentum
I1ω1 = I2ω2
Q.10. A uniform circular disc of mass 1.5 kg and radius 0.5 m is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces, the angular speed of the disc in rad s-1 is
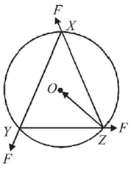
Ans. 2
3 x 0.5 x 0.5 x 1/2 = 1/2 x 1.5 x 0.5 x 0.5 x α
⇒ α = 2 rad s-1
ω = ω0 + αt ⇒ ω = 0 + 2 x 1 = 2 rad s-1
|
446 docs|929 tests
|