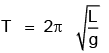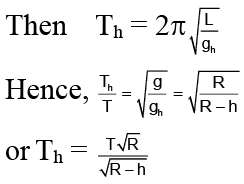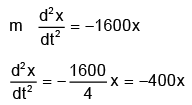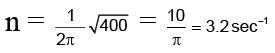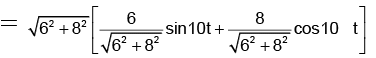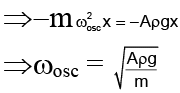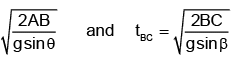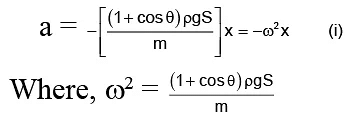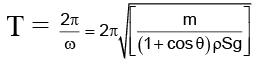Integer Answer Type Questions for JEE: Simple Harmonic Motion (Oscillation) | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. Show that the period of oscillation of simple pendulum at depth h below earth’s surface is inversely proportional to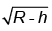where R is the radius of earth. Find out the time period of a second pendulum at a depth R/2 from the earth’s surface?

Ans. 2.8
At earth’s surface the value of time period is given by

Where, L is the effective length of the simple pendulum and g is the acceleration due to gravity and is equal to At depth h if the period is T_h and acceleration due to gravity is g_h,

Thus, Th is inversely proportional to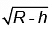 
Time period at h = R/2 is given by

Q.2. A particle of mass 4 gm. lies in a potential field given by V = 200x² + 150 ergs/gm.  Deduce the frequency of vibration.

Ans. 3.2
The potential energy of the 4gm mass U = mV = 4 (200x² + 150) = 800x² + 600 ergs
The force F acting on the particle is given by
= - 1600x
Then the equation of motion of the particle is given by

Hence, frequency of oscillation

Q.3. The equation of a simple harmonic motion is given by x = 6 sin10 t + 8 cos10 t, where x is in cm, and t is in seconds. Find the resultant amplitude.

Ans. 10

x = 6 sin 10 t  + 8 cos 10 t

= 10 sin (10 t + ϕ) where ϕ = tan^-1 (8/6)
∴ Resultant amplitude  = 10 cm.

Q.4. A cubical body (side 0.1 m and mass 0.02 kg) floats in water.  It is pressed and then released so that it oscillates vertically. Find the time period of oscillation. (Density of water = 10³ kg/m³).

Ans. 0.0885
When a floating cubical body is displaced down through a small distance x, the excess buoyant force that is known as the restoring force is given as
F = -vρg
Where v = volume of the excess liquid displaced = Ax
⇒ F = -Aρgx; A = area of cross section of the cube.

m = 0.02 kg,  ρ = 10³ kg/m³,  A = (0.1)² m² .
T = = 0.0885 sec

Q.5. Find the time period of the motion of a particle shown in figure.  Neglect the small effect of the bend near the bottom.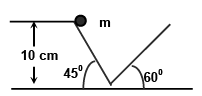

Ans. 0.726
The time of motion for one cycle  = 2 [t_AB + t_BC]
where tAB =
AB = h cosec θ and BC = h cosec β.
H = 0.10 m ,  θ = 45°,  β = 60°
T = 0.726 sec.

Q.6. Determine the period of oscillation of mercury of mass m = 200g poured into a bent tube whose right arm forms an angle q = 30° with the vertical. The crosssectional area of the tube S = 0.50 cm². The viscosity of mercury is to be neglected.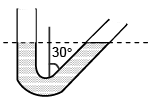

Ans. 0.8
The difference of level in the two tubes is given by

= x + xcosθ = x (1+cosθ)
The change in pressure ΔP is given by
ΔP = x (1+cosθ) ρg
Force F = ma = - [x (1+cosθ) ρg]S

Equation (i) is the equation of S.H.M. It’s time period T is given by

Substituting the given values, we get
T = 2 x 3.14 = 0.8 sec.

Q.7. The length of a sonometer wire between its fixed ends is 110 cm. Where two bridges should be placed in between the ends so as to divide the wire into 3 segments whose fundamental frequencies are in the ratio 1: 2: 3?

Ans. 20, 30, 60

If L₁, L₂, L₃ be the lengths of the three segments then
L₁ + L₂ + L₃ = 100

If n₁, n₂ and n₃ be the fundamental frequencies of the three segments then
f₁ = f
f₂ = 2f
f₃ = 3f,
Since, f₁: f₂: f₃ = 1: 2: 3
The tension remains the same throughout the wire. Hence
f₁L₁ = f₁L₂ = f₃L₃ 
or,  fL₁ = 2fL₂ = 3fL₃ 
or, L₁ = 2L₂ = 3L₃ 
If L₃ = x, L₂ = 3/2x, L₁ = 3x
∴ L₁ + L₂ + L₃ = 3x + 3/2 x + x = 110 cm       

or,   11x = 220 cm
L₃ = x =   20 cm
L₂ = 3/2 x = 30 cm
L₁ = 3x = 60 cm
The bridges should be placed in the positions of 54.54 cm from the zero end and 18.18 cm from the other end.