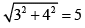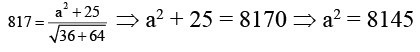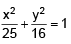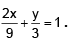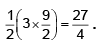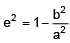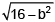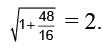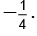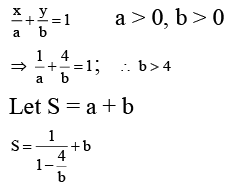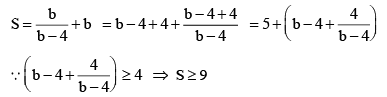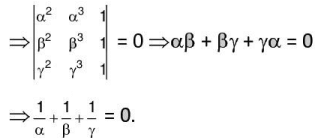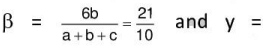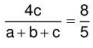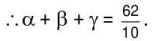Integer Answer Type Questions for JEE: Straight Lines & pair of Lines | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Tangents are drawn to the circle x2 + y2 + 6x + 8y- 12 = 0 from origin. Determine the diameter of the circle passing through the points of contact of the tangents and the origin.
Ans. If P, Q be the points of contact of tangents drawn from (0, 0) then PQ is chord of contact whose equation is 3(x + 0) + 4(y + 0) – 12 = 0 or 3x + 4y – 12 = 0
∴ Required circle by S + λP = 0 is
(x2 + y2 + 6x + 8y – 12) + λ (3x + 4y – 12) = 0
Since it passes through (0, 0)
∴ λ = –1
∴ Circle is x2 + y2 + 3x + 4y = 0
Hence, its diameter = 5
Aliter: By geometry the diameter = dist. between the centre of given circle and origin =
Q.2. A circle passes through the point (3, 4) and cuts the circle x2 + y2 = a2 orthogonally. The locus of its centre is a straight line. If the distance of the straight line from the origin is 817, then find the value of a2 - 8140.
Ans. Let the equation of the circle be x2 + y2 + 2gx + 2fy + c = 0.
Since it passes through (3, 4),
6g + 8f + c = -25. At it cuts the circle x2 + y2 = a2
orthogonally
2g × 0 + 2f × 0 = c - a2 ⇒ c = a2 ⇒ 6g + 8f + a2 + 25 = 0
Locus of the centre (-g, -f) is 6x + 8y - (a2 + 25) = 0
Distance of the line from the origin is
Q.3. F1 and F2 are two points situated at (3, 0) and (-3, 0) respectively. If P(x, y) is a point on the curve 16x2 + 25y2 = 400, then PF1 + PF2 is equal to
Ans. The given curve is
which is an ellipse so that a = 5, b = 4⇒ 16 = 25 (1 - e2)
⇒ e = 3/5.We find that ae = 3.
Hence, F1((3, 0) and F2(-3, 0) are the foci of the given ellipse.We know that PF1 + PF2 = 2a = 10.
Q.4. Tangents are drawn to the ellipse 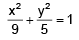 at the ends of the latus recta. The area of the quadrilateral thus formed is
at the ends of the latus recta. The area of the quadrilateral thus formed is
Ans. The coordinates of the extremity of one of the latus recta are P(2, 5/3).
The equation of the tangent to the given ellipse at P is
It meets the coordinate axis at T(9/2, 0) and R(0, 3). If C is the centre of the ellipse then the area of the triangle CTR =
The area of the quadrilateral formed by the four tangents is thus 27.
Q.5. If the foci of the hyperbola 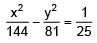 coincide, with the ellipse
coincide, with the ellipse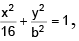 at the ends of the latus recta. The area of the quadrilateral thus formed is
at the ends of the latus recta. The area of the quadrilateral thus formed is
Ans.
and foci are (–3, 0) and (3, 0).
Now eccentricity of the ellipse is 'e' so that
⇒ e2 a2 = a2 – b2 ⇒ ea = ±
⇒ 16 – b2 = (3)2 ⇒ b2 = 7.
Q.6. The locus of the points of intersection of the lines √3x - y - 4√3t = 0 and √3tx + ty - 4√3 = 0, for different values of t is a curve of eccentricity equal to
Ans. We have √3x - y - 4√3t
√3tx - ty - 4√3t
Squaring and adding we get
3(1 + t2)x2 = (1 + t2)y2 + 48(t2 + 1)which is a hyperbola whose eccentricity is e =
Q.7. If the line x + y –1 = 0 touches the parabola y2 = kx, then the value of k is
Ans. Any tangent to y2 = kx is y = mx + k/m.
Comparing it with given line y = 1 - x, we get, m = -1 and k/4m = 1 ⇒ k = -4.
Alternative:
If x+ y –1 = 0 touches y2 = kx, then y2 = k(1-y) would have equal roots
⇒ k2 + 4k = 0
⇒ k = 0 or -4. But k ≠ 0 , hence k = -4.
Q.8. If the point P(4, –2) is the one end of the focal chord PQ of the parabola y2 = x , then the slope of the tangent at Q is
Ans. The equation of the tangent at (4, –2) to y2 = x is
– 2y = 1/2 (x + 4) or x + 4y + 4 = 0.
Its slope is
Therefore the slope of the perpendicular line is 4. Since the tangents at the end of focal chord of a parabola are at right angle, the slope of the tangent at Q is 4.
Q.9. A straight line with negative slope passing through the point (1, 4) meets the coordinate axes at A and B find the least value of OA + OB.
Ans.
Q.10. The co-ordinates of the extremities of one diagonal of a square are (1, 1) and (-2, -1). If the equation of the other diagonal is 6x + 4y + λ = 0. The numerical quantity λ must be equal to
Ans. The diagonals of the square bisect each other.
Midpoint of the diagonal with end-point (1, 1), (-2, -1)
must lie on the other diagonal given by 6x + 4y + λ = 0
i.e.satisfies 6x + 4y + λ = 0
⇒ -3 + 0 + λ = 0 ⇒ λ = 3
Q.11. Let P(α1, β1), Q(α2, β2) and R(α3, β3) be the centroid, orthocentre and circumcentre of a scelene triangle having its vertices on the curve y2 = x3, then 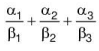 is equal to________.
is equal to________.
Ans. Let P, Q and R be (α2, α3), (β2, β3) and (γ2, γ3)
Q.12. The lengths of the tangents drawn from the vertices A, B, C to the incircle of ΔABC are 5, 3, 2 respectively. If the lengths of the parts of tangents within the triangle which are drawn parallel to the sides BC, CA, AB of the triangle to the incircle be α, β, γ respectively then 10(α + β + γ) -60 equals____________.
Ans. Given s- a=5 , s - b = 3, s - c = 2 ⇒ s = 10 and a = 5, b = 7 and c = 8
now length of tangent from A to incircle = semiperimeter of ΔAPQ(∵ ΔAPQ and ΔABC are similar)
similarly
Q.13. Two consecutive sides of a parallelogram are 4x + 5y = 0 and 5y - 8x = 0. If the equation of one diagonal is 14x - 5y - 9 = 0. Find slope of other diagonal
Ans. 2
Q.14. Eliminating y, the x coordinate of point of intersection is given by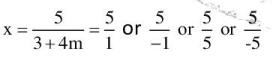
Ans. 1
because x is also an integer
∴ 3 + 4 m = 1 , - 1 , 5 o r -5
or 4m =-2,-4,2,-8
Q.15. Two points (a, 3) and (5, b) are the opposite vertices of a rectangle. If the other two vertices lie on the line y = 2x + c which passes through the point (a, b) then value of c is -k, where k=........
Ans. 7
|
446 docs|929 tests
|