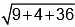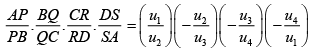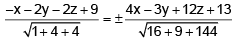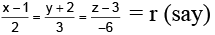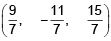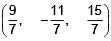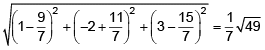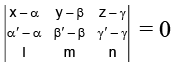Integer Answer Type Questions for JEE: Three dimensional Geometry | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. The distance of the point (-1, 2, 6) from the line 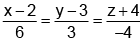,  is equal to:

Ans. 7
Any point on the line is P = (6r₁ + 2, 3r₁ + 3, –4r₁ –4).
Direction ration of the line segment PQ, where Q = (–1,  2,  6),are 6r₁ + 3, 3r₁ + 1, – 4r, – 10.
If ‘P’ be the foot of altitude drawn from Q to the given line, then
6(6r₁ + 3) + 3(3r₁ + 1) + 4(4r₁ + 10) = 0.
⇒ r₁ = –1.
Thus, P = (–4, 0, 0)
∴ Required distance =
= 7 units

Q.2. The shortest distance between the line x + y + 2z – 3 = 2x + 3y + 4z – 4 = 0 and the z-axis is:

Ans. 2
We have,
x + y + 2z -3 = 0, x + 2z - 2 +3/2 y = 0
Solving these equations, we get Y = –2.
Thus, required shortest distance is 2 units

Q.3. The equation of the plane containing the line 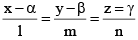 is a (x - α) + b (y - β) + c (z -γ) = 0, where al + bm + cn is equal to 

Ans. 0
Since, straight line lies in the plane so it will be perpendicular to the normal at the given plane.
Since, direction cosines of straight line are l, m, n and direction ratio of normal to the planes are
a, b, c. So, al + bm + cn = 0.

Q.4. If d is the distance between the point (-1, -5, -10) and the point of intersection of the line 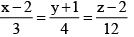 with the plane x – y + z = 5, then d – 10  is equal to

Ans. 3
Any point on the line is (3r + 2, 4r – 1, 12r + 2) which lies on the plane if
3r + 2 – (4r – 1) + 12r + 2 = 5
⇒ r = 0 and the point of intersection of the line and the plane is (2, -1, 2).
So, d² = (2 + 1)² + (-1 + 5)² + (2 + 10)² = 169
⇒ d = 13  ⇒ d -10 = 3

Q.5. P, Q, R, S are four coplanar points on the sides AB,BC,CD,DA of a skew quadrilateral. ABCD. The product equals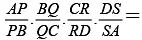

Ans. a
Let the vertices A,B,C,D of quadrilateral be  and  and the equation of plane.
PQRS be u = ax + by + cz + d = 0
Let u_r = a_r x + b_r y + c_r z + d where r = 1, 2, 3, 4
Then
= 1

Q.6. Show that the origin lies in the acute angle between the planes x + 2y + 2z - 9 = 0 and 4x - 3y + 12z + 13 = 0. Find the plane bisecting the angle between them and distinguish the acute angle bisector. 

Ans. 3
- x - 2y - 2z + 9 = 0 .....(1)
And 4x - 3y + 12z + 13 = 0 ....(2)
So, a₁a₂ + b₁b₂ + c₁c₂ = (-1) . 4 + (-2). (-3) + (-2) . 12 = negative
Hence, origin lies in the acute angle between plane (1) and (2)
The equation of bisector planes between the given planes are
⇒ 25x + 17y + 62z - 78 = 0 ....(3)  
⇒ x + 35y - 10z - 156 = 0 ....(4)
As origin lies in acute angle so acute angle bisector will be represented by (3).

Q.7. Find the distance of the point (1, –2, 3) from the plane x – y + z = 5 measured parallel to the line .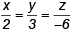

Ans. 1
Here we are not to find perpendicular distance of the point from the plane but distance measured along with the given line. The method is as follow: The equation of the line through the point (1, –2, 3) and parallel to given line is
The coordinate of any point on it is (2r + 1, 3r – 2, –6r + 3).
If this point lies in the given plane then
2r + 1 – (3r – 2) + (–6r + 3) = 5  
⇒ –7r = –1 or r = 1/7
∴ Point of intersection is
∴ The required distance = the distance between the points (1, –2, 3) and
=
= 1 unit.

Q.8. Find the equation of the plane through the point (α', β', γ') and the line .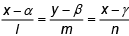

Ans. 0
The equation of any plane through the given line is
a(x - α) + b(y - β) + c(z - γ) = 0 ....(1) where  al + bm + cn = 0 ....(2)
The plane (1) passes through the point (α', β', γ') so a(α' - α) + b(β' - β) + c(γ' - γ) = 0 ...(3)
The equation of the required plane will be obtained by eliminating a, b, c between the equation (1), (3) and (2).
Hence, eliminating a, b, c between the above equations, the equations of the required plane is given by

or ∑(x - α){n(β' - b) - m(γ' - γ)} = 0.

Q.9. The shortest distance between the two straight lines 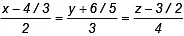 and .

Ans. 0
Since these two lines are intersecting so shortest distance between the lines will be 0.

Q.10. A plane is passed through the middle point of the segment A(–2, 5, 1), B(6, 1, 5) and is perpendicular to this line. Then its equation is _____________.

Ans. 4
Plane passes through the midpoint of AB and direction ratio of normal to plane is proportional to direction ratio of AB. So equation of plane is
(6 + 2)(x - 2) + (1 - 5)(y - 3) + (5 - 1)(z - 3) = 0
8x - 4y + 4z = 16
2x - y + z = 4.