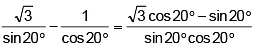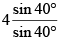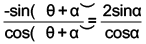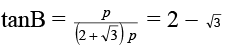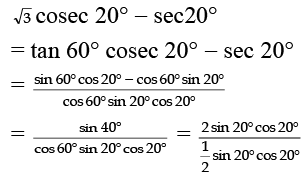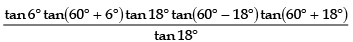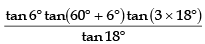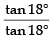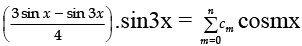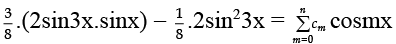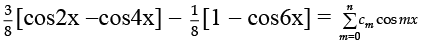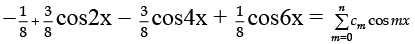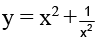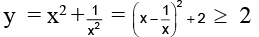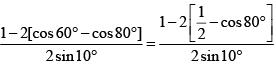Integer Answer Type Questions for JEE: Trigonometric Equations & Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. √3 cosec20° - sec20° =

Ans. 4
Given =
=  = 4.
=
= 4

Q.2. If sinθ = 3sin(θ + 2α), then  the value  of tan (θ + α) + 2tanα is:

Ans. 0
Given sin θ = 3sin (q + 2αa)
⇒ sin (θ + α - α) = 3sin (θ + α + α)
⇒ sin (θ + αa) cosα - cos(θ + α) sinα
=  3sin (θ + α) cosαa + 3cos (θ + α) sinα
⇒ -2sin (θ + α) cosα = 4cos (θ + α) sinα
⇒
⇒ tan(θ + a) + 2tanα = 0

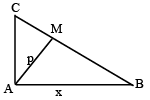
Q.3. In a right angled triangle, the hypotenuse is four times as long as the perpendicular drawn to it from the opposite vertex. One of the acute angles is

Ans. 15

Let AM be perpendicular from A on BC such that AM = p.
Then BC = 4p. Let AB = x, AC = y.
Then x² + y² = (4p)².
In ΔABM, p² + BM² = x²
Adding (i) and (ii), 2p² + (4p -k²) = x² + y²
⇒ 2p² + (4p - k²) = (4p)²
⇒ k = 2p - √3 p
∴ BM = BC - CM = 4p - (2p - √3p) = 2p + √3 p
⇒
⇒ B = 15°

Q.4. The value of √3 cosec 20° - sec20° is equal to

Ans. 4

= 4

Q.5. The value of tan 6° tan 42° tan 66° tan 78° is

Ans. 1
We have, tan 6° tan 42° tan 66° tan 78°
= tan 6° tan(60° - 18°) tan(60° + 6°) tan(60° + 18°)
=
=
=
=
= 1

Q.6. Suppose that 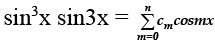is an identity in x, where c₀, c₁, c2, …. , c_n are constants and c_n ≠ 0, find the value of n.

Ans. 6
[Express L.H.S. in multiple of x and compare with R.H.S.].
Given
or,
or,
or,
or,
Comparing, we get n = 6.
[Q Highest multiple of angle on L.H.S. is 6x and on R.H.S. is nx].

Q.7. The  number  of  all possible  5-tuples (a₁, a₂, a₃,, a₄, a₅ ) such  that  a₁ +a₂sinx +a₃cosx +a₄ sin2x +a₅cos2x = 0  holds   for  all   x  is 

Ans. 1
Since the equation a₁ +a₂sinx + a₃cosx + a₄ sin2x + a₅ cos2x = 0 holds for all values of x,
a₁+ a₃ + a₅ = 0 ( on putting x = 0)
a₁- a₃ + a₅ = 0   ( on putting   x = π)
⇒ a₃  = 0 and  a₁ + a₅ =0 . . . .   (1)
Putting   x = π/2  and 3π/2,  we get
a₁ + a₂ -  a₅= 0  and a₁ -  a₂ - a₅ = 0
⇒ a₂ = 0 and  a₁ – a₅ = 0 . . . .   (2)
(1)  and (2)  give
a₁ = a₂ = a₃ = a₅ = 0.
The given equation reduces to a4sin2x  = 0 . This is true   for all values  of x ,  therefore a₄ = 0
Hence  a₁ = a₂ = a₃ = a₄ = a₅ = 0.
Thus, the number of 5-tuples is one.

Q.8. The number of solution of 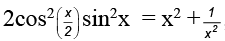,0 ≤ x ≤ π/2 is 

Ans. 0
We have  is
Let
⇒ y = (1+ cosx) sin² x and
when  y = (1+ cosx) sin² x = (a number < 2) (a number ≤ 1)
⇒ y < 2 . . . .  (1)
and  when
⇒ y ≥ 2 . . . .  (2)
No value of y can be obtained satisfying (1) and (2), simultaneously
⇒ No real solution of the equation exists.

Q.9. If sinθ = 3sin(θ + 2α), then  the value  of tan (θ + α) + 2tanα is:

Ans. 0
Given sin θ = 3sin (q + 2αa)
⇒ sin (θ + α - α) = 3sin (θ + α + α)
⇒ sin (θ + αa) cosα - cos(θ + α) sinα
=  3sin (θ + α) cosαa + 3cos (θ + α) sinα
⇒ -2sin (θ + α) cosα = 4cos (θ + α) sinα
⇒
⇒ tan(θ + a) + 2tanα = 0

Q.10. The value of the expression 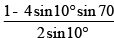 is

Ans. 1
Given expression is
=
=
= 1