Integration by Parts | Mathematics (Maths) Class 12 - JEE PDF Download
Definition
dx where u & v are differentiable functions.
Note : While using integration by parts, choose u & v such that
(a) dx v is simple &
(b) dx is simple to integrate.
This is generally obtained, by keeping the order of u & v as per the order of the letter in ILATE, where
I – Inverse function
L – Logarithmic function
A – Algebraic function
T – Trigonometric function
E – Exponential function
Remember This:
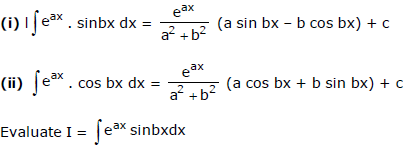
Proof:
Integrating by parts taking sin bx as the second function,
Again integrating by parts taking cos bx as the second function, we get
Transposing the term -a2/b2 I to the left hand side, we get
Solved Examples
Ex.1 Integrate xn log x
Sol.
Ex.2 Evaluate dx
Sol.
Put sec–1 x = t so that
Then the given integral =
= t (log t – log e) + c = sec–1 x (log (sec–1 x) – 1) + c
Ex.3 Evaluate dx.
Sol.
Put x = cos θ so that dx = - sin θ dθ. the given integral
Ex.4 Evaluate
Sol.
We have
[ x3 = x(x2 + 1) - x]
integrating by parts taking x2 as the second function
Ex.5 Evaluate dx.
Sol.
(put, 2x + 2 = 3 tanθ ⇒ 2 dx = 3 sec2θ dθ )
Ex.6 If
Sol.
Ex.7 Evaluate
Sol.
Ex.8 Evaluate
Sol.
x where f(x) = tan x = ex f(x) + c = ex tanx + c
Ex.9 Evaluate
Sol.
using, previous example
|
203 videos|307 docs|139 tests
|
FAQs on Integration by Parts - Mathematics (Maths) Class 12 - JEE
| 1. What is integration by parts? |  |
| 2. How does integration by parts work? |  |
| 3. When should integration by parts be used? |  |
| 4. Can integration by parts be used multiple times? |  |
| 5. What are some common mistakes to avoid when using integration by parts? |  |
















