Integration by Substitution & Trigonometric Identities | Mathematics (Maths) Class 12 - JEE PDF Download
1. Integration by Substitution
Let g be a function whose range is an interval l, and let f be a function that is continuous on l. If g is differentiable on its domain and F is an antiderivative of f on l, then f(g(x))g'(x) dx = F(g(x)) + C.
If u = g(x), then du = g'(x) and f(u) du = F(u) + C .
Guidelines for making a change of variable
1. Choose a substitution u = g(x). Usually, it is best to choose the inner part of a composite function, such as a quantity raised to a power.
2. Compute du = g'(x) dx.
3. Rewrite the integral in terms of the variable u.
4. Evaluate the resulting integral in terms of u.
5. Replace u by g(x) to obtain an antiderivative in terms of x.
The General Poser Rule for Integration
If g is a differentiable function of x, then
Rationalizing Substitutions
Some irrational functions can be changed into rational functions by means of appropriate substitutions.
In particular, when an integrand contains an expression of the form then the substitution u =
may be effective.
Some Standard Substitutions
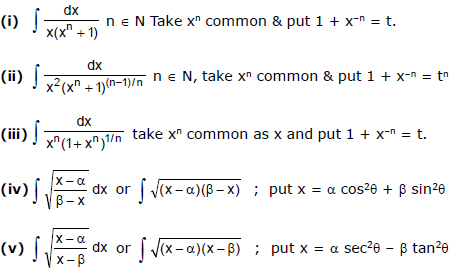
2. Integration Using Trigonometric Identities
In the integration of a function, if the integrand involves any kind of trigonometric function, then we use trigonometric identities to simplify the function that can be easily integrated.
Few of the trigonometric identities are as follows:
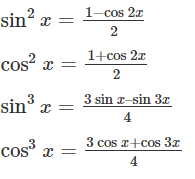
All these identities simplify integrand, that can be easily found out.
Solved Examples:
Ex.1 Evaluate (x2 +1)2 (2x) dx .
Sol. Letting g(x) = x2 + 1, we obtain g'(x) = 2x and f(g(x)) = [g(x)]2.
From this, we can recognize that the integrand and follows the f(g(x)) g'(x) pattern. Thus, we can write
Ex.2 Evaluate
Sol.
Ex.3 Evaluate
Sol.
Let u = x4 + 2 ⇒ du = 4x3 dx
Ex.4 Evaluate
Sol.
Let u = x3 – 2. Then du = 3x2 dx. so by substitution :
Ex.5 Evaluate
Sol. Let u = . Then u2 = x + 4, so x = u2 –4 and dx = 2u du.
Therefore
Ex.6 Evaluate
Sol. Rewrite the integrand as follows :
= – ln (e-x + 1) + c (∴ e-x + 1 > 0)
Ex.7 Evaluate sec x dx
Sol. Multiply the integrand sec x by sec x + tan x and divide by the same quantity :
Ex.8 Evaluate cos x (4 - sin2 x) dx
Sol. Put sin x = t so that cos x dx = dt. Then the given integral =
Ex.9 Integrate
(i)
(ii)
Sol.
Ex.10 Integrate
(i)
(ii)
Sol.
Ex.11 Integrate
(i)
(ii)
Sol.
Ex.12 Integrate
Sol.
Ex.13 Integrate cos5x.
Sol.
[put sin x = t ⇒ cos x dx = dt]
Ex.14 Evaluate
Sol.
Ex.15 Integrate 1/(sin3 x cos5x).
Sol. Here the integrand is sin–3 x cos–5x. It is of type sinm x cosn x,where m + n = –3 –5 = –8 i.e., –ve even integer
Now put tan x = t so that sec2 x dx = dt
Ex.16 Integrate
Sol. Here the integrand is of the type cosm x sinnx. We have m = –3/2, n = – 5/2, m + n = – 4 i.e., and even negative integer.
,putting tan x = t and sec2x dx = dt
Ex.17 Evaluate
Sol.
Put x – β = y ⇒ dx = dy
Given integral
Now put sinθ + cosθ tan y = z2 ⇒ cosq sec2 y dy = 2z dz
Ex.18 Evaluate dx
Sol.
|
223 videos|377 docs|167 tests
|
FAQs on Integration by Substitution & Trigonometric Identities - Mathematics (Maths) Class 12 - JEE
| 1. What is integration by substitution? |  |
| 2. How do you perform integration by substitution? |  |
| 3. What are trigonometric identities used for in integration? |  |
| 4. How can trigonometric identities be applied in integration? |  |
| 5. Can integration by substitution and trigonometric identities be used together? |  |

















