Integration of Irrational Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Definition |

|
| Solved Examples |

|
| Integrals of the type where x & y are linear or quadratic expressions |

|
| Integration Of A Binomial Differential |

|
Definition
Certain types of integrals of algebraic irrational expressions can be reduced to integrals of rational functions by a appropriate change of the variable. Such transformation of an integral is called its rationalization.
- If the integrand is a rational function of fractional powers of an independent variable x, i.e. the function R
then the integral can be rationalized by the substitution x = tm, where m is the least common multiple of the numbers q1, q2, ...., qk.
- If the integrand is a rational function of x and fractional powers of a linear fractional function of the form
then rationalization of the integral is effected by the substitution
where m has the same sense as above.
Solved Examples
Ex.1 Evaluate
Sol.
Rationalizing the denominator, we have
Ex.2 Evaluate I =
Sol. The least common multiple of the numbers 3 and 6 is 6, therefore we make the substitution
x = t6, dx = 6t5 dt.
Ex.3 Evaluate I =
Sol. The integrand is a rational function of therefore we put 2x – 3 = t6, whence
Returning to x, we get
Ex.4 Evaluate
Sol.
Let x = t3 ⇒ dx = 3t2 then
Ex.5 Evaluate I =
Sol. The integrand is a rational function of x and the expression therefore let us introduce the substitution
Integrals of the type 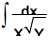 where x & y are linear or quadratic expressions
where x & y are linear or quadratic expressions
Ex.1 Integrate
Sol.
Put 4x + 3 = t2, so that 4dx = 2tdt and (2x + 1)
Ex.2 Evaluate
Sol.
Put (x + 2) = t2, so that dx = 2t dt, Also x = t2 – 2.
∴
dividing the numerator by the denominator
Ex.3 Integrate
Sol.
Put (x + 1) = t2, so that dx = 2t dt. Also x = t2 – 1.
Ex.4 Integrate
Sol.
Put (1 + x) = 1/t, so that dx = – (1/t2) dx.
Also x = (1/t) – 1.
Ex.5 Evaluate
Sol.
Put x = 1/t, so that dx = – (1/t2) dt.
∴
Now put 1 + t2 = z2 so that t dt = z dz. Then
[∵ t = 1/x]
Ex.6 Evaluate I =
Sol.
Integration Of A Binomial Differential
The integral where m, n, p are rational numbers, is expressed through elementary functions only in the following three cases :
Case I : p is an integer. Then, if p > 0, the integrand is expanded by the formula of the binomial; but if p < 0, then we put x = tk, where k is the common denominator of the fractions and n.
Case II : is an integer. We put a + bxn = tα, where α is the denominator of the fraction p.
Case III :+ p is an integer we put a + bxn = tαxn, where a is the denominator of the fraction p.
Ex.1 Evaluate I =
Sol.
Here p = 2, i.e. an integer, hence we have case I.
Ex.2 Evaluate I =
Sol.
i.e. an integer.we have case II. Let us make the substitution. Hence ,
Ex.3 Evaluate I =
Sol.
Here p = – 1/2 is a fraction, m+1/2 = -5/2 also a fraction, but m+1/n + p/2 = -5/2 -1/2 = -3 is an integer, i.e. we have case III, we put 1 + x4 = x4/2,
Hence
Substituting these expression into the integral, we obtain
Returning to x, we get I =
|
177 videos|618 docs|160 tests
|
FAQs on Integration of Irrational Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What are binomial differentials? |  |
| 2. How do you integrate a binomial differential? |  |
| 3. What are some examples of integrating binomial differentials? |  |
| 4. Are there any special cases when integrating binomial differentials? |  |
| 5. Can binomial differentials involve irrational functions? |  |
















