CAT Logical Connectives : Basic Concepts and Notes PDF
Importance of Logical Connectives
- Logical connective questions form an integral part of many competitive exams. Logical connectives questions are part of the logical reasoning section of an aptitude test. They are designed to test your analytical and logical skills.
- Logical connectives questions in your CAT exam can be a high-scoring section if you master the techniques to solve such tricky questions and practice well.
What are Logical Connectives?
A logical connective (also called a logical operator) is a symbol or a word which is used to connect two or more sentences. Each logical connective can be expressed as a truth function.

Logical Connectives
- NOT (Negation)
- AND (Conjunction)
- EITHER OR (Disjunction)
- IF-THEN (Material Implication)
- In logical reasoning, we deal with statements that are essentially sentences in the English language. However, factual correctness is not important.
- We are only interested in the logical truthfulness of the statements. We can represent simple statements using symbols like p and q.
- When simple statements are combined using logical connectives, compound statements are formed.
Types of Topics
The types of logical connective test questions include:
| Topic | Description |
| If, then | Statements in the form of [If A, then B] or [A if B] |
| Only if/when | Statements in the form of [Only If A, then B], or [A, only if B] |
| If and only if | Sentences with a union of sentences with connectives If and only If |
| Unless | Statements in the form of [Unless A, B] or [A, unless B] |
| Either or | Statements in the form of [either A or B] |
1. Negation - NOT
Negation is the opposite of a statement. For example,
(a) Statement: It is raining.
(b) Negation: It is NOT raining.
2. Disjunction - EITHER OR
When two statements are connected using OR, at least one of them is true. For example,
Either p or q: p alone is true; q alone is true; both are true
In such situation, valid inference is If p did not happen, then q must happen. And If p did not happen, then p must happen.
3. Conjunction - AND
When two statements are connected using AND, both statements have to be true for compound statement to be true.
p and q: p should be true as well as q should be true
4. Material Implication - IF THEN
If p, then q (p --> q): It is read as p implies q.
It means that if we know p has occured, we can conclude that q has occured. In such situations, only valid inference is "If ~q, then ~p"; If q did not happen, then p did not happen.
5. Negation of Compound Statements
Negation (p OR q) is same as Negation p AND Negation q
Negation (p AND q) is same as Negation p OR Negation q
Negation (p --> q) is same as Negation p --> Negation q
Logical Connective (If, then)
These statements are in the form of( If p, then q) or( q if p).
Examples-
- If it rains then ground gets wet.
- Raman will pass if he works hard.
Cause-effect relation – In these statements, cause is a sufficient condition for effect to happen but not a necessary condition.
Let’s discuss example 1 in detail – If it rains then the ground gets wet.
In this statement firstly we’ll identify the cause and effect. “It rains is the cause and ground gets wet is the effect.
Now we’ll make all possible cases for understanding it clearly.
Case1. If cause is happening, it means it is raining so obviously ground gets wet (given).
So if cause (yes) then effect (yes).
Case2. If the cause is not happening, it means it's not raining so we have no idea about the condition of the ground because it may be wet or not. It can get wet by some other cause also, we don’t know about that cause.
So if cause (No) then effect (may or may not be)
Case3. If effect is happening, it means ground gets wet but we don’t know how it gets wet. We have no idea about exact cause so cause may be or may not be happened.
So if effect (Yes) then cause (may be or may not be)
Case4. If the effect is not happening, it means the ground does not get wet so we can clearly say that it has not rained because if it had rained the ground would definitely got wet.
So if effect (No) then cause is surely (No).
We can see that in this example we can say surely only in two cases (case1 & case4).
If we draw a conclusion for If and then connectives.
Conclusion (If, then):-
- Cause – yes; effect – yes
- Cause –no; effect -?
- Effect –yes; cause -?
- Effect –no; cause –no
In these type of statements we have SINGLE EFFECT and MULTIPLE CAUSES like ground gets wet is one effect causes may be many like rain, bucket of water etc.
Note: Sometimes instead of ‘if’ when, whenever, everytime these connectives are used but result will be same in these cases also because meaning of statement doesn’t changes.
Logical Connective (only if/when)
These statements are in the form of (Only If p, then q) or (q, only if p).These type of connectives are very important from exam point of view.
Some examples are like
- I will meet you only if I come to Delhi.
- Only if Rohit runs fast, he will catch the train.
Now first we’ll identify the cause and effect
- Come to Delhi – cause; meet you- effect
- runs fast – cause; catch the train- effect
Cause-effect relation – In these statements cause is a necessary condition for effect to happen but not sufficient condition.
Let’s discuss example 2 in detail – . Only if Rohit runs fast, he will catch the train.
Case1– cause yes, it means Rohit runs fast so it doesn’t mean that he will suerly catch the train. Cause – yes; effect- may be may not be
Case2 – cause no, it means Rohit doesn’t run fast so according to statement he will catch the train only if he runs fast so surely he will not catch the train.
Cause- no; effect- no
Case3 – effect yes, it means Rohit catches the train so surely we can say he ran fast.
Effect- yes; cause- yes.
Case-4 – effect no, it means he doesn’t catch the train this doesn’t implies that he didnot ran fast may be due to some other reason he was not able to catch the train.
Effect- no; cause – may be may not be
Conclusion (only if):-
- Cause – yes; effect- ?
- Cause – no; effect- no
- Effect – yes; cause- yes
- Effect – no; cause-?
In this type of statement there is a SINGLE CAUSE and MULTIPLE EFFECTS like running fast is a cause he can catch the train cannot catch the train these are effects.
Note: Instead of if,( when) also occur sometimes but the situation remains same.
Logical Connective (If and Only If)
These type of sentences are union of sentences having connectives If and only If. These are the simplest in all connectives. It is like necessary and sufficient condition which means cause is a necessary and sufficient condition for effect to take place.
Examples:
- If and only If he clears the pre exam, he will get selected.
- Rahul will eat the fruit If and only If it is an apple.
- A whole number is even If and only If its square is even.
Cause-effect relation – In these statements cause is a necessary and sufficient condition for effect to happen.
Let’s discuss all possible cases for example 1 – If and only If he clears the pre exam, he will get selected.
Cause – clears the pre exam, effect – get selected
Case1. Cause is happening it means he cleared pre exam so surely he will get selected because given is ‘if he clears exam he will get selected’.
Cause –yes; effect – yes
Case2. Cause is not happening it means he has not cleared pre exam so surely he will not get selected.
Cause-no; effect-no
Case3. Effect is happening it means he selected it implies surely he has cleared his pre exam.
Effect – yes; cause – yes
Case4. Effect is not happening it means he has not selected .By the statement ‘only if he clears the pre exam he will get selected’ we can say that he not selected means he has not cleared pre exam.
Effect – No; cause-no
Conclusion (If and only If):-
- Cause – yes; effect – yes
- Cause – no; effect – no
- Effect – yes; cause- yes
- Effect – no; cause – no
In these type of statements cause is necessary and sufficient condition for effect.
Note: Instead of (If and only If) connectives (until and unless) and (when and only when) cn also be used for similar conditions. Results will remain same.
Logical Connective (unless)
These statements are in the form of (Unless p, q) or (q, unless p). These type of connectives do not have that much importance for exams but it is better to understand the concept. It is a negative type of connective which gives negative sense in the statement. In these statements there is no proper cause and effect. Only two statements are there in these type of statements.
Examples:
- Unless I’m mistaken, John’s house is the second on the left.
- Unless Virat is the captain, India will lose the match.
Let’s discuss example 2 in detail – . Unless Virat is the captain, India will lose the match.
Here No cause and effects is present because it is negative statement. We can check using statements 1 and 2 directly. Virat is the captain (1) & India lose the match (2).
Case1. If 1 is true it means Virat is the captain it doesn’t mean that India will surely win the match so we can’t say anything.
(1) – yes, (2) – may be may not be
Case2. If 1 is false it means Virat is not the captain it means surely India will lose the match.
(1) – no, (2) – yes
Case3. If 2 is true it means India lose the match so we can’t say anything that Virat is the captain or not. India can also lose the match when Virat is captain.
(2) – yes, (1) – may be may not be
Case4. If 2 is not true it means India won the match so we can surely say that Virat is the captain.
(2) – no, (1) – yes
Conclusion (unless):-
(1) – yes; (2) – ?
(1) – no; (2) – yes
(2) – yes; (1) – ?
(2) – no; (1) – yes
Logical Connective (Either or)
These statements are in the form of (either p or q). These are very simple statements. P and q are two statements. No cause and effect is present in this case.
Examples-
- I drink either green tea or juice.
- Either Ronak is intelligent or Raman is foolish.
In these type of statements clearly if one statement is false then second is true and if one is true second is false.
For ex.1
If I drink green tea it means surely I don’t drink juice. And If I drink juice it means surely I don’t drink green tea. No need to make cases here we can directly write conclusion.
Conclusion (Either, or)-
(1) – yes; (2) – no
(1) – no; (2) – yes
(2) – yes; (1) – no
(2) – no; (1) – yes
Note: In these type of statements clearly one of the statements is definitely true and one is definitely false.
Logical Connectives Summary Table

Tips to Solve Logical Connective Questions
- Rewrite any given statement such that the logical connective is at the beginning of the statement if it isn’t already.
- Reverse the conditions and see if the new statement is valid or not.
- Check to see if the negatives of both conditions still hold true.
- Practice as many questions as possible to know the variety of questions that are being asked.
Solved Examples
Q1: Based on the statement given below, identify which of the assumption/s is/are implicit:
Vikas says to Harry, "Refer to the Cambridge dictionary instead of Oxford dictionary to be good at English."
Assumption:
I. Harry wants to be good at English.
II. Vikas is a good advisor
(a)Only assumption I is implicit
(b)Only assumption II is implicit
(c)Both assumption I and II are implicit
(d)Neither assumption I nor II is implicit
Ans: Option A
Sol: Only assumption I is implicit. We cannot comment on assumption II.
Answer is option A.
Directions for Q2 to Q4:
Answer the following question based on the information given below.
Richie invites three of his friends Sunny, Pinky, and Nancy for his birthday party organized at his home. As the party goes on till late in the night, Sunny, Pinky, and Nancy choose to stay at Richie's house. Being good friends they usually stay back at each other's house. Each of them including Richie stay either in the room painted blue or in the painted purple. They have adequate number of rooms of both colours. The preferences which need to be fulfilled are:
1. If sunny stays in the room painted purple, then Pinky and Richie stay in the same room as Nancy.
2. If Pinky stays in the room painted purple, then Sunny stays in the room in which Nancy and Richie don't stay.
3. If Nancy stays in the room painted blue, then Sunny and Richie stay in the room which Pinky has chosen.
4. If Richie stays in the room painted Blue then Sunny and Pinky do not stay in the same room as Nancy.
Q2: Under all possible combinations which of the two friends will always have their room colours unchanged.
(a)Richie & Sunny
(b)Pinky & Richie
(c)Nancy & Sunny
(d)Nancy & Pinky
Ans: Option C
Sol: The following table can be made using the given 4 conditions :
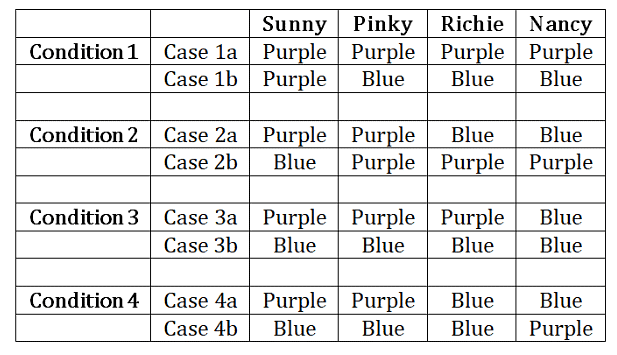
Case 2a, 3a and 4a violates condition I, so these 3 cases are invalid.
Case 1a, 1b violates condition iii, so these cases are invalid.
Case 3b violates condition iv, so this case is invalid.
Finally we have the following two cases:
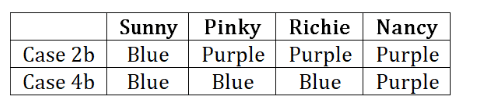
Q3: If Richie chose to stay in the room painted blue, then in which room does Pinky stay?
(a)Purple
(b)Blue
(c)Data Inadequate
(d)None of the above
Ans: Option A
Sol:The following table can be made using the given 4 conditions :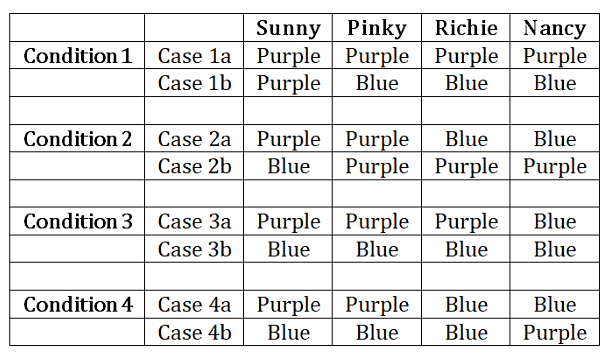
Case 2a, 3a and 4a violate condition I, so these 3 cases are invalid.
Case 1a, 1b violate condition iii, so these cases are invalid.
Case 3b violates condition iv, so this case is invalid.
Finally we have the following two cases: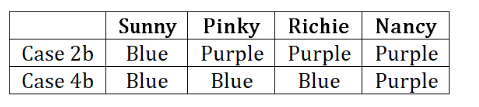
Purple
Q4: If Pinky does not like to stay in the blue painted room, then where will Sunny stay
(a)Blue
(b)Purple
(c)Data Inadequate
(d)None of the above
Ans: Option A
Sol: The following table can be made using the given 4 conditions :
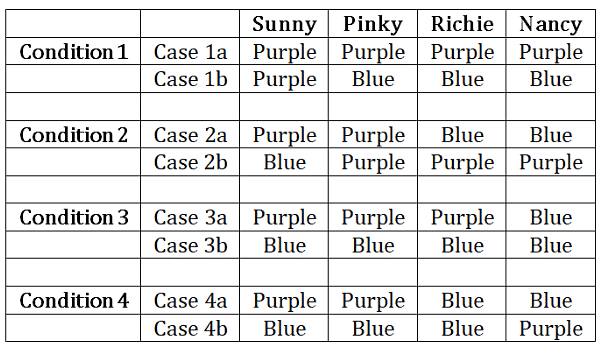
Case 2a, 3a and 4a violates condition I, so these 3 cases are invalid.
Case 1a, 1b violates condition iii, so these cases are invalid.
Case 3b violates condition iv, so this case is invalid.
Finally we have the following two cases:
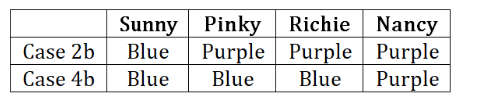
Blue
Hence, option (a).
Q5: Based on the given statement, choose the right conclusion:
‘If the breakfast doesn’t have eggs, I will not go for a walk and will not have lunch.’
(a)If I went for a walk and didn’t have lunch, the breakfast didn’t have eggs.
(b)If I went for a walk or I had lunch, the breakfast had eggs.
(c)If I went for a walk or I had no lunch, the breakfast had eggs.
(d)If I didn’t go for a walk and had lunch, the breakfast had eggs.
Ans: Option B
Sol: Let,A = The breakfast doesn't have eggs
B = I will not go for a walk and will not have lunch.
From the logical deductions,
AB = ~B~A
Also, and is replaced by or and vice versa.So,
~A = The breakfast has eggs.
~B = I will go for a walk or will have lunch.
So, we get,
~B~A = I will go for a walk or will have lunch, the breakfast has eggs.
Hence, option (b).
Q6: Find the statement which is necessarily true according to the given information:The Asatra Vriksh is an evergreen tree that grows in the Nilgiris. The Asatra Vriksh has a fleshy, poisonous fruit. Recently, Purol, a substance found in the bark of the Asatra Vriksh, was discovered to be a promising new antidepressant drug.
(a)Purol is poisonous when taken by healthy people.
(b)Purol has cured people from various diseases.
(c)People should not eat the fruit of Asatra Vriksh.
(d)No treatment for depression was known till Purol was discovered.
Ans: Option C
Sol: Option 1 is incorrect as the passage clearly mentions that the fruit of the tree is poisonous not Purol.
According to the passage, Purol only has anti-depressant properties. This eliminates option 2.
According to the passage, Purol is a “promising new drug”. This indicates that drugs treating depression existed prior to the discovery of Purol. This eliminates option 4.
Option 3 is necessarily true as according to the passage, “The Asatra Vriksha has a fleshy, poisonous fruit”.
Hence, the correct answer is option 3.
Q7: ABCDE play a game of cards. ‘A’ tells ‘B’ that if ‘B’ gives him five cards ‘A’ will have as many cards as ‘E’ has. However if A gives five cards to ‘B’ then ‘B’ will have as many cards as ‘D’. A and B together has 20 cards more than what D and E have together. B has four cards more than what C has and total number of cards are 201. How many cards B have?
(a)185
(b)37
(c)175
(d)27
Ans: Option A
Sol: Data given in the question is not correct.
Let a, b, c, d and e be the number of cards with A, B, C, D and E.
If B gives A five cards, A will have as many cards as E.∴ e = a + 5 …(I)
If A gives B five cards, B will have as many cards as D.∴ d = b + 5 …(ii)
A and B together have 20 cards more than what D and E have together.∴ a + b = e + d + 20 …(iii)
It is also given that B has four cards more than what C has and the total number of cards are 201.
∴ b = c + 4 and …(iv)
a + b + c + d + e = 201 …(v)
Adding (i) and (ii) we get e + d = a + b + 10 which contradicts equation (iii)
∴ The data given in the question is not correct.
Q8: A research study recorded that the number of unemployed educated youth was equal to the number of unemployed uneducated youth. It was concluded by the researchers that being educated does not enhance the probability of being employed.Which of the following information would be required to validate the above conclusion?
(a)The number unemployed educated and uneducated people in other age groups.
(b)The number of organisations employing youth.
(c)The percentage of unemployment in educated youth versus percentage of unemployment in uneducated youth.
(d)The percentage increase in number of educated youth versus last year.
Ans: Option C
Sol: The passage is a comparison between the raw data resulting from a study. There were as many unemployed educated youth as unemployed uneducated youth. The conclusion being that education provided no guarantee in securing employment.
Option 1 is incorrect because these numbers are not really comparable as this data would not be able to either support or disqualify the findings of the study as option 1 does not pertain to youths.
Option 2 is incorrect as just this information would not suffice to prove the study findings.
Option 4 is incorrect because it only considers the increased number of educated youth. This is not complete information to support the study findings.
Option 3 is correct because the percentage figures would provide comparative data to validate the conclusion mentioned in the passage.
Hence, the correct answer is option 3.
|
193 videos|169 docs|152 tests
|
FAQs on CAT Logical Connectives : Basic Concepts and Notes PDF
| 1. What are Logical Connectives and why are they important in solving questions related to topics like If, then, only if/when, If and Only If, unless, and Either or? |  |
| 2. How can one effectively solve questions involving Logical Connectives like If, then, only if/when, If and Only If, unless, and Either or? |  |
| 3. Can you provide an example of a question that involves the Logical Connective "If and Only If" and how to solve it? |  |
| 4. How can one differentiate between the Logical Connectives "unless" and "Either or" in solving logical reasoning questions? |  |
| 5. What are some tips to effectively solve Logical Connective questions in exams like CAT? |  |

















