Introduction: Trigonometric Ratios | Mathematics (Maths) Class 10 PDF Download
Introduction to Trigonometric Ratios of a Triangle
Trigonometry is all about triangles or to be more precise about the relation between the angles and sides of a right-angled triangle. There are three sides of a triangles named as Hypotenuse, Adjacent, and Opposite. The ratio between these sides based on the angle between them are called Trigonometric Ratios.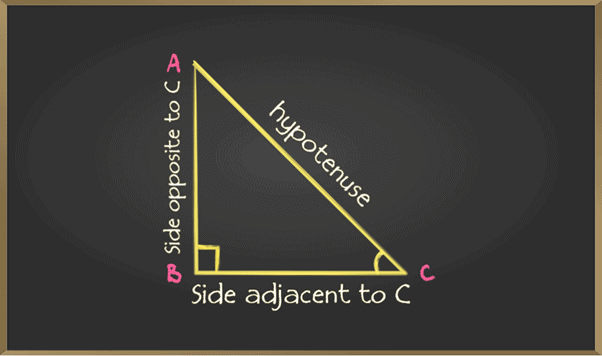
As given in the figure in a right-angle triangle
- The side opposite to the right angle is called the hypotenuse
- The side opposite to an angle is called the opposite side
(i) For angle C opposite side is AB
(ii) For angle A opposite side is BC - The side adjacent to an angle is called the adjacent side
(i) For angle C adjacent side is BC
(ii) For angle A adjacent side is AB
Trigonometric ratios
There are 6 basic trigonometric relations that form the basics of trigonometry. These 6 trigonometric relations are ratios of all the different possible combinations in a right-angled triangle.
These trigonometric ratios are called
- Sine
- Cosine
- Tangent
- Cosecant
- Secant
- Cotangent
The mathematical symbol θ is used to denote the angle.
A. Sine (sin)
Sine of an angle is defined by the ratio of lengths of sides which is opposite to the angle and the hypotenuse. It is represented as sinθ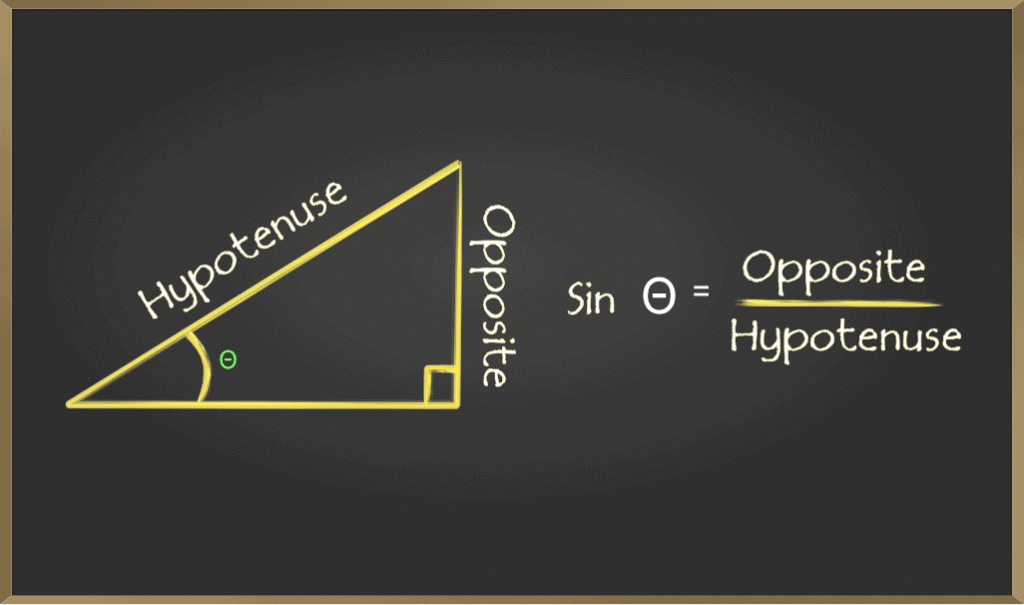
B. Cosine (cos)
Cosine of an angle is defined by the ratio of lengths of sides which is adjacent to the angle and the hypotenuse. It is represented as cosθ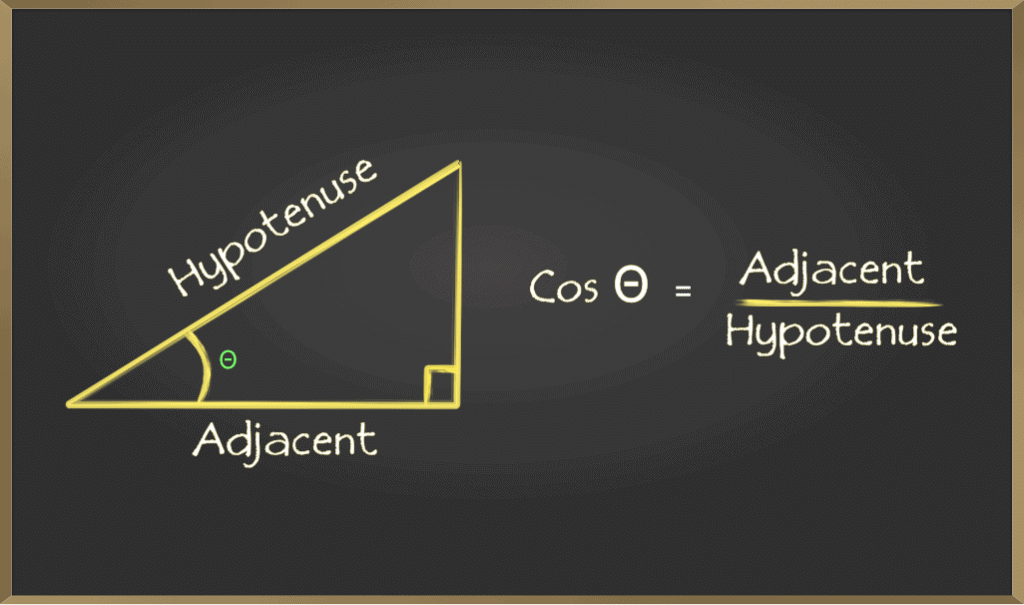 C. Tangent (tan)
C. Tangent (tan)
Tangent of an angle is defined by the ratio of length of sides which is opposite to the angle and the side which is adjacent to the angle. It is represented as tanθ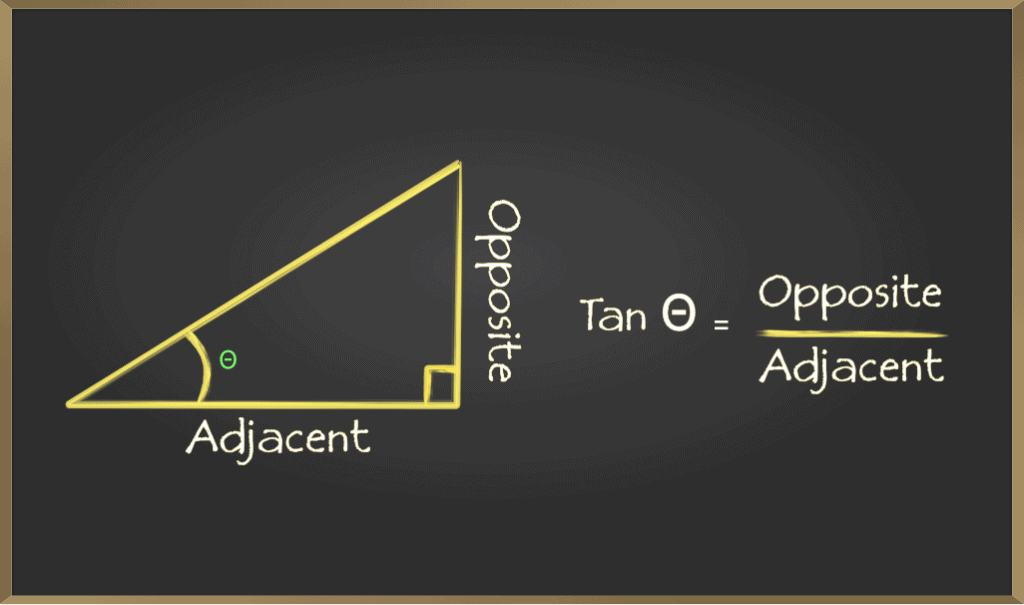 D. Cosecant (csc)
D. Cosecant (csc)
Cosecant of an angle is defined by the ratio of length of the hypotenuse and the side opposite the angle. It is represented as cscθ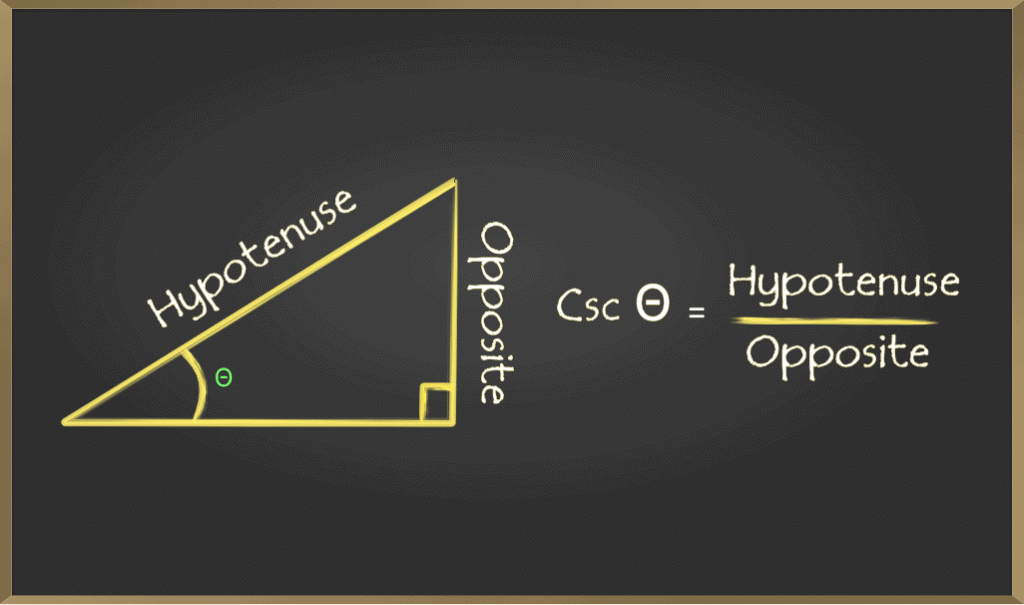 E. Secant(sec)
E. Secant(sec)
Secant of an angle is defined by the ratio of length of the hypotenuse and the side and the side adjacent to the angle. It is represented as secθ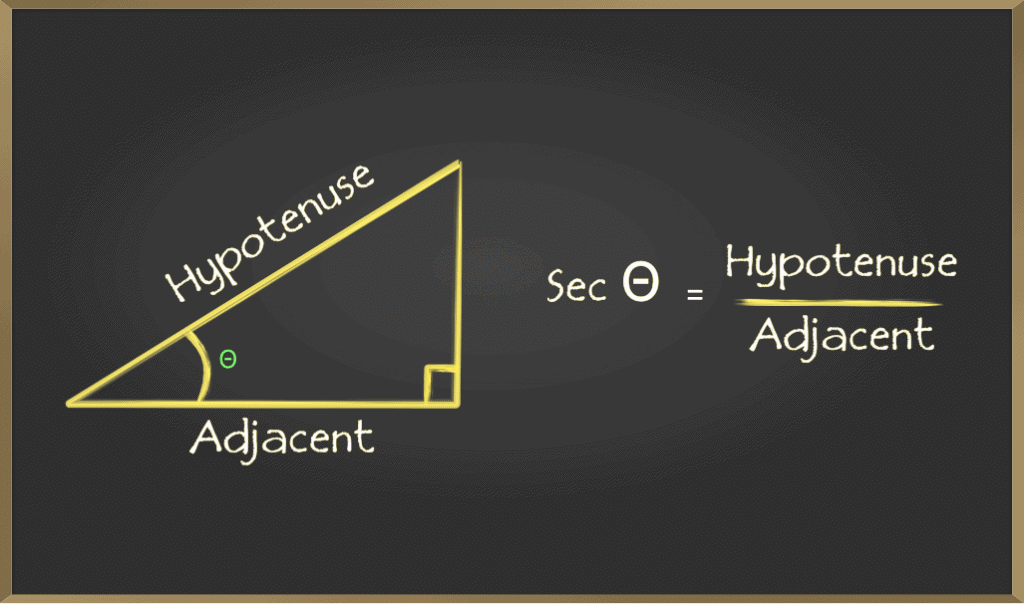 F. Cotangent(cot)
F. Cotangent(cot)
Cotangent of an angle is defined by the ratio of length of sides which is adjacent to the angle and the side which is opposite to the angle. It is represented as cotθ.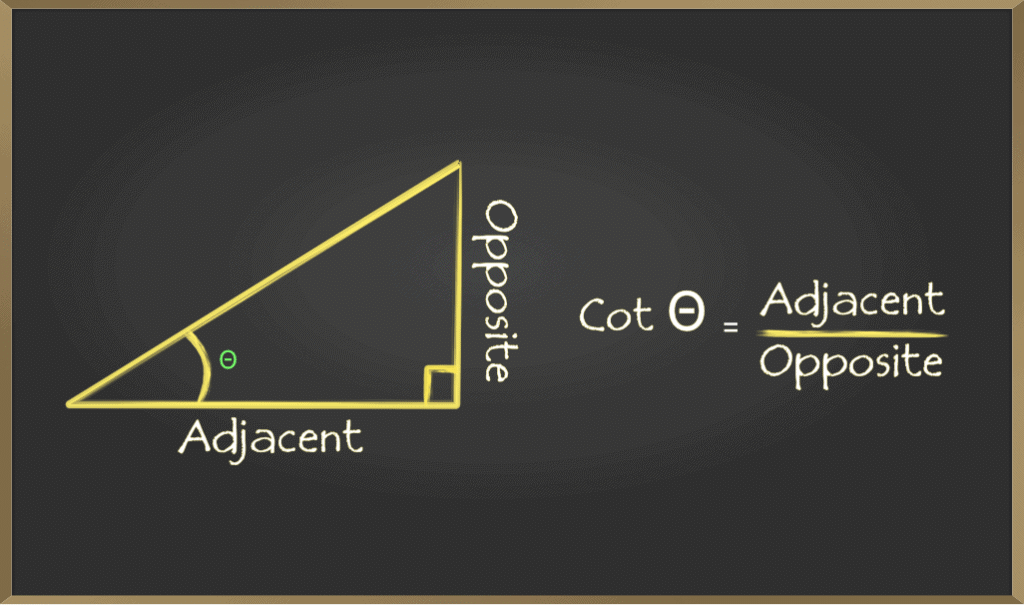
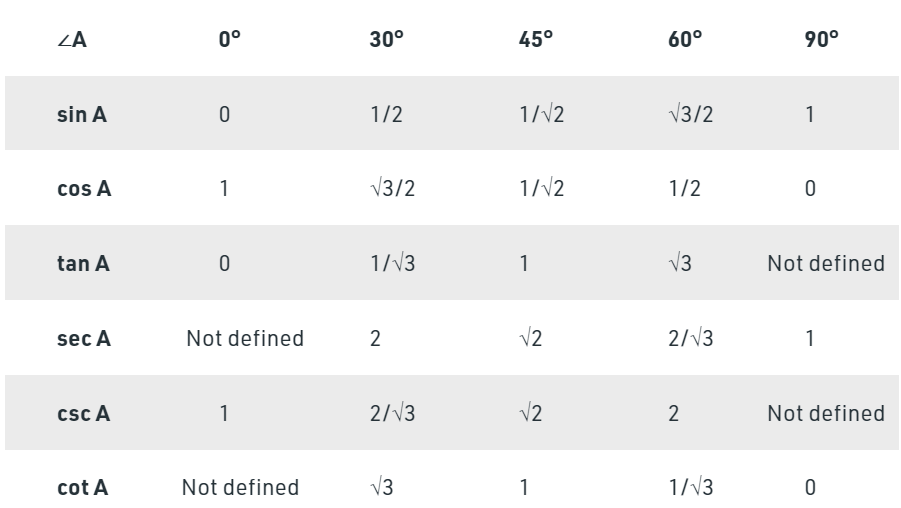
Trigonometric table
Trigonometric Ratio | Abbreviation | Formula |
sine | sin | Opposite/Hypotenuse |
cosine | cos | Adjacent/Hypotenuse |
tangent | tan | Opposite/Adjacent |
cosecant | csc | Hypotenuse/Opposite |
secant | sec | Hypotenuse/Adjacent |
cotangent | cot | Adjacent/Opposite |
Solving for a side in right triangles with trigonometry
This is one of the most basic and useful use of trigonometry using the trigonometric ratios mentioned is to find the length of a side of a right-angled triangle but to do, so we must already know the length of the other two sides or an angle and length of one side.
Steps to follow if one side and one angle are known:
- Choose a trigonometric ratio which contains the given side and the unknown side
- Use algebra to find the unknown side
Example: In a right angled ΔABC ∠B — 30 length of side A B is 4 find length of BC. given tan30 = 1/√3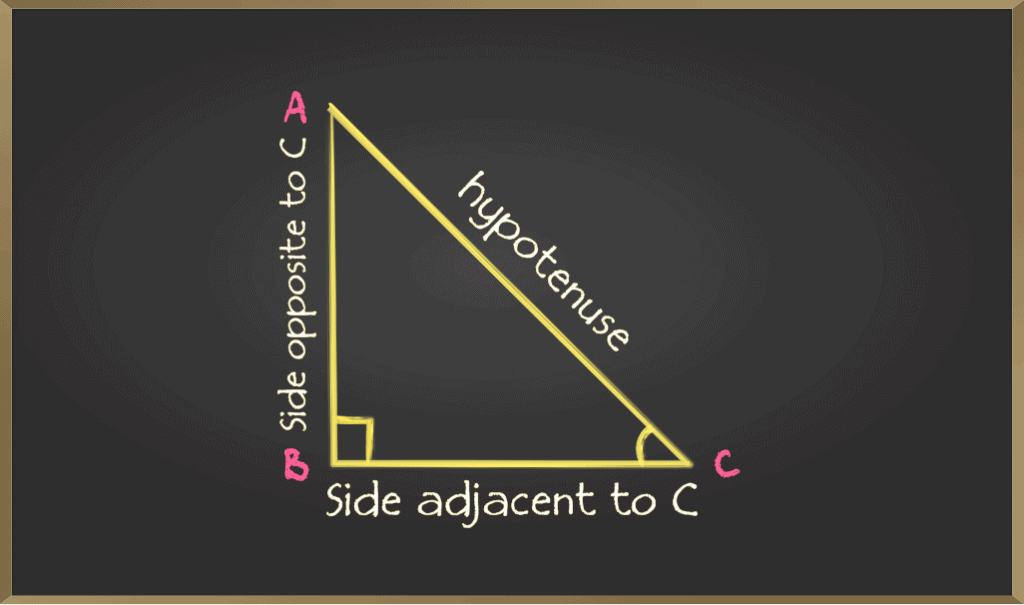 Solution:
Solution: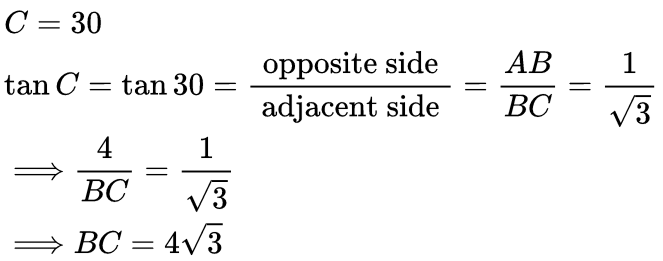
Steps to follow if two sides are known:
- Mark the known sides as adjacent, opposite or hypotenuse with respective to anyone of the acute angles in the triangle.
- Decide on which trigonometric ratio can be found out from the above table.
- Find the angle (X)
- Use an trigonometric ratio with respect to X which is a ratio of a known side and an unknown side.
- Use algebra to find the unknown side.
Trigonometric Ratios of Some Specific Angles
Trigonometry is all about triangles or to more precise about the relation between the angles and sides of a right-angled triangle. In this article we will be discussing about the ratio of sides of a right-angled triangle respect to its acute angle called trigonometric ratios of the angle and find the trigonometric ratios of specific angles: 0°, 30°, 45°, 60°, and 90°.
Consider the following triangle: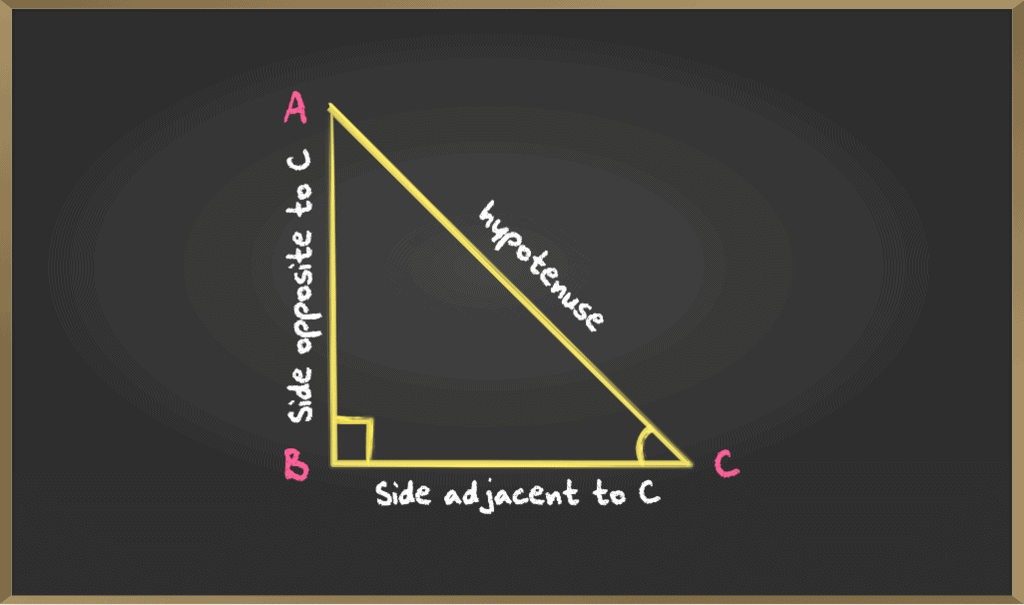
The side BA is opposite to angle ∠BCA so we call BA the opposite side to ∠C and AC is the hypotenuse, the other side BC is the adjacent side to ∠C.
Trigonometric Ratios of angle C
Sine: Sine of ∠C is the ratio between BA and AC that is the ratio between the side opposite to C and the hypotenuse.
Sin C = BA/AC
Cosine: Cosine of ∠C is the ratio between BC and AC that is the ratio between the side adjacent to C and the hypotenuse.
Cos C = BC/AC
Tangent: Tangent of ∠C is the ratio between BA and BC that is the ratio between the side opposite and adjacent to C
Tan C = BA/BC
Cosecant: Cosecant of ∠C is the reciprocal of sin C that is the ratio between the hypotenuse and the side opposite to C.
csc C = BA/AC
Secant: Secant of ∠C is the reciprocal of cos C that is the ratio between the hypotenuse and the side adjacent to C.
sec C = BA/AC
Cotangent: Cotangent of ∠C is the reciprocal of tan C that is the ratio between the side adjacent to C and side opposite to C.
Cot C = BA/AC
Finding trigonometric ratios for angle 0°, 30°, 45°, 60°, 90°
A. For angles 0° and 90°
If an angle A = 0° then the length of the opposite side would be zero and hypotenuse = adjacent side and if A = 90° then the hypotenuse = opposite side. So by using the above formulas for the trigonometric ratios and if the length of the hypotenuse is a.
if A = 0°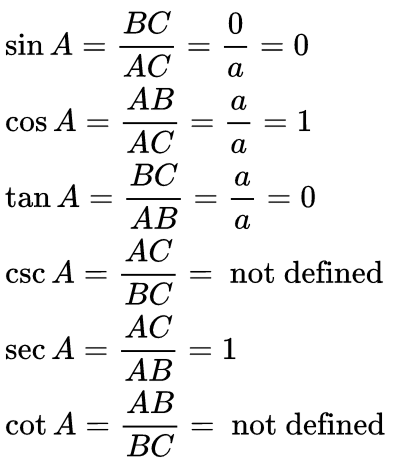 if A = 90°
if A = 90°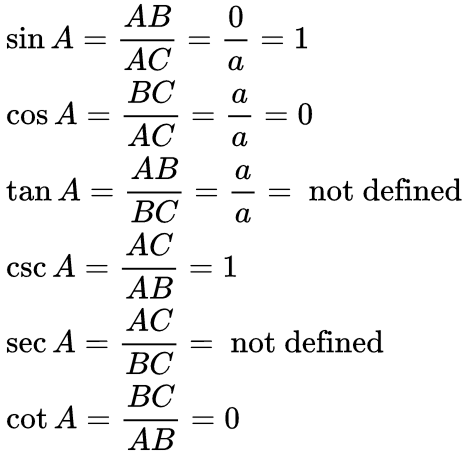 Here cosec 0, cot 0, tan 90 and sec 90 are not defined as at the particular angle it is divided by 0 which is undefined.
Here cosec 0, cot 0, tan 90 and sec 90 are not defined as at the particular angle it is divided by 0 which is undefined.
B. For angles 30° and 60°
Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore, ∠A = ∠B = ∠C = 60°.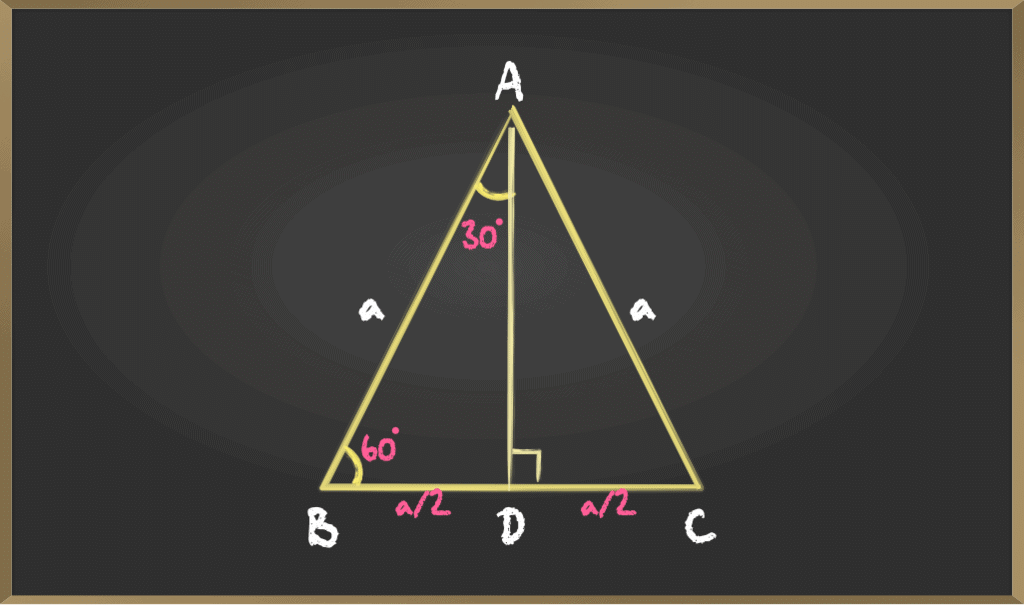 ∆ABD is a right triangle, right-angled at D with ∠BAD = 30° and ∠ABD = 60°, Here ∆ADB and ∆ADC are similar as they are Corresponding parts of Congruent triangles(CPCT).
∆ABD is a right triangle, right-angled at D with ∠BAD = 30° and ∠ABD = 60°, Here ∆ADB and ∆ADC are similar as they are Corresponding parts of Congruent triangles(CPCT).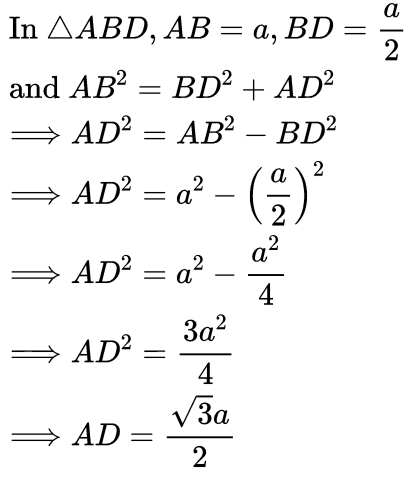 Now we know the values of AB, BD, and AD, So the trigonometric ratios for angle 30 are
Now we know the values of AB, BD, and AD, So the trigonometric ratios for angle 30 are For angle 60°
For angle 60°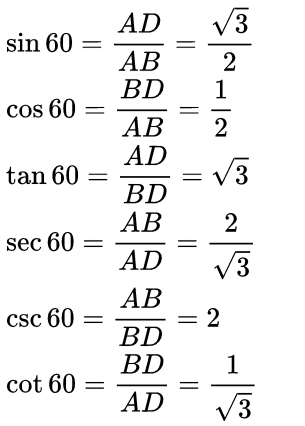 C. For angle 45°
C. For angle 45°
In a right-angled triangle if one angle is 45° then the other angle is also 45° thus making it an isosceles right angle triangle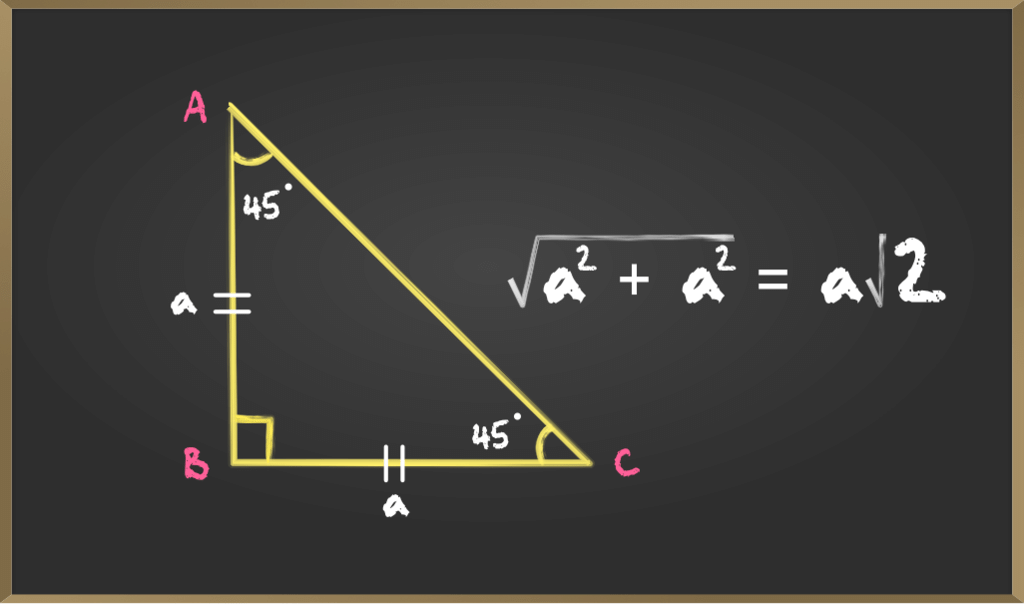 If the length of side BC = a then length of AB = a and Length of AC(hypotenuse) is a√2, then
If the length of side BC = a then length of AB = a and Length of AC(hypotenuse) is a√2, then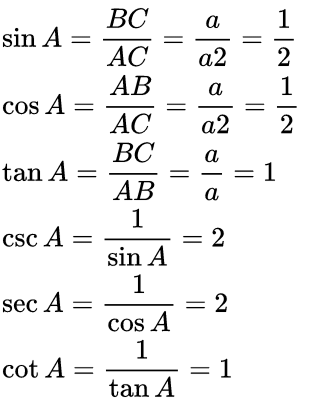 Result
Result
Trigonometric Identities
An equation involving trigonometric ratios of an angle is called trigonometric Identity if it is true for all values of the angle. These are useful whenever trigonometric functions are involved in an expression or an equation. The six basic trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. All these trigonometric ratios are defined using the sides of the right triangle, such as an adjacent side, opposite side, and hypotenuse side.
Proof of the Trigonometric Identities
For any acute angle θ, prove that
(i) tanθ = sinθ/cosθ
(ii) cotθ = cosθ/sinθ
(iii) tanθ . cotθ = 1
(iv) sin2θ + cos2θ = 1
(v) 1 + tan2θ = sec2θ
(vi) 1 + cot2θ = cosec2θ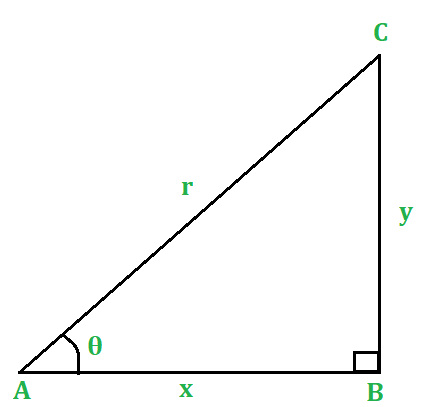
Proof:
Consider a right-angled △ABC (fig. 1) in which ∠B = 90° and ∠A = 0°.
Let AB = x units, BC y units and AC = r units.
Then,
(i) tanθ = y/x = (y/r)/(x/r) [dividing num. and denom. by r]
∴ tanθ = sinθ/cosθ
(ii) cotθ = x/y = (x/r)/(y/r) [dividing num. and denom. by r]
∴ cotθ = cosθ/sinθ
(iii) tanθ . cotθ = (sinθ/cosθ) . (cosθ/sinθ)
tanθ . cotθ = 1
Then, by Pythagoras’ theorem, we have
x2 + y2 = r2.
Now,
(iv) sin2θ + cos2θ = (y/r)2 + (x/r)2 = ( y2/r2 + x2/r2)
= (x2 + y2)/r2 = r2/r2 = 1 [x2+ y2 = r2]
sin2θ + cos2θ = 1
(v) 1 + tan2θ = 1 + (y/x)2 = 1 + y2/x2 = (y2 + x2)/x2 = r2/x2 [x2 + y2 = r2]
(r/x)2 = sec2θ
∴ 1 + tan2θ = sec2θ.
(vi) 1 + cot2θ = 1 + (x/y)2 = 1 + x2/y2 = (x2 + y2)/y2 = r2/y2 [x2 + y2 = r2]
(r2/y2) = cosec2θ
∴ 1 + cot2θ = cosec2θ.
Application of Trigonometric Identites
Application 1: Prove that (1 – sin2θ) sec2θ = 1
Proof:
We have:
LHS = (1 – sin2θ) sec2θ
= cos2θ . sec2θ
= cos2θ . (1/cos2θ)
=1
= RHS.
∴ LHS = RHS.
Application 2: Prove that (1 + tan2θ) cos2θ = 1
Proof:
We have:
LHS = (1 + tan2θ)cos2θ
= sec2θ . cos2θ
= (1/cos2θ) . cos2θ
= 1 = RHS.
∴ LHS=RHS.
Application 3: Prove that (cosec2θ – 1) tan²θ = 1
Proof:
We have:
LHS = (cosec²θ – 1) tan2θ
= (1 + cot2θ – 1) tan2θ
= cot2θ . tan2θ
= (1/tan2θ) . tan2θ
= 1 = RHS.
∴ LHS=RHS.
Application 4: Prove that (sec4θ – sec2θ) = (tan2θ + tan4θ)
Proof:
We have:
LHS = (sec4θ – sec2θ)
= sec2θ(sec2θ – 1)
= (1 + tan2θ) (1 + tan2θ – 1)
= (1 + tan2θ) tan2θ
= (tan2θ + tan4θ)
= RHS
∴ LHS = RHS.
Application 5: Prove that √(sec2θ + cosec2θ) = (tanθ + cotθ)
Proof:
We have:
LHS = √(sec2θ + cosec2θ ) = √((1 + tan2θ) + (1 + cot2θ))
= √(tan2θ + cot2θ + 2)
= √(tan2θ + cot2θ + 2tanθ.cotθ ) (tanθ . cotθ = 1)
= √(tanθ + cotθ)2
= tanθ + cotθ = RHS
∴ LHS = RHS.
|
127 videos|584 docs|79 tests
|
FAQs on Introduction: Trigonometric Ratios - Mathematics (Maths) Class 10
| 1. What are the basic trigonometric ratios and how are they defined in a right triangle? |  |
| 2. What are the trigonometric ratios for the angles 30°, 45°, and 60°? |  |
| 3. How can trigonometric identities be useful in solving problems? |  |
| 4. What are some common trigonometric identities to remember? |  |
| 5. How do you find the values of trigonometric ratios using a right triangle? |  |
















