Introduction to Binomial Theorem | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| Need for Binomial Theorem |

|
| Pascal’s Triangle |

|
| Binomial theorem for any positive integer n |

|
| Solved Examples on Binomial Theorem |

|
Need for Binomial Theorem
- From our knowledge so far, we've mastered finding the squares and cubes of binomials, like unwrapping the secrets hidden within expressions such as (a + b)² and (a – b)³. These skills allowed us to effortlessly compute values like (98)² or (999)³. But, as we venture into higher powers, like (98)⁵ or (101)⁶, the path becomes strewn with the complexity of repeated multiplication.
- To solve this problem, the binomial theorem was introduced! This theorem provides us with a magical formula to effortlessly expand expressions like (a + b)n, where 'n' can be any integer or even a rational number.

- Let's revisit a few identities to study the binomial theorem:
(a + b)0 = 1 (assuming a + b ≠ 0)
(a+b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = (a + b)3 · (a + b) = a4 + 4a3 b + 6a2b2 + 4ab3 + b4
As we examine these expansions, a few patterns emerge:
- The total number of terms in the expansion is consistently one more than the index. For instance, when expanding (a+b)2, we find 3 terms, aligning with the index 2.
- Notice the difference between the powers of 'a' and 'b' in each term. The power of 'a' decreases by 1 with each successive term, while the power of 'b' increases by 1.
- Dive a bit deeper into the structure of each term, and you'll discover a harmonious relationship: the sum of the indices of 'a' and 'b' in every term equals the overall index of a+b. It's like a mathematical symphony where each note plays a crucial role in composing the whole.
So, what's the story behind these patterns? Let's unravel the mysteries together as we explore the underlying principles of these binomial expansions.
Pascal’s Triangle
- Pascal's Triangle is a triangular representation of numbers where each number is the sum of the two numbers directly above it. It has numerous applications in combinatorics and is particularly useful in understanding and expanding binomial expressions.
- Each row in Pascal's Triangle corresponds to the coefficients of the binomial expansion of (a+b)n,
where n is the row number (starting with the zeroth row). - Let's illustrate this concept by drawing Pascal's Triangle for the first few rows:
 Pascal's Triangle
Pascal's Triangle - Now, let's say we want to expand (a+b)4
We can use the coefficients from the fourth row of Pascal's Triangle:
(a + b)4 =1a4 + 4a3b + 6a2b2 + 4 ab3 + 1b4 - So, the coefficients are 1, 4, 6, 4, 1, which correspond to the fourth row of Pascal's Triangle. Notice how these coefficients match the numbers in the fifth row of the triangle.
- Pascal's Triangle provides a convenient way to determine the coefficients of the binomial expansion without having to perform lengthy calculations.
- Keep in mind that the first row of Pascal's Triangle corresponds to
(a+b)0 = 1, and each subsequent row corresponds to the expansion of
(a+b)n where n is the row number.
Binomial theorem for any positive integer n
According to the binomial theorem, it is possible to expand any non-negative power of binomial (x + y) into a sum of the form
 Binomial Theorem
Binomial Theorem
Binomial Theorem Representation
The binomial theorem is expressed using the sigma notation
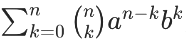 Where,
Where,  represents the binomial coefficient, and a and b are constants. This formula expands (a+b)n and is a shorthand way of writing out the terms.
represents the binomial coefficient, and a and b are constants. This formula expands (a+b)n and is a shorthand way of writing out the terms.
Binomial Coefficients
The coefficients  in the binomial theorem are known as binomial coefficients. These coefficients represent the number of ways to choose k elements from a set of n elements.
in the binomial theorem are known as binomial coefficients. These coefficients represent the number of ways to choose k elements from a set of n elements.
Number of Terms
The expansion of (a+b)n has n+1 terms, which is one more than the index n. Each term corresponds to a specific power of a and b in the binomial expression.
Decreasing Powers of a and Increasing Powers of b
- In the successive terms of the expansion, the power (index) of a decreases by 1, starting with n and ending with 0.
- Simultaneously, the power of b increases by 1, starting with 0 and ending with n.
Sum of Indices
- The sum of the indices of a and b in each term is always equal to the index n. This means that in every term of the expansion, a and b together have a total exponent of n.
- The binomial theorem provides a systematic way to expand expressions of the form (a+b)n by distributing the powers and coefficients according to these observations, making complex calculations more manageable.
Solved Examples on Binomial Theorem
Example 1: Expand (x+y)3 using binomial theorem
Solution: The binomial theorem formula for this expansion is:
Now, let's calculate each term: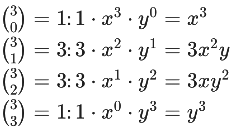
Now, combine these terms
(x + y)3 = x3 + 3x2y + 3xy2 + y3
This is the expanded form of (x+y)3
Each term represents a unique combination of powers of x and y, and the coefficients 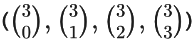 come from Pascal's Triangle.
come from Pascal's Triangle.
We can use a similar approach for higher powers or different binomial expressions. The binomial theorem provides a systematic way to expand such expressions without going through the cumbersome process of repeated multiplication.
Example 2: Expand (x2 + 2)6
Solution:
(x2 +2)6 = 6C0 (x2)6(2)0 + 6C1(x2)5(2)1 + 6C2(x2)4(2)2 + 6C3 (x2)3(2)3 + 6C4 (x2)2(2)4 + 6C5 (x2)1(2)5 + 6C6 (x2)0(2)6
= (1) (x12) (1) + (6) (x10) (2) + (15) (x8) (4) + (20) (x6) (8) + (15) (x4) (16) + (6) (x2) (32) + (1)(1) (64)
= x12 + 12 x10 + 60 x8 + 160 x6 + 240 x4 + 192 x2 + 64
Example 3: Expand the expression (√2 + 1)5 + (√2 − 1)5 using the Binomial formula.
Solution:
(x + y)5 + (x – y)5 = 2[5C0 x5 + 5C2 x3 y2 + 5C4 xy4]
= 2(x5 + 10 x3 y2 + 5xy4)
= (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2) (1)4]
=58√2
|
172 videos|503 docs|154 tests
|
FAQs on Introduction to Binomial Theorem - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the significance of the Binomial Theorem in mathematics? |  |
| 2. How is Pascal’s Triangle related to the Binomial Theorem? |  |
| 3. Can the Binomial Theorem be applied to any positive integer value of n? |  |
| 4. Can you provide an example of how the Binomial Theorem is used in solving mathematical problems? |  |
| 5. What is the importance of understanding the Binomial Theorem for students preparing for exams like JEE? |  |















