Introduction to Determinants | Mathematics (Maths) for JEE Main & Advanced PDF Download

Having studied about Matrices; welcome to a new chapter in your syllabus– Determinants. In this chapter, we'll explore a fundamental concept that holds significant importance in linear algebra. Determinants are mathematical tools that help us understand the properties of matrices and the transformations they represent.

Think of determinants as a numerical signature of a matrix, revealing crucial information about its behavior. From solving systems of linear equations to understanding geometric transformations, determinants play a pivotal role in various mathematical applications.

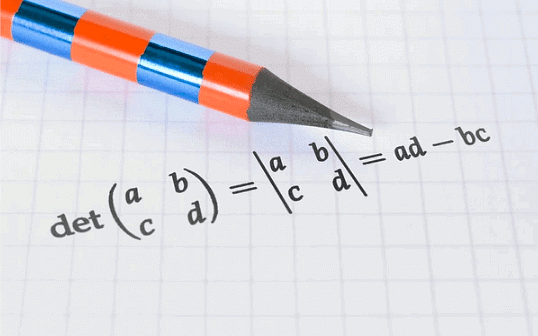
So, as we delve into this chapter, you'll discover the practical significance of determinants and how they contribute to solving real-world mathematical problems.

How do we write a Determinant?

In linear algebra, every square matrix

A=[a_ij] of order n is associated with a singular number, known as the determinant. This determinant is denoted by ∣A∣, detA, or Δ, can be a real or complex number. It serves as a unique function that maps each square matrix to a specific numerical value.

To elaborate, consider a function f that operates on the set of square matrices M and produces results in the set of numbers K, whether real or complex. This function is defined as f(A)=k, where A belongs to M and k belongs to K. In simpler terms, f(A) is precisely what we refer to as the determinant of matrix A.

For example, let's take a 2x2 matrix: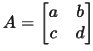

The determinant of A, denoted as ∣A∣, is calculated as: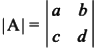

∣A∣=a⋅d−b⋅c

In this way, determinants encapsulate essential information about the matrix, reflecting its unique characteristics. They find extensive applications in solving systems of linear equations, analyzing transformations, and understanding the inherent properties of square matrices. 

Note:
(i) For matrix A, |A| is read as the determinant of A and not modulus of A.
(ii) Only square matrices have determinants.

And what about a determinant with order 1?

i.e A = [a] be the matrix of order 1, then determinant of A is defined to be equal to a

Solved Example:

Calculate the determinant for the given matrix:

let's calculate the determinant (∣A∣) using the formula for a 2x2 matrix:
∣A∣=(3⋅2)−(4⋅1)
∣A∣=6−4
∣A∣=2
So, for the given matrix A, the determinant ∣A∣ is 2.

Determinant of a matrix of order 3 × 3

Consider the determinant of a 3 × 3 matrix is written as
det A =

The value of the determinant can be found out by expansion of the matrix along any row.
det A=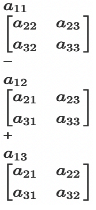

Lets see an example to help understand better.

Example: For the given 3x3 matrix, calculate its determinant by expansion along the first row.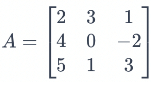

Calculate the determinant (∣A∣) by expanding along the first row:

Now, calculate the determinants of the 2x2 matrices:
∣A∣=2⋅(0⋅3−(−2)⋅1)−3⋅(4⋅3−(−2)⋅5)+1⋅(4⋅1−0⋅5)
∣A∣=2⋅(0+2)−3⋅(12+10)+1⋅4
∣A∣=4−66+4
∣A∣=−58

Similarly, we can expand the big determinant along any row or any column and break it down into smaller determinants to get your answer.

Area of a Triangle

Area of a triangle formed by three vertices(x₁, y₁), (x₂, y₂), and (x₃, y₃) in the Cartesian plane can be calculated using determinants. The formula for the area (A) is given by:

This formula is derived from the fact that the area of a triangle formed by three points in the Cartesian plane is half the absolute value of the determinant of a 3x3 matrix formed by the coordinates of the vertices and an additional column of ones.
Let's illustrate this with an example:
Example: Find the area of the triangle with vertices (1,2), (3,4), and (5,1) (5,1).
The area (A) can be calculated as follows: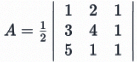

Now, compute the determinant: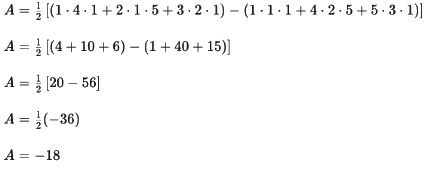

So, the area of the triangle formed by the given vertices is 18 square units. Note that the absolute value of the determinant is taken to ensure the area is non-negative.