Introduction to Turbulent Flow - 1 | Fluid Mechanics for Mechanical Engineering PDF Download
| Table of contents |

|
| Introduction |

|
| Characteristics Of Turbulent Flow |

|
| Laminar-Turbulent Transition |

|
| Correlation Functions |

|
Introduction
- The turbulent motion is an irregular motion.
- Turbulent fluid motion can be considered as an irregular condition of flow in which various quantities (such as velocity components and pressure) show a random variation with time and space in such a way that the statistical average of those quantities can be quantitatively expressed.
- It is postulated that the fluctuations inherently come from disturbances (such as roughness of a solid surface) and they may be either dampened out due to viscous damping or may grow by drawing energy from the free stream.
- At a Reynolds number less than the critical, the kinetic energy of flow is not enough to sustain the random fluctuations against the viscous damping and in such cases laminar flow continues to exist.
- At somewhat higher Reynolds number than the critical Reynolds number, the kinetic energy of flow supports the growth of fluctuations and transition to turbulence takes place.
Characteristics Of Turbulent Flow
- The most important characteristic of turbulent motion is the fact that velocity and pressure at a point fluctuate with time in a random manner.
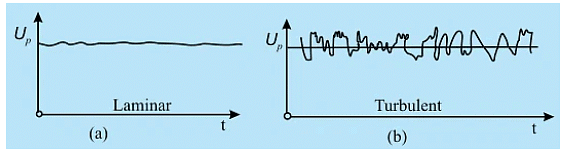
Fig. 32.1 Variation of horizontal components of velocity for laminar and turbulent flows at a point P
- The mixing in turbulent flow is more due to these fluctuations. As a result we can see more uniform velocity distributions in turbulent pipe flows as compared to the laminar flows .
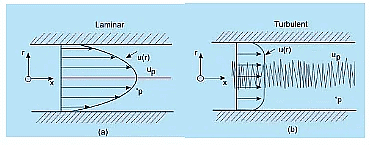
Fig. 32.2 Comparison of velocity profiles in a pipe for (a) laminar and (b) turbulent flows of layers of fluids with different velocities over one another
Turbulence can be generated by frictional forces at the confining solid walls. The turbulence generated in these two ways are considered to be different. Turbulence generated and continuously affected by fixed walls is designated as wall turbulence , and turbulence generated by two adjacent layers of fluid in absence of walls is termed as free turbulence. One of the effects of viscosity on turbulence is to make the flow more homogeneous and less dependent on direction.
Turbulence can be categorised as below:
1.Homogeneous Turbulence: Turbulence has the same structure quantitatively in all parts of the flow field.
2.Isotropic Turbulence: The statistical features have no directional preference and perfect disorder persists.
3.Anisotropic Turbulence: The statistical features have directional preference and the mean velocity has a gradient.
1.Homogeneous Turbulence : The term homogeneous turbulence implies that the velocity fluctuations in the system are random but the average turbulent characteristics are independent of the position in the fluid, i.e., invariant to axis translation.
Consider the root mean square velocity fluctuations
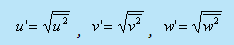
In homogeneous turbulence, the rms values of u', v' and w' can all be different, but each value must be constant over the entire turbulent field. Note that even if the rms fluctuation of any component, say u' s are constant over the entire field the instantaneous values of u necessarily differ from point to point at any instant.
2. Isotropic Turbulence: The velocity fluctuations are independent of the axis of reference, i.e. invariant to axis rotation and reflection. Isotropic turbulence is by its definition always homogeneous. In such a situation, the gradient of the mean velocity does not exist, the mean velocity is either zero or constant throughout.
- In isotropic turbulence fluctuations are independent of the direction of reference and
it is re-emphasised that even if the rms fluctuations at any point are same, their instantaneous values necessarily differ from each other at any instant.
- Turbulent flow is diffusive and dissipative . In general, turbulence brings about better mixing of a fluid and produces an additional diffusive effect. Such a diffusion is termed as "Eddy-diffusion ".( Note that this is different from molecular diffusion)
- At a large Reynolds number there exists a continuous transport of energy from the free stream to the large eddies. Then, from the large eddies smaller eddies are continuously formed. Near the wall smallest eddies destroy themselves in dissipating energy, i.e., converting kinetic energy of the eddies into intermolecular energy.
Laminar-Turbulent Transition
- For a turbulent flow over a flat plate,
- The turbulent boundary layer continues to grow in thickness, with a small region below it called a viscous sublayer. In this sub layer, the flow is well behaved,just as the laminar boundary layer (Fig. 32.3)
- Observe that at a certain axial location, the laminar boundary layer tends to become unstable. Physically this means that the disturbances in the flow grow in amplitude at this location.
- Free stream turbulence, wall roughness and acoustic signals may be among the sources of such disturbances. Transition to turbulent flow is thus initiated with the instability in laminar flow.
- The possibility of instability in boundary layer was felt by Prandtl as early as 1912. The theoretical analysis of Tollmien and Schlichting showed that unstable waves could exist if the Reynolds number was 575.
The Reynolds number was defined as
where U∞ is the free stream velocity , δ* is the displacement thickness and v is the kinematic viscosity .
- Taylor developed an alternate theory, which assumed that the transition is caused by a momentary separation at the boundary layer associated with the free stream turbulence. In a pipe flow the initiation of turbulence is usually observed at Reynolds numbers (U∞, D/V )in the range of 2000 to 2700.
- The development starts with a laminar profile, undergoes a transition, changes over to turbulent profile and then stays turbulent thereafter (Fig. 32.4). The length of development is of the order of 25 to 40 diameters of the pipe.
Correlation Functions
A statistical correlation can be applied to fluctuating velocity terms in turbulence. Turbulent motion is by definition eddying motion. Not withstanding the circulation strength of the individual eddies, a high degree of correlation exists between the velocities at two points in space, if the distance between the points is smaller than the diameter of the eddy. Conversely, if the points are so far apart that the space, in between, corresponds to many eddy diameters (Figure 32.5), little correlation can be expected.
- Consider a statistical property of a random variable (velocity) at two points separated by a distance r. An Eulerian correlation tensor (nine terms) at the two points can be defined by
In other words, the dependence between the two velocities at two points is measured by the correlations, i.e. the time averages of the products of the quantities measured at two points. The correlation of the 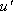 components of the turbulent velocity of these two points is defined as
components of the turbulent velocity of these two points is defined as
It is conventional to work with the non-dimensional form of the correlation, such as
A value of R(r) of unity signifies a perfect correlation of the two quantities involved and their motion is in phase.Negative value of the correlation function implies that the time averages of the velocities in the two correlated points have different signs. Figure 32.6 shows typical variations of the correlation R with increasing separation r .
- The positive correlation indicates that the fluid can be modelled as travelling in lumps. Since swirling motion is an essential feature of turbulent motion, these lumps are viewed as eddies of various sizes. The correlation R(r) is a measure of the strength of the eddies of size larger than r. Essentially the velocities at two points are correlated if they are located on the same eddy
- To describe the evolution of a fluctuating function u'(t), we need to know the manner in which the value of u' at different times are related. For this purpose the correlation function between the values of u' at different times is chosen and is called autocorrelation function.
- The correlation studies reveal that the turbulent motion is composed of eddies which are convected by the mean motion . The eddies have a wide range variation in their size. The size of the large eddies is comparable with the dimensions of the neighbouring objects or the dimensions of the flow passage.
- The size of the smallest eddies can be of the order of 1 mm or less. However, the smallest eddies are much larger than the molecular mean free paths and the turbulent motion does obey the principles of continuum mechanics.
|
56 videos|154 docs|75 tests
|
FAQs on Introduction to Turbulent Flow - 1 - Fluid Mechanics for Mechanical Engineering
| 1. What are the main characteristics of turbulent flow? |  |
| 2. How does laminar flow differ from turbulent flow? |  |
| 3. What factors influence the transition from laminar to turbulent flow? |  |
| 4. What are correlation functions, and how do they relate to turbulent flow? |  |
| 5. Why is understanding turbulent flow important in engineering and physics? |  |





















