Irodov Solutions: Constant Electric Field in Vacuum | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q1. Calculate the ratio of the electrostatic to gravitational interaction forces between two electrons, between two protons. At what value of the specific charge q/m of a particle would these forces become equal (in their absolute values) in the case of interaction of identical particles?
 View Answer
View Answer 
Ans 1.
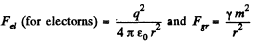
Thus 
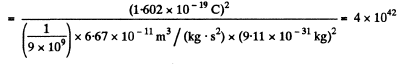
Similarly 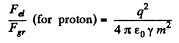
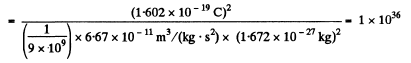
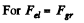
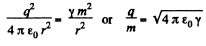
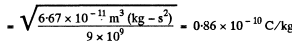
Q2. What would be the interaction force between two copper spheres, each of mass 1m, separated by the distance 1 m, if the total electronic charge in them differed from the total charge of the nuclei by one per cent?
 View Answer
View Answer 
Ans 2. Total number of atoms in the sphere of mass 1 gm 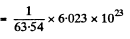
So the total nuclear charge 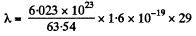
Now the charge on the sphere = Total nuclear charge - Total electronic charge
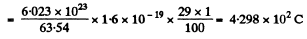
Hence force of interaction between these two spheres,
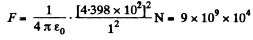
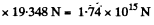
Q3. Two small equally charged spheres, each of mass m, are suspended from the same point by silk threads of length 1. The distance between the spheres x << 1. Find the rate dq/dt with which the charge leaks off each sphere if their approach velocity varies as 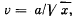 where a is a constant.
where a is a constant.
 View Answer
View Answer 
Ans 3. Let the balls be deviated by an angle θ, from the vertical w hen seperation between them equals x.
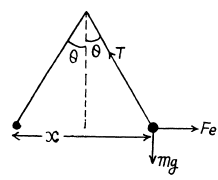
Applying Newton’s second law of motion for any one of the sphere, we get,
T cos θ = mg (1)
and T sin θ = Fe (2)
From the Eqs. (1) and (2)
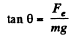
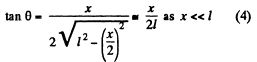
From Eqs. (3) and (4)
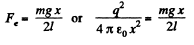
Thus 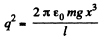 (5)
(5)
Differentiating Eqn. (5) with respect to time
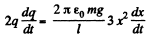
According to the problem 
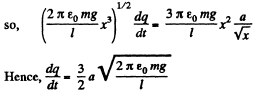
Q4. Two positive charges q1 and q2 are located at the points with radius vectors r1 and r2. Find a negative charge q3 and a radius vector r3 of the point at which it has to be placed for the force acting on each of the three charges to be equal to zero.
 View Answer
View Answer 
Ans 4. Let us choose coordinate axes as shown in the figure and fix three charges, q1 , q2 and q3 having position vectors  respectively.
respectively.
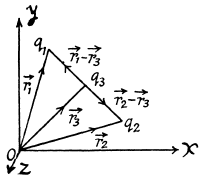
Now, for the equilibrium of q3
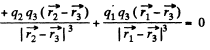
or, 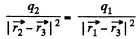
because 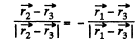
or, 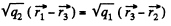
or, 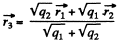
Also for the equilibrium of q1?
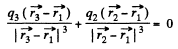
or, 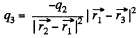
Substituting the value of 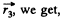
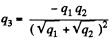
Q5. A thin wire ring of radius r has an electric charge q. What will be the increment of the force stretching the wire if a point charge q0 is placed at the ring's centre?
 View Answer
View Answer 
Ans 5. When the charge q0 is placed at the centre of the ring, the wire get stretched and the extra tension, produced in the wire, will balance the electric force due to the charge q0. Let the tension produced in the wire, after placing the charge q0, be T. From Newton’s second law in projection form Fn = mwn.
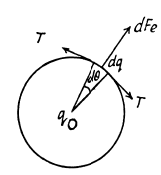
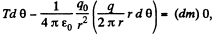
or, 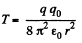
Q.6. A positive point charge 50 μC is located in the plane xy at the point with radius vector r0 = 2i + 3j, where i and j are the unit vectors of the x and y axes. Find the vector of the electric field strength E and its magnitude at the point with radius vector r = 8i — 5j. Here r0 and r are expressed in metres.
 View Answer
View Answer 
Ans6. Sought field strength

= 4.5 kV/m on putting the values.
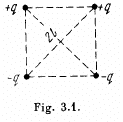
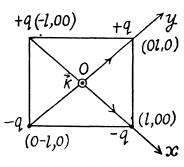
Q.7. Point charges q and —q are located at the vertices of a square with diagonals 2l as shown in Fig. 3.1. Find the magnitude of the electric field strength at a point located symmetrically with respect to the vertices of the square at a distance x from its centre.
 View Answer
View Answer 
Ans 7. Let us fix the coordinate system by taking the point of intersection of the diagonals as the origin and let  directed normally, emerging from the plane of figure.
directed normally, emerging from the plane of figure.
Hence the sought field strength :
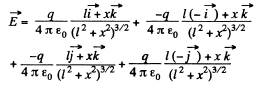
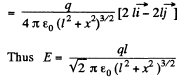
Q.8. A thin half-ring of radius R = 20 cm is uniformly charged with a total charge q = 0.70 nC. Find the magnitude of the electric field strength at the curvature centre of this half-ring.
 View Answer
View Answer 
Ans 8. From the symmetry of the problem the sought field.
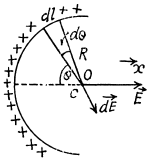
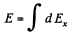
where the projection of field strength along x - axis due to an elemental charge is
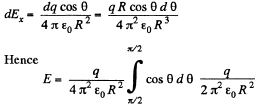
Q.9. A thin wire ring of radius r carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance l from its centre. Investigate the obtained function at 1 ≫ r. Find the maximum strength magnitude and the corresponding distance l. Draw the approximate plot of the function E(l).
 View Answer
View Answer 
Ans 9. From the symmetry of the condition, it is clear that, the field along the normal will be zero
i.e. 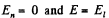
Now 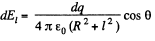
But 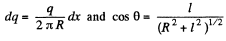
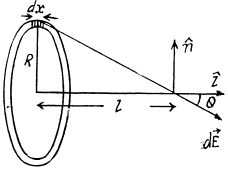
Hence 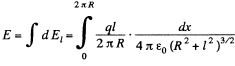
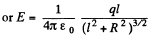
and for l ≫ R, the ring behaves like a point charge, reducing the field to the value,
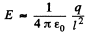
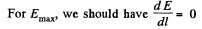
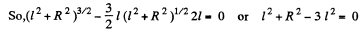
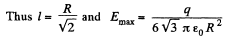
Q10. A point charge q is located at the centre of a thin ring of radius R with uniformly distributed charge —q. Find the magnitude of the electric field strength vector at the point lying on the axis of the ring at a distance x from its centre, if x ≫ R.
 View Answer
View Answer 
Ans 10. The electric potential at a distance a: from the given ring is given by,
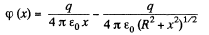
Hence, the field strength along x-axis (which is the net field strength in 'our case),
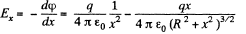
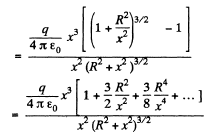
Neglecting the higher power of 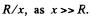
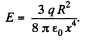
Note : Instead of φ (x), we may write E (x) directly using 3.9
Q11. A system consists of a thin charged wire ring of radius R and a very long uniformly charged thread oriented along the axis of the ring, with one of its ends coinciding with the centre of the ring. The total charge of the ring is equal to q. The charge of the thread (per unit length) is equal to λ. Find the interaction force between the ring and the thread.
 View Answer
View Answer 
Ans 11. From the solution of 3.9, the electric field strength due to ring at a point on its axis (say x-axis) at distance x from the centre of the ring is given by :

And from symmetry 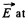 every point on the axis is directed along the x-axis (Fig.).
every point on the axis is directed along the x-axis (Fig.).
Let us consider an element (dx) on thread which carries the charge (λdx). The electric force experienced by the element in the field of ring.
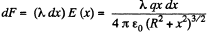
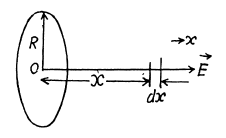
Thus the sought interaction
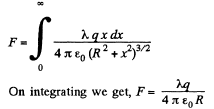
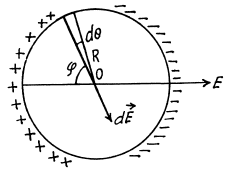
Q12. A thin nonconducting ring of radius R has a linear charge density λ = λ0 cos φ, where λ0 is a constant, φ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring;
(b) on the axis of the ring as a function of the distance x from its centre. Investigate the obtained function at x ≫ R.
 View Answer
View Answer 
Ans 12. (a) The g iven charge distribution is shown in Fig. The symmetry o f this distribution implies that vector 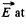 the point O is directed to the right, and its magnitude is equal to the sum of the projection onto the direction of
the point O is directed to the right, and its magnitude is equal to the sum of the projection onto the direction of 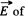 vectors
vectors 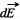 from elementary charges dq. The projection of vector
from elementary charges dq. The projection of vector 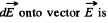
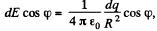
where 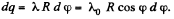
Integrating (1) over φ between 0 and 2 π we find the magnitude of the vector E:
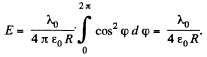
It should be noted that this integral is evaluated in the most simple way if we take into account that
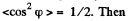
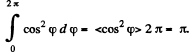
(b) Take an element S at an azimuthal angle φ from the x-axis, the element subtending an angle dφ at the centre.
The elementary field at P due to the element is
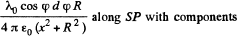
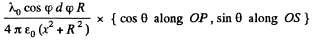
where 
The component along OP vanishes on integration as 
The component alon OS can be broken into the parts along OX and OY with
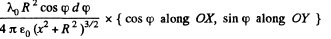
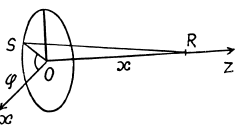
On integration, the part along OY vanishes. Finally
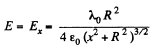
For x≫R

Q13. A thin straight rod of length 2a carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric field strength as a function of the distance r from the rod's centre along the straight line
(a) perpendicular to the rod and passing through its centre;
(b) coinciding with the rod's direction (at the points lying outside the rod). Investigate the obtained expressions at r ≫ a.
 View Answer
View Answer 
Ans 13. (a) It is clear from symmetry considerations that vector 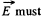 be directed as shown in the figure. This shows the way of solving this problem : we must find the component dEr of the field created by the element dl of the rod, having the charge dq and then integrate the result over all the elements of the rod. In this cas
be directed as shown in the figure. This shows the way of solving this problem : we must find the component dEr of the field created by the element dl of the rod, having the charge dq and then integrate the result over all the elements of the rod. In this cas
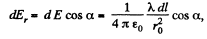
where 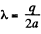 is the linear charge density. Let us reduce this equation of the form convenient for integration. Figure show s that dl cos
is the linear charge density. Let us reduce this equation of the form convenient for integration. Figure show s that dl cos 
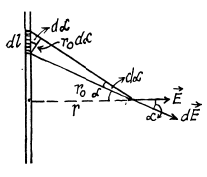
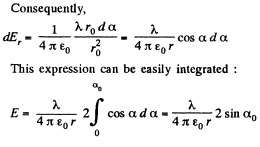
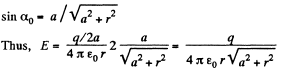
Note that in this case also 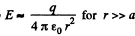 of the field of apoint charge.
of the field of apoint charge.
(b) Let, us consider the element of length dl at a distance l from the centre of the rod, as shown in the figure.
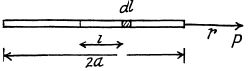
Then field at P, due to this element.
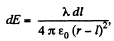
if the element lies on the side, shown in the diagram, and 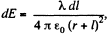 if it lies on other side.
if it lies on other side.
Hence 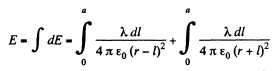
On integrating and putting 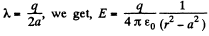
For 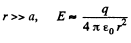
Q14. A very long straight uniformly charged thread carries a charge λ. per unit length. Find the magnitude and direction of the electric field strength at a point which is at a distance y from the thread and lies on the perpendicular passing through one of the thread's ends.
 View Answer
View Answer 
Ans 14. The problem is reduced to finding Ex and Ey viz . the projections of 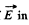 Fig, where it is assumed that λ > 0.
Fig, where it is assumed that λ > 0.
Let us start with Ex. The contribution to Ex. from the charge element of the segment dx is
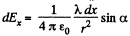 (1)
(1)
Let us reduce this expression to the form convenient for integration. In our case, dx = r Ja/cos α, r = y/cosα. Then
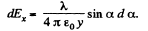
Integrating this expression over α between 0 and π/2, we find

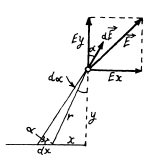
In order to find the projection Ey it is sufficient to recall that differs from dEx in that sin α in (1) is simply replaced
by cos α.
This gives
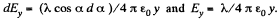 We have obtained an in teresting result :
We have obtained an in teresting result :
Ex = Ey in dependently of y,
i.e. 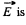 oriented at the angle of 45° to the rod. The modulus of
oriented at the angle of 45° to the rod. The modulus of 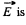
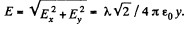
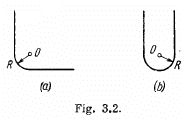
Q15. A thread carrying a uniform charge λ per unit length has the configurations shown in Fig. 3.2 a and b. Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude of the electric field strength at the point O.
 View Answer
View Answer 
Ans 15. (a) Using the solution of Q14, the net electric field strength at the point O due to straight parts of the thread equals zero. For the curved part (arc) let us derive a general expression i.e. let us calculate the field strength at the centre of arc of radius R and linear charge density λ and which subtends angle θ0 at the centre.
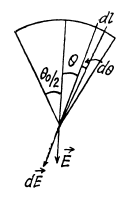
From the symmetry the sought field strength will be directed along the bisector of the angle θ0 and is given by
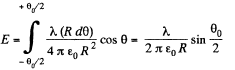
In our problem 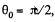 thus the field strength due to the turned part at the point
thus the field strength due to the turned part at the point 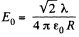 which is also the sought result.
which is also the sought result.
(b) Using the solution of 3.14 (a) , net field strength at O due to stright parts equals 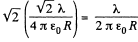 and is directed vertically down. Now using the solution of Q15
and is directed vertically down. Now using the solution of Q15
(a), field strength due to the given curved part (semi-circle) at the point O becomes  and is directed vertically upward. Hence the sought net field strengh becomes zero.
and is directed vertically upward. Hence the sought net field strengh becomes zero.
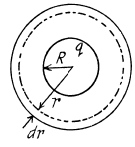
Q16. A sphere of radius r carries a surface charge of density σ = ar, where a is a constant vector, and r is the radius vector of a point of the sphere relative to its centre. Find the electric field strength vector at the centre of the sphere.
 View Answer
View Answer 
Ans 16. Given charge distribution on the surface  is shown in the figure. Symmetry of this distribution implies that the sought
is shown in the figure. Symmetry of this distribution implies that the sought 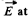 the centre O of the sphere is opposite to
the centre O of the sphere is opposite to 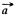
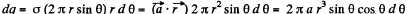
Again frgm symmetry, field strength due to any ring element 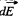 is also opposite to
is also opposite to 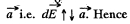
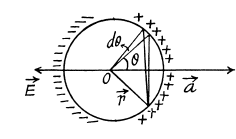
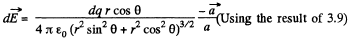
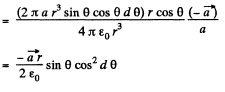
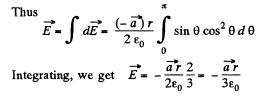
Q17. Suppose the surface charge density over a sphere of radius R depends on a polar angle θ as σ = σ0 cos θ, where σ0 is a positive constant. Show that such a charge distribution can be represented as a result of a small relative shift of two uniformly charged balls of radius R whose charges are equal in magnitude and opposite in sign. Resorting to this representation, find the electric field strength vector inside the given sphere.
 View Answer
View Answer 
Ans 17. We start from two charged spherical balls each of radius R with equal and opposite charge densities + p and - p. The centre of the balls are at 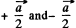 respectively so the equation of their surfaces are
respectively so the equation of their surfaces are 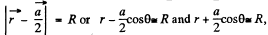 considering a to be small. The distance between the two surfaces in the radial direction at angle θ is
considering a to be small. The distance between the two surfaces in the radial direction at angle θ is 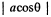 and does not depend on the azimuthal angle. It is seen from the diagram that the surface of the sphere has in effect a surface density
and does not depend on the azimuthal angle. It is seen from the diagram that the surface of the sphere has in effect a surface density 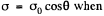
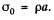
Inside any uniformly charged spherical ball, the field is radial and has the magnitude given by Gauss’s theorm
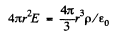
or 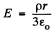
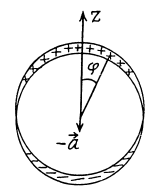
In vector notation, using the fact the V must be measured from the centre of the ball, we get, for the present case
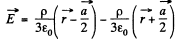
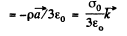
When 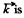 is the unit vector along the polar axis from which θ is measured.
is the unit vector along the polar axis from which θ is measured.
Q18. Find the electric field strength vector at the centre of a ball of radius R with volume charge density p = ar, where a is a constant vector, and r is a radius vector drawn from the ball's centre.
 View Answer
View Answer 
Ans 18. Let us consider an elemental spherical shell of thickness dr. Thus surface charge density of the shell 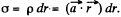
Thus using the solution of Q16, field strength due to this sperical shell
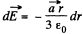
Hence the sought field strength
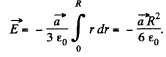
Q19. A very long uniformly charged thread oriented along the axis of a circle of radius R rests on its centre with one of the ends. The charge of the thread per unit length is equal to λ. Find the flux of the vector E across the circle area.
 View Answer
View Answer 
Ans 19. From the solution of Q14 field strength at a perpendicular distance r < R from its left end
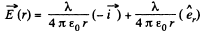
Here 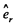 is a unit vector along radial direction.
is a unit vector along radial direction.
Let us consider an elemental surface, 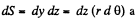 figure. Thus flux of
figure. Thus flux of 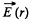 over the element
over the element 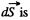 given by
given by
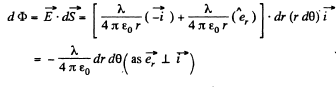
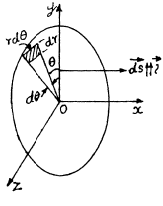
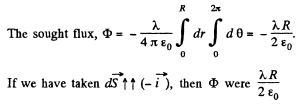
Hence 
Q20. Two point charges q and —q are separated by the distance 21 (Fig. 3.3). Find the flux of the electric field strength vector across a circle of radius R.
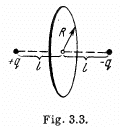
 View Answer
View Answer 
Ans 20. Let us consider an elemental surface area as shown in the figure. Then flux of the vector 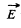 through the elemental area,
through the elemental area,
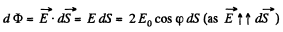
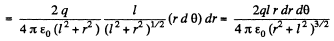
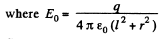 is magnitude of field strength due to any point charge at the point of location of considered elemental area.
is magnitude of field strength due to any point charge at the point of location of considered elemental area.
It can also be solved by considering a ring element or by using solid angle.
Q21. A ball of radius R is uniformly charged with the volume density p. Find the flux of the electric field strength vector across the ball's section formed by the plane located at a distance r0 < R from the centre of the ball.
 View Answer
View Answer 
Ans 21. Let us consider a ring element of radius x and thickness dx, as shown in the figure. Now, flux over the considered element,
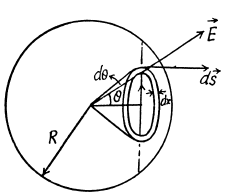
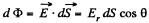
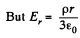 from Gauss's theorem,
from Gauss's theorem, 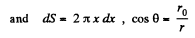
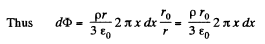
Hence sought flux
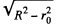
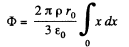
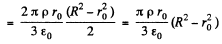
Q22. Each of the two long parallel threads carries a uniform charge per unit length. The threads are separated by a distance l. Find the maximum magnitude of the electric field strength in the symmetry plane of this system located between the threads.
 View Answer
View Answer 
Ans 22. The field at P due to the threads at A and B are both of magnitude 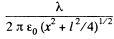 and directed along AP and BP. The resultant is along OP with
and directed along AP and BP. The resultant is along OP with
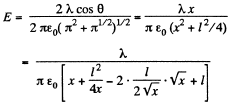
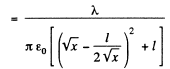
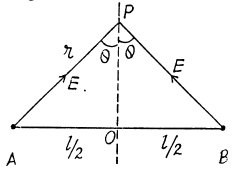
This is maximum when 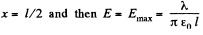
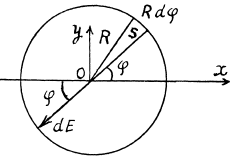
Q23. An infinitely long cylindrical surface of circular crosssection is uniformly charged lengthwise with the surface density σ = σ0 cos φ, where φ is the polar angle of the cylindrical coordinate system whose z axis coincides with the axis of the given surface. Find the magnitude and direction of the electric field strength vector on the z axis.
 View Answer
View Answer 
Ans 23. Take a section of the cylinder perpendicular to its axis through the point where the electric field is to be calculated. (All points on the axis are equivalent.) Consider an element S with azimuthal angle φ. The length of the element is R,dφ, R being the radius o f cross section of the cylinder. The element itself is a section of an infinite strip. The electric field at O due to this strip is
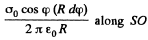
This can be resolved into
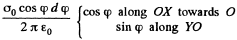
On integration the component along YO vanishes. What remains is
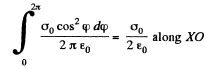
Q24. The electric field strength depends only on the x and y coordinates according to the law E = a (xi + yj)/(x2 + y2), where a is a constant, i and j are the unit vectors of the x and y axes. Find the flux of the vector E through a sphere of radius R with its centre at the origin of coordinates.
 View Answer
View Answer 
Ans 24. Since the field is axisymmetric (as the field of a uniformly charged filament ), we conclude that the flux through the sphere of radius R is equal to the flux through the lateral surface of a cylinder having the same radius and the height 2R, as arranged in the figure.
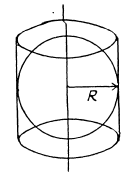
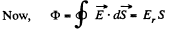
But 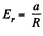
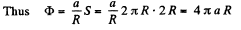
Q25. A ball of` radius R carries a positive charge whose volume density depends only on a separation r from the ball's centre as P = p0 (1 — r/R), where P0 is a constant. Assuming the permittivities of the ball and the environment to be equal to unity, find:
(a) the magnitude of the electric field strength as a function of the distance r both inside and outside the ball;
(b) the maximum intensity Emax and the corresponding distance rm.
 View Answer
View Answer 
Ans 25. (a) Let us consider a sphere of radius r < R then charge, inclosed by the considered sphere,
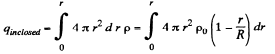 (1)
(1)
Now, applying Gauss’ theorem,
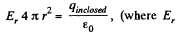 is the projection o f electric field along the radial lin e.)
is the projection o f electric field along the radial lin e.)
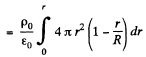
or, 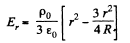
And for a point, outside the sphere r > R.
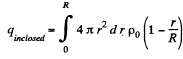 (as there is no charge outside the ball)
(as there is no charge outside the ball)
Again from Gauss’ theorem,
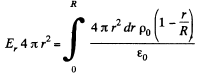
or, 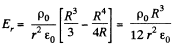
(b) As‘magnitude of electric field decreases with increasing r for r > R, field will be maximum for r < R. Now, for Er to be maximum

Hence 
Q26. A system consists of a ball of radius R carrying a spherically symmetric charge and the surrounding space filled with a charge of volume density p = α/r, where α is a constant, r is the distance from the centre of the ball. Find the ball's charge at which the magnitude of the electric field strength vector is independent of r outside the ball. How high is this strength? The permittivities of the ball and the surrounding space are assumed to be equal to unity.
 View Answer
View Answer 
Ans 26. Let the charge carried by the sphere be q, then using Gauss’ theorem for a spherical surface having radius r > R, we can write.
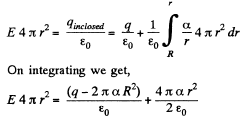
The intensity E does not depend on r when the experession in the parentheses is equal to zero. Hence
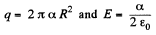
Q27. A space is filled up with a charge with volume density 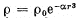 , where P0 and α are positive constants, r is the distance from the centre of this system. Find the magnitude of the electric field strength vector as a function of r. Investigate the obtained expression for the small and large values of r, i.e. at αr3 ≪1 and αr3 ≫ 1.
, where P0 and α are positive constants, r is the distance from the centre of this system. Find the magnitude of the electric field strength vector as a function of r. Investigate the obtained expression for the small and large values of r, i.e. at αr3 ≪1 and αr3 ≫ 1.
 View Answer
View Answer 
Ans 27. Let us consider a spherical layer of radius r and thickness dr, having its centre coinciding with the centre of the system. Then using Gauss’ theorem for this surface,
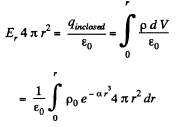
After integration
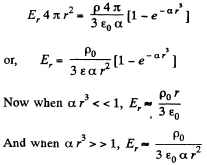
Q28. Inside a ball charged uniformly with volume density p there is a spherical cavity. The centre of the cavity is displaced with respect to the centre of the ball by a distance a. Find the field strength E inside the cavity, assuming the permittivity equal to unity.
 View Answer
View Answer 
Ans 28. Using Gauss theorem we can easily show that the electric field strength within a uniformly charged sphere is 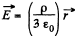
The cavity, in our problem, may be considered as the superposition of two balls, one with the charge density p and the other with - p.
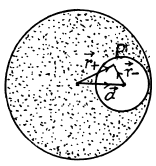
Let P be a point inside the cavity such that its position vector with respect to the centre of cavity be 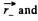 with respect to the centre of the ball
with respect to the centre of the ball 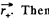 Then from the principle of superposition, field inside the cavity, at an arbitrary point P ,
Then from the principle of superposition, field inside the cavity, at an arbitrary point P ,
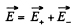
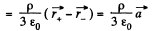
Note : Obtained expression for 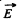 shows that it is valid regardless of the ratio between the radii of the sphere and the distance between their centres.
shows that it is valid regardless of the ratio between the radii of the sphere and the distance between their centres.
Q29. Inside an infinitely long circular cylinder charged uniformly with volume density p there is a circular cylindrical cavity. The distance between the axes of the cylinder and the cavity is equal to a. Find the electric field strength E inside the cavity. The permittivity is assumed to be equal to unity.
 View Answer
View Answer 
Ans 29. Let us consider a cylinderical Gaussian surface of radius r and height h inside an infinitely long charged cylinder with charge density p. Now from Gauss theorem :
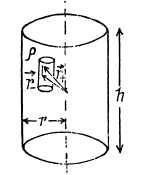
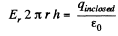
(where Er is the field inside the cylinder at a distance r from its axis.)
or, 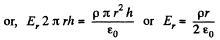
Now, using the method of Q.28 field at a point P, inside the cavity, is
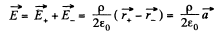
Q30. There are two thin wire rings, each of radius R, whose axes coincide. The charges of the rings are q and —q. Find the potential difference between the centres of the rings separated by a distance a.
 View Answer
View Answer 
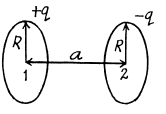
Ans 30. The arrangement of the rings are as shown in the figure. Now, potential at the point 1, φ1 = potential at 1 due to the ring 1 + potential at 1 due to the ring 2.
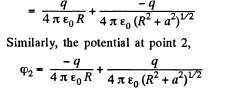
Hence, the sought potential difference,
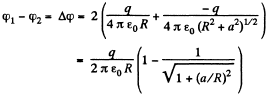
Q31. There is an infinitely long straight thread carrying a charge with linear density λ, = 0.40 μC/m. Calculate the potential difference between points 1 and 2 if point 2 is removed η = 2.0 times farther from the thread than point I.
 View Answer
View Answer 
Ans 31. We know from Gauss theorem that the electric field due to an infinietly long straight wire, at a perpendicular distance r from it equals, 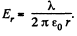 So, the work done is
So, the work done is
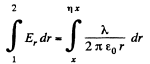
(where x is perpendicular distance from the thread by which point 1 is removed from it.)
Hence 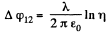
Q32. Find the electric field potential and strength at the centre of a hemisphere of radius R charged uniformly with the surface density σ.
 View Answer
View Answer 
Ans 32. Let us consider a ring element as shown in the figure. Then the charge, carried by the element, 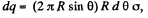

Hence, the potential due to the considered element at the centre of the hemisphere,
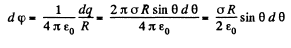
So potential due to the whole hemisphere
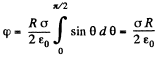
Now from the symmetry of the problem, net electric field of the hemisphere is directed towards the negative y - axis. We have
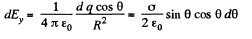
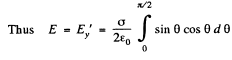
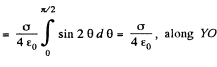
Q33. A very thin round plate of radius R carrying a uniform surface charge density a is located in vacuum. Find the electric field potential and strength along the plate's axis as a function of a distance l from its centre. Investigate the obtained expression at l → 0 and l ≫ R.
 View Answer
View Answer 
Ans 33. Let us consider an elementary ring of thickness dy and radius y as shown in the figure. Then potential at a point P, at distance l from the centre of the disc, is
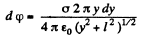
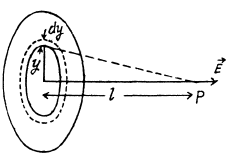
Hence potential due to the whole disc,
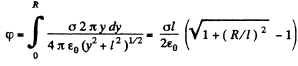
From symmetry
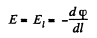
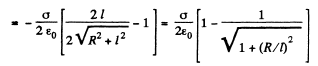
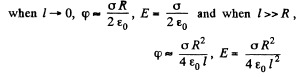
Q34. Find the potential φ at the edge of a thin disc of radius R carrying the uniformly distributed charge with surface density σ.
 View Answer
View Answer 
Ans 34. By definition, the potential in the case of a surface charge distribution is defined by integral 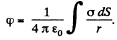 In order to simplify integration, we shall choose the area element dS in the form of a part of the ring of radius r and width dr in (Fig.). Then dS - 2θ r dr, r = 2R cos θ and dr = - 2R sin θ d θ. After substituting these expressions into integral
In order to simplify integration, we shall choose the area element dS in the form of a part of the ring of radius r and width dr in (Fig.). Then dS - 2θ r dr, r = 2R cos θ and dr = - 2R sin θ d θ. After substituting these expressions into integral
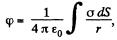 we obtain the expression for cp at the point O:
we obtain the expression for cp at the point O:
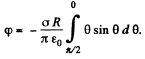
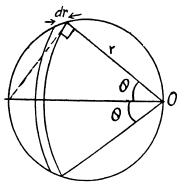
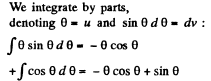
which gives -1 after substituting the limits of integration. As a result, we obtain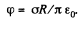
Q35. Find the electric field strength vector if the potential of this field has the form φ = ar, where a is a constant vector, and r is the radius vector of a point of the field.
 View Answer
View Answer 
Ans 35. In accordance with the problem 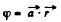
Thus from the equation 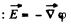
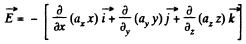
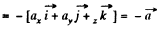
Q36. Determine the electric field strength vector if the potential of this field depends on x, y coordinates as
(a) φ = a (x2 — y2);
(b) φ = axy,
where a is a constant. Draw the approximate shape of these fields .using lines of force (in the x, y plane).
 View Answer
View Answer 
Ans 36. 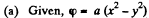
So, 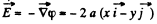
The sought shape of field lines is as shown in the figure (a) of answersheet assuming a > 0:
(b) Since φ = axy
So, 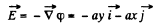
Plot as shown in the figure (b) of answersheet
Q37. The potential of a certain electrostatic field has the form cp = a (x2 + y2) + bz2, where a and b are constants. Find the magnitude and direction of the electric field strength vector. What shape have the equipotential surfaces in the following cases:
(a) a > 0, b> 0; (b) a > 0, b < 0?
 View Answer
View Answer 
Ans 37. 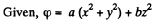
So, 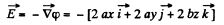
Hence 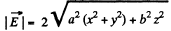
Shape of the equipotential surface :
Put 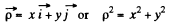
Then the equipotential surface has the equation
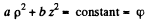
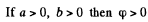 and the equation of the equipotential surface is
and the equation of the equipotential surface is
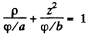
which is an ellipse in p , z coordinates. In three dimensions the surface is an ellipsoid of revolution with semi- axis 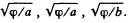
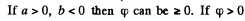 then the equation is
then the equation is
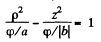
This is a single cavity hyperboloid of revolution about z axis. If φ = 0 then
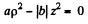
or 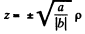
is the equation of a right circular cone.
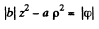
or 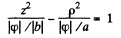
This is a two cavity hyperboloid of revolution about z-axis.
Q38. A charge q is uniformly distributed over the volume of a sphere of radius R. Assuming the permittivity to be equal to unity throughout, find the potential
(a) at the centre of the sphere;
(b) inside the sphere as a function of the distance r from its centre.
 View Answer
View Answer 
Ans 38. From Gauss’ theorem intensity at a point, inside the sphere at a distance r from the centre is given by, 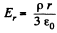 and outside it, is given by
and outside it, is given by 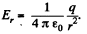
(a) Potential at the centre of the sphere,
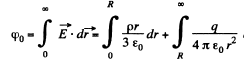
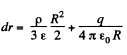
as 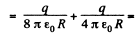
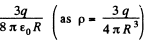
(b) Now, potential at any point, inside the sphere, at a distance r from it s centre.
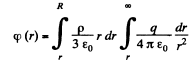
On integration : 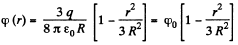
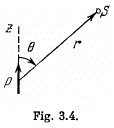
Q39. Demonstrate that the potential of the field generated by a dipole with the electric moment p (Fig. 3.4) may be represented as 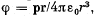 where r is the radius vector. Using this expression, find the magnitude of the electric field strength vector as a function of r and θ.
where r is the radius vector. Using this expression, find the magnitude of the electric field strength vector as a function of r and θ.
 View Answer
View Answer 
Ans 39. Let two charges +q and - q be separated by a distance l. Then electric potential at a point at distance r > > l from this dipole,
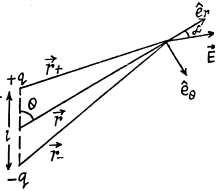
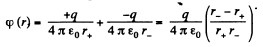 (1)
(1)
But 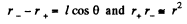
From Eqs. (1) and (2),
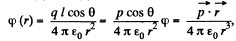
where p is magnitude of electric moment vector.
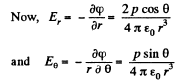
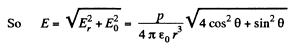
Q40. A point dipole with an electric moment p oriented in the positive direction of the z axis is located at the origin of coordinates. Find the projections Ez and E⊥ of the electric field strength vector (on the plane perpendicular to the z axis at the point S (see Fig. 3.4)). At which points is E perpendicular to p?

 View Answer
View Answer 
Ans 40. From the results, obtained in the previous problem,
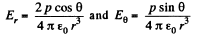
From the given figure, it is clear that,
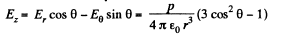
and 
When 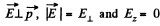
So 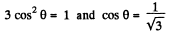
Thus 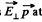 the points located on the lateral surface of the cone, having its axis, coinciding with the direction of z-axis and semi vertex angle
the points located on the lateral surface of the cone, having its axis, coinciding with the direction of z-axis and semi vertex angle 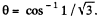
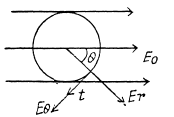
Q41. A point electric dipole with a moment p is placed in the external uniform electric field whose strength equals E0, with 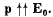 In this case one of the equipotential surfaces enclosing the dipole forms a sphere. Find the radius of this sphere.
In this case one of the equipotential surfaces enclosing the dipole forms a sphere. Find the radius of this sphere.
 View Answer
View Answer 
Ans 41. Let us assume that the dipole is at the centre of the one equipotential surface which is spherical (Fig.)* On an equipotential surface the net electric field strength along the tangent of it becomes zero. Thus
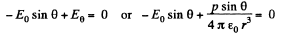
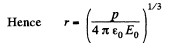
Alternate : Potential at the point, near the dipole is given by,
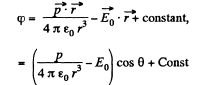
For φ to be constant,

Thus 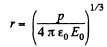
Q42. Two thin parallel threads carry a uniform charge with linear densities λ and —λ. The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r ≫ l at the angle θ to the vector l (Fig. 3.5).

 View Answer
View Answer 
Ans 42. Let P be a point, at distace r >> l and at an angle to θ the vector 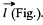
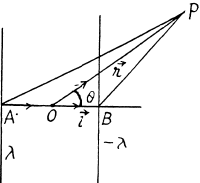
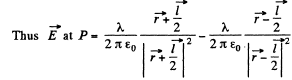
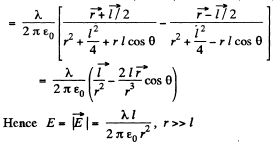
Also, 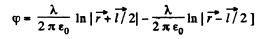
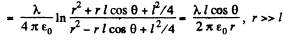
Q43. Two coaxial rings, each of radius R, made of thin wire are separated by a small distance l (l ≪ R) and carry the charges q and —q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (Fig. 3.6). Show in the same drawing the approximate plots of the functions obtained. Investigate these functions at |x| ≫ R.
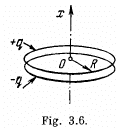
 View Answer
View Answer 
Ans 43. The potential can be calculated by superposition. Choose the plane of the upper ring as x = l/2 and that of the lower ring as x = - l/2.
Then 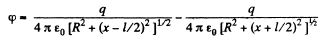
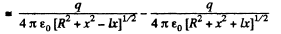
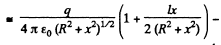
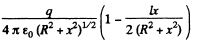
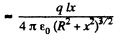
For 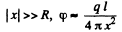
The electric field is 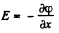
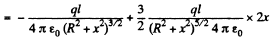
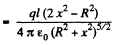
For  The plot is as given in the book.
The plot is as given in the book.
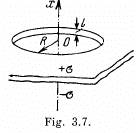
Q44. Two infinite planes separated by a distance l carry a uniform surface charge of densities σ and —σ (Fig. 3.7). The planes have round coaxial holes of radius R, with 1 ≪ R. Taking the origin O and the x coordinate axis as shown in the figure, find the potential of the electric field and the projection of its strength vector Ex on the axes of the system as functions of the x coordinate. Draw the approximate plot φ (x).
 View Answer
View Answer 
Ans 44. The field of a pair of oppositely chaiged sheets with holes can by superposition be reduced to that of a pair of uniform opposite charged sheets and discs with opposite charges. Now the charged sheets do not contribute any field outside them. Thus using the result of the previous problem
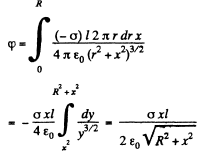

The plot is as shown in the answersheet.
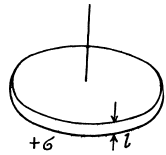
Q45. An electric capacitor consists of thin round parallel plates, each of radius R, separated by a distance l (l ≪ R) and uniformly charged with surface densities σ and —σ. Find the potential of the electric field and the magnitude of its strength vector at the axes of the capacitor as functions of a distance x from the plates if x ≫ l. Investigate the obtained expressions at x ≫ R.
 View Answer
View Answer 
Ans 45. For x > 0 we can use the result as given above and write
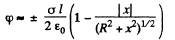
for the solution that vanishes at α. There is a discontinuity in potential for |x| = 0. The solution for negative x is obtained by σ → -σ. Thus
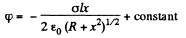
Hence ignoring the jump
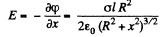
for large 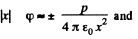
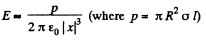
Q46. A dipole with an electric moment p is located at a distance r from a long thread charged uniformly with a linear density λ. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread;
(b) along the radius vector r;
(c) at right angles to the thread and the radius vector r.
 View Answer
View Answer 
Ans 46. 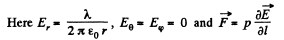
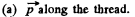
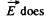 not change as the point of observation is moved along the thread.
not change as the point of observation is moved along the thread.
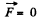
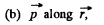

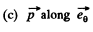
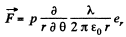
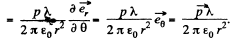
Q47. Find the interaction force between two water molecules separated by a distance l = 10 nm if their electric moments are oriented along the same straight line. The moment of each molecule equals p = 0.62.10-29 C • m.
 View Answer
View Answer 
Ans 47. Force on a dipole of moment p is given by,
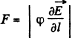
In our problem, field, due to a dipole at a distance l, where a dipole is placed,
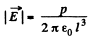
Hence, the force of interaction,
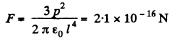
Q48. Find the potential φ (x, y) of an electrostatic field E = a (yi xj), where a is a constant, i and j are the unit vectors of the x and y axes.
 View Answer
View Answer 
Ans 48.
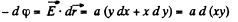
On integrating, 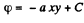
Q49. Find the potential φ (x, y) of an electrostatic field E = 2axyi + a (x2 — y2) j, where a is a constant, i and j are the unit vectors of the x and y axes.
 View Answer
View Answer 
Ans 49.

or 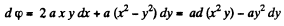
On integrating, we get,
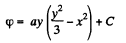
Q50. Determine the potential φ (x, y, z) of an electrostatic field E = ayi (ax + bz) j + byk, where a and b are constants, i, j, k are the unit vectors of the axes x, y, z.
 View Answer
View Answer 
Ans 50. Given, again
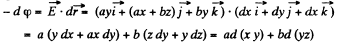
On integrating,
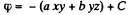
Q51. The field potential in a certain region of space depends only on the x coordinate as φ = — ax3 + b, where a and b are constants. Find the distribution of the space charge p (x).
 View Answer
View Answer 
Ans 51. Field intensity along x-axis.
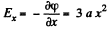 (1)
(1)
Then using Gauss’s theorem in differential from
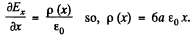
Q52. A uniformly distributed space charge fills up the space between two large parallel plates separated by a distance d. The potential difference between the plates is equal to Δφ. At what value of charge density p is the field strength in the vicinity of one of the plates equal to zero? What will then be the field strength near the other plate?
 View Answer
View Answer 
Ans 52. In the space between the plates we have the Poisson equation
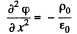
or, 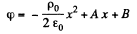
where p0 is the constant space charge density between the plates.
We can choose 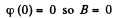
Then 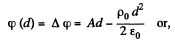
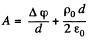
Now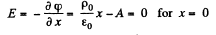
if 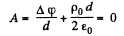
then 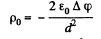
Also 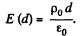
Q53. The field potential inside a charged ball depends only on the distance from its centre as φ = ar2 + b, where a and b are constants. Find the space charge distribution p (r) inside the ball.
 View Answer
View Answer 
Ans 53. Field intensity is along radial line and is
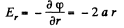 (1)
(1)
From the Gauss’ theorem,
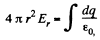
where dq is the charge contained between the sphere of radii r and r + dr.
Hence  (2)
(2)
Differentiating 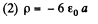
FAQs on Irodov Solutions: Constant Electric Field in Vacuum - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is a constant electric field in vacuum and how is it created? |  |
| 2. How does a constant electric field affect a charged particle in vacuum? |  |
| 3. What is the mathematical expression for a constant electric field in vacuum? |  |
| 4. What are the characteristics of electric field lines in a constant electric field? |  |
| 5. How can we visualize the effects of a constant electric field on a test charge? |  |

















