Irodov Solutions: Dynamics of A Solid Body- 4 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q. 281. A horizontally oriented uniform rod AB of mass m = 1.40 kg and length l0 = 100 cm rotates freely about a stationary vertical axis OO' passing through its end A. The point A is located at the middle of the axis OO' whose length is equal to l = 55 cm. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis OO' is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
Solution. 281. The total centrifugal force can be calculated by,
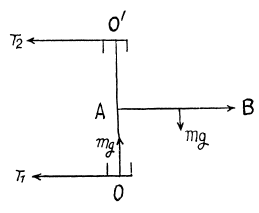
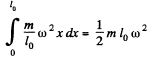
Then for equilibrium
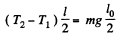
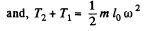
Thus T1 vanishes, when
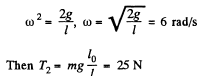
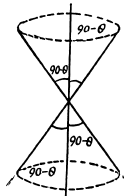
Q. 282. The middle of a uniform rod of mass m and length l is rigidly fixed to a vertical axis OO' so that the angle between the rod and the axis is equal to θ (see Fig. 1.71). The ends of the axis OO' are provided with bearings. The system rotates without friction with an angular velocity ω. Find:
(a) the magnitude and direction of the rod's angular momentum M relative to the point C, as well as its angular momentum relative to the rotation axis;
(b) how much the modulus of the vector M relative to the point C increases during a half-turn;
(c) the moment of external forces N acting on the axle OO' in the process of rotation
Solution. 282. See the diagram in the book (Fig. 1.71).
(a) The angular velocity 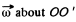 can be resolved into a component parallel to the rod and a component co sin0 perpendicular to the rod through C. The component parallel to the rod does not contribute so the angular momentum
can be resolved into a component parallel to the rod and a component co sin0 perpendicular to the rod through C. The component parallel to the rod does not contribute so the angular momentum
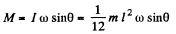
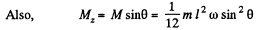
This can be obtained directly also,
(b) The modulus of  does not change but the modulus of the change of
does not change but the modulus of the change of 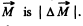
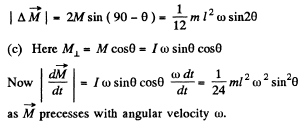
Q. 283. A top of mass m = 0.50 kg, whose axis is tilted by an angle θ = 30° to the vertical, precesses due to gravity. The moment of inertia of the top relative to its symmetry axis is equal to I = 2.0 g•m2 , the angular velocity of rotation about that axis is equal to ω = 350 rad/s, the distance from the point of rest to the centre of inertia of the top is l = 10 cm. Find:
(a) the angular velocity of the top's precession;
(b) the magnitude and direction of the horizontal component of the reaction force acting on the top at the point of rest
Solution. 283. Here M = I ω is along the symmetry axis. It has tw o components, the part l ω cosθ is constant and the part M⊥ - l ω sinθ presesses, then
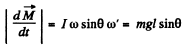
or, 
(b) This force is the centripetal force due to precession. It acls inward and has the magnitude
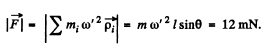
 the distance of the i th element from the axis. This is the force that the table will exert on the top. See the diagram in the answer sheet
the distance of the i th element from the axis. This is the force that the table will exert on the top. See the diagram in the answer sheet

Q. 284. A gyroscope, a uniform disc of radius R = 5.0 cm at the end of a rod of length l = 10 cm (Fig. 1.73), is mounted on the floor of an elevator car going up with a constant acceleration w = 2.0 m/s2. The other end of the rod is hinged at the point O. The gyroscope precesses with an angular velocity n = 0.5 rps. Neglecting the friction and the mass of the rod, find the proper angular velocity of the disc.
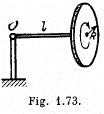
Solution. 284. See the diagram in the book (Fig. 1.73).
The moment of inertia of the disc about its symmentry axis is 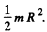 If the angular velocity of the disc is co then the angular momentum is
If the angular velocity of the disc is co then the angular momentum is 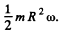 The precession frequency being 2 π n,
The precession frequency being 2 π n,
we have 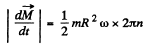
This must equal m (g + w) l, the effective gravitational torques (g being replaced by g + w in the elevator). Thus,
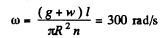
Q. 285. A top of mass m = 1.0 kg and moment of inertia relative to its own axis I = 4.0 g•m2 spins with an angular velocity ω = 310 rad/s. Its point of rest is located on a block which is shifted in a horizontal direction with a constant acceleration w = 1.0 m/s2. The distance between the point of rest and the centre of inertia of the top equals l = 10 cm. Find the magnitude and direction of the angular velocity of precession ω'.
Solution. 285. The effective g is 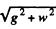 inclined at angle
inclined at angle 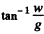 with the vertical. Then with reference to the new " vertical" we proceed as in problem 1.283. Thu
with the vertical. Then with reference to the new " vertical" we proceed as in problem 1.283. Thu
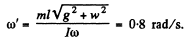
The vector 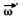 forms an angle
forms an angle 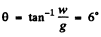 with the normal vertical.
with the normal vertical.
Q. 286. A uniform sphere of mass m = 5.0 kg and radius R = 6.0 cm rotates with an angular velocity ω = 1250 rad/s about a horizontal axle passing through its centre and fixed on the mounting base by means of bearings. The distance between the bearings equals l = 15 cm. The base is set in rotation about a vertical axis with an angular velocity ω' = 5.0 rad/s. Find the modulus and direction of the gyroscopic forces.
Solution. 286. The moment of inertia of the sphere is 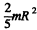 and hence the value of angular momentum is
and hence the value of angular momentum is 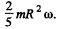 Since it precesses at speed ω' the torque required is
Since it precesses at speed ω' the torque required is
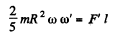
So, 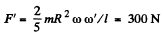
(The force F ' must be vertical.)
Q. 287. A cylindrical disc of a gyroscope of mass m = 15 kg and radius r = 5.0 cm spins with an angular velocity ω = 330 rad/s. The distance between the bearings in which the axle of the disc is mounted is equal to l = 15 cm. The axle is forced to oscillate about a horizontal axis with a period T = 1.0 s and amplitude φm, = 20°. Find the maximum value of the gyroscopic forces exerted by the axle on the bearings.
Solution. 287. The moment of inertia is 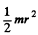 and angular momentum is
and angular momentum is 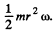 The axle oscillates about a horizontal axis making an instantaneous angle.
The axle oscillates about a horizontal axis making an instantaneous angle.
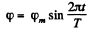
This means that there is a variable precession with a rate of precession 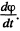 The maximum value of this is
The maximum value of this is 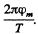 When the angle between the axle and the axis is at its maximumis value, a torque
When the angle between the axle and the axis is at its maximumis value, a torque 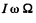
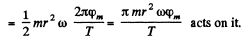
The corresponding gyroscopic force will be 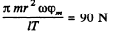
Q. 288. A ship moves with velocity v = 36 km per hour along an arc of a circle of radius R = 200 m. Find the moment of the gyroscopic forces exerted on the bearings by the shaft with a flywheel whose moment of inertia relative to the rotation axis equals I = 3.8.103 kg•m2 and whose rotation velocity n = 300 rpm. The rotation axis is oriented along the length of the ship.
Solution. 288. The revolutions per minute of the flywheel being n, the angular momentum of the flywheel

Q. 289. A locomotive is propelled by a turbine whose axle is parallel to the axes of wheels. The turbine's rotation direction coincides with that of wheels. The moment of inertia of the turbine rotor relative to its own axis is equal to I = 240 kg• m2 . Find the additional force exerted by the gyroscopic forces on the rails when the locomotive moves along a circle of radius R = 250 m with velocity v = 50 km per hour. The gauge is equal to l = 1.5 m. The angular velocity of the turbine equals n = 1500 rpm.
Solution. 289. As in the previous problem a couple 2πInv/R must come in play. This can be done if a force, 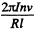 acts on the rails in opposite directions in addition to the centrifugal and other forces. The force on the outer rail is increased and that on the inner rail decreased. The additional force in this case has the magnitude 1.4 kN.m.
acts on the rails in opposite directions in addition to the centrifugal and other forces. The force on the outer rail is increased and that on the inner rail decreased. The additional force in this case has the magnitude 1.4 kN.m.
FAQs on Irodov Solutions: Dynamics of A Solid Body- 4 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are the main topics covered in Irodov Solutions: Dynamics of a Solid Body-4 NEET? |  |
| 2. How can I effectively prepare for the dynamics section in NEET using Irodov Solutions: Dynamics of a Solid Body-4 NEET? |  |
| 3. Are the solutions provided in Irodov Solutions: Dynamics of a Solid Body-4 NEET step-by-step and easy to understand? |  |
| 4. Can I rely solely on Irodov Solutions: Dynamics of a Solid Body-4 NEET for my NEET preparation? |  |
| 5. Where can I find Irodov Solutions: Dynamics of a Solid Body-4 NEET for practice and preparation? |  |
















