Q. 173. A mercury drop shaped as a round tablet of radius R and thickness h is located between two horizontal glass plates. Assuming that h ≪ R , find the mass m of a weight which has to be placed on the upper plate to diminish the distance between the plates n-times. The contact angle equals θ. Calculate m if R = 2.0 cm, h = 0.38 mm, n = 2.0, and θ = 135°.
Solution. 173. We must first calculate the pressure difference inside the film from that outside. This is

Here 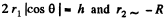 the radius of the tablet and can be neglected. Thus the total force exerted by mercury drop on the upper glass plate i
the radius of the tablet and can be neglected. Thus the total force exerted by mercury drop on the upper glass plate i
We should put h / n for h because the tablet is com presed n times. Then since Hg is nearly, in com pressible, 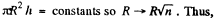
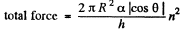
Part of the force is needed to keep the Hg in the shape of a table rather than in the shape of infinitely thin sheet. This part can be calculated being putting n = 1 above. Thus
or 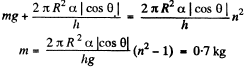
Q. 174. Find the attraction force between two parallel glass plates, separated by a distance h = 0.10 mm, after a water drop of mass m = 70 mg was introduced between them. The wetting is assumed to be complete.
Solution. 174. The pressure inside the film is less than that outside by an amount a  where r1 and r2 are the principal radii of curvature of the meniscus. One of these is small being given by
where r1 and r2 are the principal radii of curvature of the meniscus. One of these is small being given by 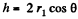 while the other is large and will be ignored. Then
while the other is large and will be ignored. Then  where A = area of the water film between the plates.
where A = area of the water film between the plates.
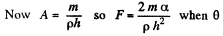 (the angle of contact) = 0
(the angle of contact) = 0
Q. 175. Two glass discs of radius R = 5.0 cm were wetted with water and put together so that the thickness of the water layer between them was h = 1.9 p.m. Assuming the wetting to he complete, find the force that has to be applied at right angles to the plates in order to pull them apart.
Solution. 175. This is analogous to the previous problem except that : A = π R2
So 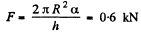
Q. 176. Two vertical parallel glass plates are partially submerged in water. The distance between the plates is d = 0.10 mm, and their width is l = 12 cm. Assuming that the water between the plates does not reach the upper edges of the plates and that the wetting is complete, find the force of their mutual attraction.
Solution. 176. The energy of the liquid between the plates is
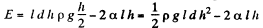
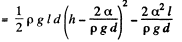
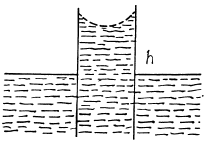
This energy is minimum when, 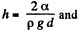 the minimum potential energy is the
the minimum potential energy is the 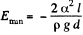
The force of attraction between the plates can be obtained fro m this as
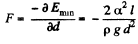 (minus sign means the force is attractive.)
(minus sign means the force is attractive.)
Thus 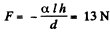
Q. 177. Find the lifetime of a soap bubble of radius R connected with the atmosphere through a capillary of length l and inside radius r. The surface tension is α, the viscosity coefficient of the gas is η.
Solution. 177. Suppose the radius of the bubble is x at some instant. Then the pressure inside is 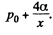 The flow through the capillary is by Poiseuille’s equation,
The flow through the capillary is by Poiseuille’s equation,
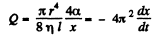
Integrating 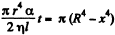 where we have used the fact that t = 0 where x = R.
where we have used the fact that t = 0 where x = R.
This gives 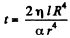 as the life time of the bubble corresponding to x = 0
as the life time of the bubble corresponding to x = 0
Q. 178. A vertical capillary is brought in contact with the water surface. What amount of heat is liberated while the water rises along the capillary? The wetting is assumed to be complete, the surface tension equals α.
Solution. 178. If the liquid rises to a height h', the energy of the liquid column becomes
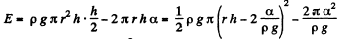
This is minimum when  and that is relevant height to which water must rise.
and that is relevant height to which water must rise.
At this point, 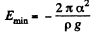
Since E = 0 in the absence o f surface tension a heat 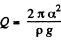 must have been liberated.
must have been liberated.
Q. 179. Find the free energy of the surface layer of
(a) a mercury droplet of diameter d = 1.4 mm;
(b) a soap bubble of diameter d = 6.0 mm if the surface tension of the soap water solution is equal to α = 45 mN/m.
Solution. 179. (a) The free energy per unit area being α,
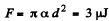
(b)  because the soap bubble has two surfaces. Substitution gives
because the soap bubble has two surfaces. Substitution gives 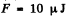
Q. 180. Find the increment of the free energy of the surface layer when two identical mercury droplets, each of diameter d = 1.5 mm, merge isothermally.
Solution. 180. When two mercury drops each of diameter d merge, the resulting drop has diameter d1
where 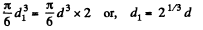
The increase in free energy is
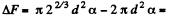
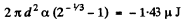
Q. 181. Find the work to be performed in order to blow a soap bubble of radius R if the outside air pressure is equal to p0 and the surface tension of the soap water solution is equal to α.
Solution. 181. Work must be done to stretch the soap film and compress the air inside. The former is simply  here being two sides o f the film. To get the latter we note that the compression is isothermal and work done is
here being two sides o f the film. To get the latter we note that the compression is isothermal and work done is
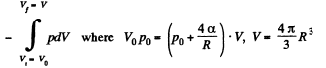
or 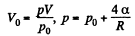
and minus sign is needed becaue we are calculating work done on the system. Thus since pV remains constants, the work done is
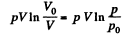
So 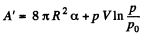
Q. 182. A soap bubble of radius r is inflated with an ideal gas. The atmospheric pressure is p0, the surface tension of the soap water solution is α. Find the difference between the molar heat capacity of the gas during its heating inside the bubble and the molar heat capacity of the gas under constant pressure, C — Cp.
Solution. 182. When heat is given to a soap bubble the temperature of the air inside rises and the bubble expands but unless the bubble bursts, the amount of air inside does not change. Further we shall neglect the variation of the surface tension with temperature. Then from the gas equations
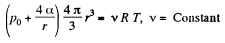
Differentiating
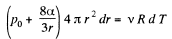
or 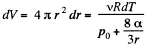
Now from the first law
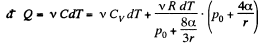
or 
using 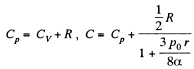
Q. 183. Considering the Carnot cycle as applied to a liquid film, show that in an isothermal process the amount of heat required for the formation of a unit area of the surface layer is equal to q = —T•dα/dT, where dα/dT is the temperature derivative of the surface tension.
Solution. 183. Consider an infinitesimal Carnot cycle with isotherms at T - dT and T. Let A be the work done during the cycle. Then

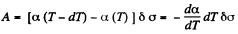
Where δa is the change in the area of film (we are considering only one surface).
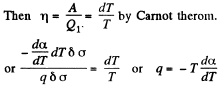
Q. 184. The surface of a soap film was increased isothermally by Δα at a temperature T. Knowing the surface tension of the soap water solution α and the temperature coefficient dα/dT, find the increment
(a) of the entropy of the film's surface layer;
(b) of the internal energy of the surface layer.
Solution. 184. As before we can calculate the heat required. It, is taking into account two sides of the soap film
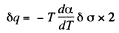
Thus 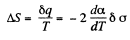
Now 




















