Irodov Solutions: Molecules and Crystals- 1 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.167. Determine the angular rotation velocity of an S2 molecule promoted to the first excited rotational level if the distance between its nuclei is d = 189 pm.
Ans. In the first excited rotational level J = 1
so 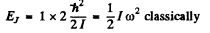
Thus 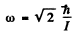
Now 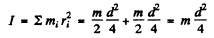
where m is the mass of the mole cub and ri is the distance of the atom from the axis.
Thus 
Q.168. For an HCl molecule find the rotational quantum numbers of two neighbouring levels whose energies differ by 7.86 meV. The nuclei of the molecule are separated by the distance of 127.5 pm.
Ans. The axis of rotation passes through die centre of mass of the HCl molecule. The distances of the two atoms from the centre of mass are
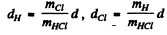
Thus I - moment of inertia about the axis
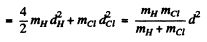
The energy difference ^between two neighbouring levels whose quantum numbers are J & J - 1 is
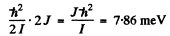
Hence J = 3 and the levels have quantum numbers 2 & 3,
Q.169. Find the angular momentum of an oxygen molecule whose rotational energy is E = 2.16 meV and the distance between the nuclei is d = 121 pm.
Ans. The angular momentum is
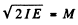
Now 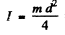 (m = mass of O2 molecule) = 1.9584 x 10-39 gm c2
(m = mass of O2 molecule) = 1.9584 x 10-39 gm c2
So 
(This corresponds to J = 3)
Q.170. Show that the frequency intervals between the neighbouring spectral lines of a true rotational spectrum of a diatomic molecule are equal. Find the moment of inertia and the distance between the nuclei of a CH molecule if the intervals between the neighbouring lines of the true rotational spectrum of these molecules are equal to Δω = 5.47.1012 s-1.
Ans. From 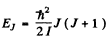
and the selection rule ΔJ = 1 or J → J - 1 for a pure rotational spectrum we get
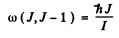
Thus transition lines are equispaced in frequency 
In the case of CH molecule
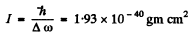
Also 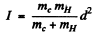
so d = 1.117 x 10-8 cm = 111.7 pm
Q.171. For an HF molecule find the number of rotational levels located between the zeroth and first excited vibrational levels assuming rotational states to be independent of vibrational ones. The natural vibration frequency of this molecule is equal to 7.79.1014 rad/s, and the distance between the nuclei is 91.7 pm.
Ans. if the vibrational frequency is to0 the excitation energy of the first vibrational level will be 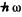 o. Thus if there are J rotational levels contained in the band between the ground state and the first vibrational excitation, then
o. Thus if there are J rotational levels contained in the band between the ground state and the first vibrational excitation, then
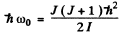
where as stated in the problem we have ignored any coupling between the two. For HF molecule
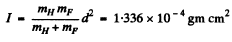
Then 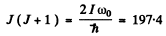
For J = 14 , J (J + 1 ) = 210 . For J - 13, J (J + 1) = 182. Thus there lie 13 levels between the ground state and the first vibrational excitation.
Q.172. Evaluate how many lines there are in a true rotational spectrum of CO molecules whose natural vibration frequency is ω = 4.09.1014 s-1 and moment of inertia I = 1.44.10-39g•cm2.
Ans. We proceed as above. Calculating 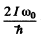 we get
we get
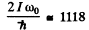
Now this must equal 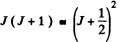
Taking the square root we get J = 33 .
Q.173. Find the number of rotational levels per unit energy interval, dN/dE, for a diatomic molecule as a function of rotational energy E. Calculate that magnitude for an iodine molecule in the state with rotational quantum number J = 10. The distance between the nuclei of that molecule is equal to 267 pm.
Ans. From the formula
 we get
we get 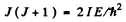
or 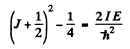
Hence 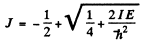
writing 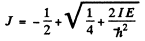
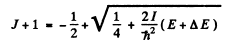
we find 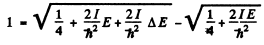
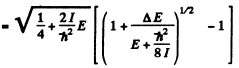
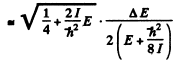
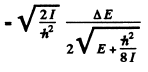
The quantity 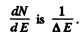 For laige E it is
For laige E it is
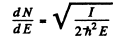
For an iodine molecule
I = mId2/ 2 = 7*57 x 10-38 gm cm2
Thus for J = 10
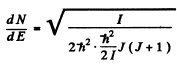
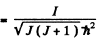
Substitution gives
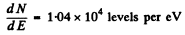
Q.174. Find the ratio of energies required to excite a diatomic molecule to the first vibrational and to the first rotational level. Calculate that ratio for the following molecules:
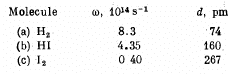
Here ω is the natural vibration frequency of a molecule, d is the distance between nuclei.
Ans. For the first rotational level
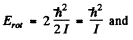
for the first vibrational level 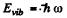
Thus 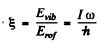
Here ω = frequency of vibration. Now
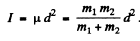
(a) For H2 molecule I = 4-58 x 10-41 gm cm2 and 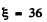
(b) For HI molecule,
I = 4.2 47 x 10-4Ogmcm2 and 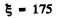
(c) For I2 molecule
I = 7.57 x 10-38gmcm2 and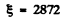
Q.175. The natural vibration frequency of a hydrogen molecule is equal to 8.25.1014 s-1, the distance between the nuclei is 74 pm, Find the ratio of the number of these molecules at the first excited vibrational level (v = 1) to the number of molecules at the first excited rotational level (J = 1) at a temperature T = 875 K. It should be remembered that the degeneracy of rotational levels is equal to 2J + 1.
Ans. The energy of the molecule in the first rotational level will be  .The ratio of tire number of molecules at tire first excited vibrational level to the number of molecules at the first excited rotational level is
.The ratio of tire number of molecules at tire first excited vibrational level to the number of molecules at the first excited rotational level is
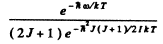
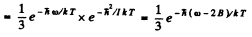
where B = h /2I
For the hydrogen molecule 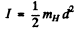
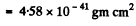
Substitution gives 3.04 x 10-4
Q.176. Derive Eq. (6.4c), making use of the Boltzmann , distribution. From Eq. (6.4c) obtain the expression for molar vibration heat capacity Cv vib of diatomic gas. Calculate Cv vib for Cl2 gas at the temperature 300 K. The natural vibration frequency of these molecules is equal to 1.064 • 1014 s- 1
Ans. By definition

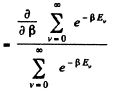
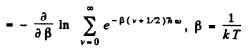
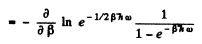
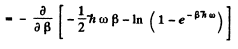
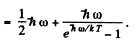
Thus for one gm mole of diatomic gas
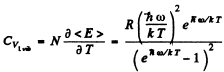
where R = Nk is the gas constant
In the present case 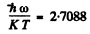
and 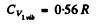
Q.177. In the middle of the rotation--vibration band of emission spectrum of HCl molecule, where the "zeroth" line is forbidden by the selection rules, the interval between neighbouring lines is Δω = = 0.79.1013s-1. Calculate the distance between the nuclei of an HCl molecule.
Ans. In the rotation vibration band the main transition is due to change in vibrational quantum number v → v - 1. Together with this rotational quantum number may change. The “Zcroeth line” 0 → 0 is forbidden in this case so the neighbouring lines arise due to 1 → 0 or 0 → 1 in the rotational quantum number. Now
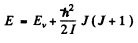
Thus 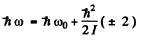
Hence 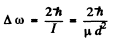
so 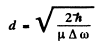
Substitution gives d = 0.128 nm .
Q.178. Calculate the wavelengths of the red and violet satellites, closest to the fixed line, in the vibration spectrum of Raman scattering by F2 molecules if the incident light wavelength is equal to λ0 = 404.7 nm and the natural vibration frequency of the molecule is ω = 2.15.1014 s-1.
Ans. If λR = wavelength of the red satellite
and λv = wavelength of the violet satellite
then 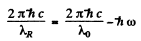
and 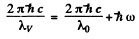
Substitution gives
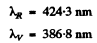
The two formulas can be combined to give
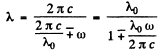
Q.179. Find the natural vibration frequency and the quasielastic force coefficient of an S2 molecule if the wavelengths of the red and violet satellites, closest to the fixed line, in the vibration spectrum of Raman scattering are equal to 346.6 and 330.0 nm.
Ans. As in the previous problem
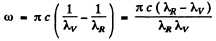 = 1.368 x 1014 rad/s
= 1.368 x 1014 rad/s
The force constant x is defined by
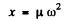
where μ= reduced mass of the S2 molecule.
Substitution gives x = 5.01N/cm
Q.180. Find the ratio of intensities of the violet and red satellites, closest to the fixed line, in the vibration spectrum of Raman scattering by Cl2 molecules at a temperature T = 300 K if the natural vibration frequency of these molecules is ω = 1.06.1014 s-1 . By what factor will this ratio change if the temperature is doubled?
Ans. The violet satellite arises from the transition 1→0 in the vibrational state of the scattering molecule while the red satellite arises from the transition 0 → 1. The intensities of these two transitions are in the ratio of initial populations of the two states i.e. in the ratio
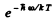
Thus 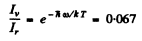
If the temperature is doubled, the rato increases to 0.259, an increase of 3.9 times.
Q.181. Consider the possible vibration modes in the following linear molecules:
(a) CO2 (O — C—O); (b) C2H2 (H—C —C—H).
Ans. (a) CO2 (O - C - O)
The molecule has 9 degrees of freedom 3 for each atom. This means that it can have up to nine frequencies. 3 degrees of freedom correspond to rigid translation, the frequency associated with this is zero as the potential energy of the system can not change under rigid translation. The P.E. will not change under rotations about axes passing through the C-atom and perpendicular to the O - C - O line. Thus there can be at most four non zero frequencies. We must look for modes different from the above.
One mode is 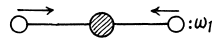
Another mode is 
These are the only collinear modes.
A third mode is doubly degenerate : 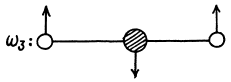
(vibration in &  to the plane of paper).
to the plane of paper).
(b) C2H2 ( H - C - C - H )
There are 4 x 3 - 3 - 2 = 7 different vibrations. There are three collinear modes.

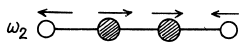

Two other doubly degenerate frequencies are

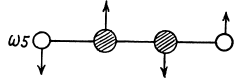
together with their counterparts in the plane  to the paper.
to the paper.
Q.182. Find the number of natural transverse vibrations of a string of length l in the frequency interval from ω to ω + dω if the propagation velocity of vibrations is equal to v. All vibrations are supposed to occur in one plane.
Ans. Suppose the string is stretched along the x axis from x = 0 to x = l with the end points fixed. Suppose y(x, t) is the transverse displacement of the element at x at time t. Then y (x, t) obeys
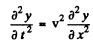
We look for a stationary wave solution of this equation
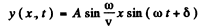
where A & δ are constants.. In this from y = 0 at x = 0. The further condition
y = 0 at x = l
implies 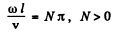
or 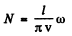
N is the number of modes of frequency ≤ ω.
Thus 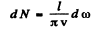
Q.183. There is a square membrane of area S. Find the number of natural vibrations perpendicular to its plane in the frequency interval from ω to ω + dω if the propagation velocity of vibrations is equal to v.
Ans. Let 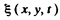 be the displacement of the element at (x , y) at time t. Then it obeys the equation
be the displacement of the element at (x , y) at time t. Then it obeys the equation
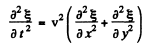
where 
We look for a solution in the form
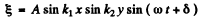
Then 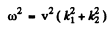
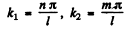
we write this as
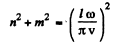
Here n, m > 0 . Each pair (n , m) determines a mode. The total mumber of modes whose frequency is ≤ ω is the area of the quadrant of a circle of radius 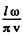 i.e.
i.e.
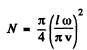
Then 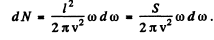
where S = I2 is the area of the membrane.
Q.184. Find the number of natural transverse vibrations of a rightangled parallelepiped of volume V in the frequency interval from ω to ω + dω if the propagation velocity of vibrations is equal to v.
Ans. For transverse vibrations of a 3-dimensional continuum (in the form of a cube say) we have the equation
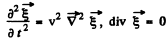
Here 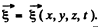 We look for solutions in the form
We look for solutions in the form
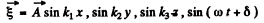
This requires 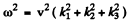
From the boundary condition that 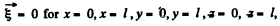 we get
we get

where n1; n2, n3 are nonzero positive integers.
We then get 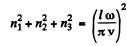
Each triplet (n1; n2, n3) determines a possible mode and the number of such modes whose frequency ≤ω is the volume of the all positive octant of a sphere of radius 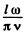 Considering also the fact that the subsidiary condition div
Considering also the fact that the subsidiary condition div  implies two independent values of
implies two independent values of 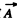 for each choice of the wave vector (k1, k2, k3)
for each choice of the wave vector (k1, k2, k3)
we find
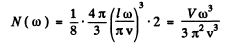
Thus
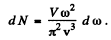
Q.185. Assuming the propagation velocities of longitudinal and transverse vibrations to be the same and equal to v, find the Debye temperature
(a) for a unidimensional crystal, i.e. a chain of identical atoms, incorporating no atoms per unit length;
(b) for a two-dimensional crystal, i.e. a plane square grid consisting of identical atoms, containing no atoms per unit area;
(c) for a simple cubic lattice consisting of identical atoms, containing no atoms per unit volume.
Ans. To determine the Debye temperature we cut off the high frequency modes in such a way as to get the total number of modes correctly.
(a) In a linear crystal with nol atoms, the number of modes of transverse vibrations in any given plane cannot exceed nol. Then
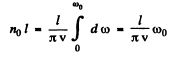
The cut off frequency ω0 is related to the Debye temperature 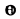 by
by
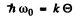
Thus 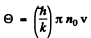
(b) In a square lattice, the number of modes of transverse oscillations cannot exceed noS.
Thus
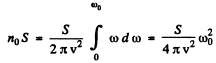
or 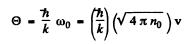
(c) In a cubic crystal, the maximum number of transverse waves must be 2n0 V (two for each atom). Thus
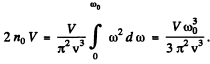
Thus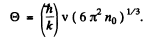
FAQs on Irodov Solutions: Molecules and Crystals- 1 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What are molecules and crystals? |  |
| 2. How are molecules and crystals different from each other? |  |
| 3. What are some examples of molecules and crystals? |  |
| 4. How are molecules and crystals studied in science? |  |
| 5. What are the applications of studying molecules and crystals? |  |






















