Irodov Solutions: Photometry & Geometrical Optics - 2 | I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE PDF Download
Q.21. The least deflection angle of a certain glass prism is equal to its refracting angle. Find the latter.
Ans. In this case we have
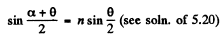
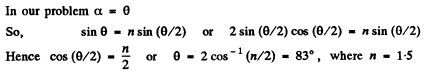
Q.22. Find the minimum and maximum deflection angles for a light ray passing through a glass prism with refracting angle θ = 60°.
Ans. In the case of minimum deviation
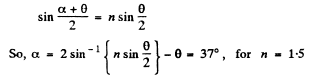
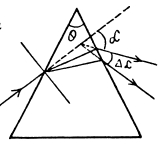
Passage of ray for grazing incidence and grazing imergence is the condition for maximum deviation (Fig.). From Fig.
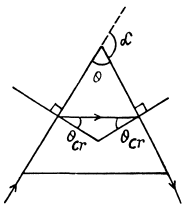
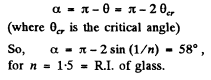
Q.23. A trihedral prism with refracting angle 60° provides the least deflection angle 37° in air. Find the least deflection angle of that prism in water.
Ans. The least deflection angle is given by the formula,
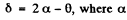 is the angle of incidence at first surface and θ is the prism angle.
is the angle of incidence at first surface and θ is the prism angle.
Alsofrom Snell’s law,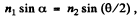 as the a ngle of refraction at first surface is equal to half the angle of prism for least deflection
as the a ngle of refraction at first surface is equal to half the angle of prism for least deflection
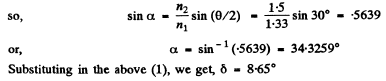
Q.24. A light ray composed of two monochromatic components passes through a trihedral prism with refracting angle θ = 60°. Find the angle Δα between the components of the ray after its passage through the prism if their respective indices of refraction are equal to 1.515 and 1.520. The prism is oriented to provide the least deflection angle.
Ans. From the Cauchy’s formula, and also experimentally the R.I. of a medium depends upon the w avelength of the mochromatic ray i.e.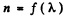 In the case of least deviation of a monochromatic ray the passage a prism, we have:
In the case of least deviation of a monochromatic ray the passage a prism, we have:
 (1)
(1)
The above equation tales us that we have n = n (α) , so we may write
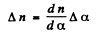 (2)
(2)
From Eqn. (1)
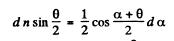
or
 (3)
(3)
From Eqn. (2) and (3)
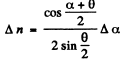
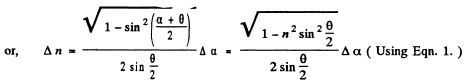
Thus 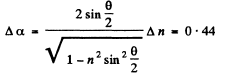
Q.25. Using Fermat's principle derive the laws of deflection and refraction of light on the plane interface between two media.
Ans. Fermat’s principle : “ The actual path of propagation of light (trajectory of a light ray ) is the path which can be followed by light with in the lest time, in comparison with all other hypothetical paths between the same two points. ” “Above statement is the original wordings of Fermat ( A famous French scientist of 17th century)”
Deduction of the law of refraction from Fermat’s principle : Let the plane S be the interface between medium 1 and medium 2 with the refractive indices 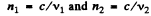 Fig.(a). Assume, as usual, that n1<n2 . Two points are g iv en - one above the plane S (point A ), the other under plane S (point B ). The various distances are :
Fig.(a). Assume, as usual, that n1<n2 . Two points are g iv en - one above the plane S (point A ), the other under plane S (point B ). The various distances are :
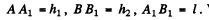 We must find the path from A to B which can be covered by light faster than it can cover any other hypothetical path. Clearly, this path must consist of two straight lines, viz, AO in medium 1 and OB in medium 2; the point O in the plane S has to be found.
We must find the path from A to B which can be covered by light faster than it can cover any other hypothetical path. Clearly, this path must consist of two straight lines, viz, AO in medium 1 and OB in medium 2; the point O in the plane S has to be found.
First of all, it follows from Fermat’s priniciple that the point O must lie on the intersection of S and a plane P, which is perpendicular to S and passes through A and B.
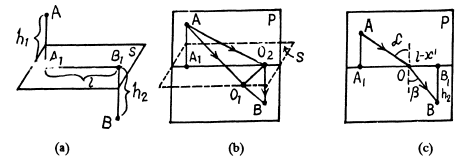
Indeed, let us assume that this point does not lie in the plane P; let this be point 0 1 in Fig. (b). Drop the perpendicular O2 from O1 onto P . Since AO2 < AO1 and BO2< BO1 it is clear that the time required to traverse AO2B is less than that needed to cover the path AO1B.
Thus, using Fermat’s principle, we see that the first law of refraction is observed : the incident and the refracted rays lie in the same plane as the perpendicular to the interface at the point
where the ray is refracted. This plane is the plane P in Fig. (b); it is called the plane of incidence.
Now let us consider light rays in the plane of incidence Fig. (c). Designate
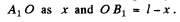 The time it takes a ray to travel from A to O and then from O to B is
The time it takes a ray to travel from A to O and then from O to B is
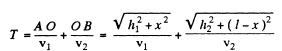 (1)
(1)
The time depends on the value of x. According tofermat's principle, the value of x must m inim ize the time T. A t this value of x the derivative dT/dx equals zero :
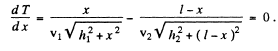 (2)
(2)
Now,
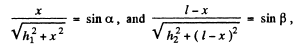
Consequently,
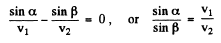
So,
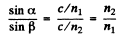
Note : Fermat himself could not use Eqn. 2. as mathematical analysis was developed later by Newton and Leibniz. To deduce the law of the refraction of light, Fermat used his own maximum and minimum method of calculus, which, in fact, corresponded to the subsequently developed method of finding the minimum (maximum) of a function by differentiating it and equating the derivative to zero.
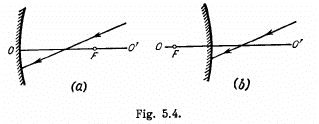
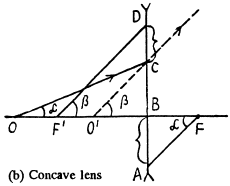
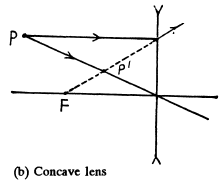
Q.26. By means of plotting find: (a) the path of a light ray after reflection from a concave and convex spherical mirrors (see Fig. 5.4, where F is the focal point, 00' is the optical axis);
(b) the positions of the mirror and its focal point in the cases illustrated in Fig. 5.5, where P and P' are the conjugate points.
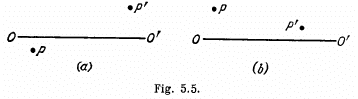
Ans. (a) Look for a point O' on the axis such that O' F and O' P make equal angles with O' O.
This determines the position of the mirror. Draw a ray from P parallel to the axis. This must on reflection pass through F. The intersection of the reflected ray with principal axis determines the focus.
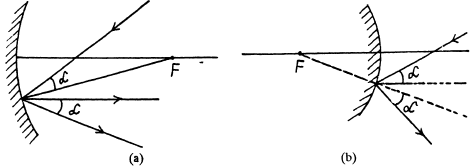
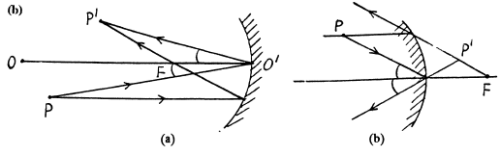
(b) Suppose P is the object and F is the image. Then the mirror is convex because the image is virtual, erect & dim inished. Look for a point X (between P & F ) on the axis such that PX and F'X make equal angle with the axis.
Q.27. Determine the focal length of a concave mirror if:
(a) with the distance between an object and its image being equal to l = 15 cm, the transverse magnification β = —2.0;
(b) in a certain position of the object the transverse magnification is β1 = —0.50 and in another position displaced with respect to the former by a distance l = 5.0 cm the transverse magnification β2 = = —0.25.
Ans. (a) From the mirror formula,
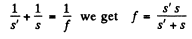 (1)
(1)
In accordance with the problem 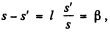
From these two relations, we get : 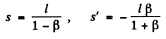
Substituting it in the Eqn. (1),
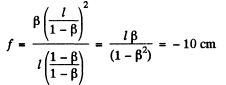
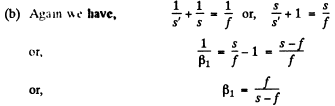 (2)
(2)
Now , it is clear from the above equation, that for smaller p , s must be large, so the object is displaced away from the mirror in second position.
i.e.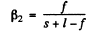 (3)
(3)
Eliminating 5 from the Eqn. (2) and (3), we get,
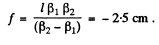
Q.28. A point source with luminous intensity I0 = 100 cd is positioned at a distance s = 20.0 cm from the crest of a concave mirror with focal length f = 25.0 cm. Find the luminous intensity of the reflected ray if the reflection coefficient of the mirror is p = 0.80.
Ans. For a concave mirror as usual
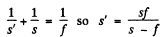
(In coordinate convention s = - s is negative 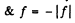 is also negative.)
is also negative.)
If A is the area of the mirror (assumed sm all) and the object is on the principal axis, then the light incident on the mirror per second is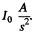
This follows from the definition of luminous intensity as light emitted per second per unit solid angle in a given direction and the fact that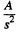 is the solid angle subtended by the mirror at the source. of this a fraction p is reflected so if I is the luminous intensity of the image,
is the solid angle subtended by the mirror at the source. of this a fraction p is reflected so if I is the luminous intensity of the image,
then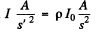
Hence
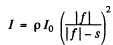
(Because our convention makes f - ve for a concave mirror, we have to write 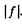 )
)
Substitution gives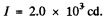
Q.29. Proceeding from Fermat's principle derive the refraction formula for paraxial rays on a spherical boundary surface of radius R between media with refractive indices n and n'.
Ans. For O1 to be the image, the optical paths of all rays OAO1 must be equal upto terms o f leading order in h Thus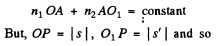

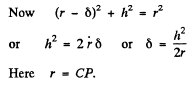
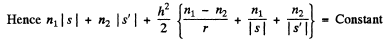
Since this must hold for all h, we have
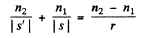
From our sign convention,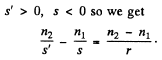
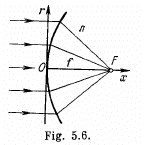
Q.30. A parallel beam of light falls from vacuum on a surface enclosing a medium with refractive index n (Fig. 5.6). Find the shape of that surface, x (r), if the beam is brought intofocus at the point F at a distance f from the crest O. What is the maximum radius of a beam that can still be focussed?
Ans. All rays focusing at a point must have traversed the same optical path. Thus
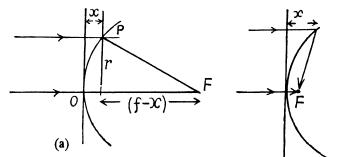
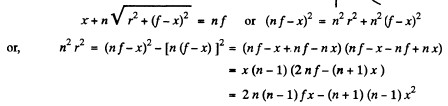


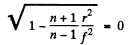 (A)
(A)
because the expression under the radical sign must be non-negative, which gives the maximum value of r.
Hence from Eqn.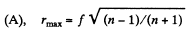
Q.31. A point source is located at a distance of 20 cm from the front surface of a symmetrical glass biconvex lens. The lens is 5.0 cm thick and the curvature radius of its surfaces is 5.0 cm. How far beyond the rear surface of this lens is the image of the source formed?
Ans. As the given lense has significant thickness, the thin lense, formula cannote be used.
For refraction at the front surface from the formula 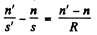
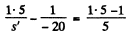
On simplifying we get , s' = 30 cm.
Thus the image l' produced by the front surface behaves as a virtual source for the rear surface at distance 25 cm from it, because the thickness of the lense is 5 cm. Again from the refraction formula at cerve surface
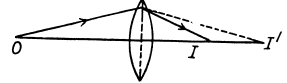
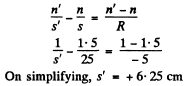
Thus we get a real image l at a distance 6- 25 cm beyond the rear surface (Fig.).
Q.32. An object is placed in front of convex surface of a glass piano-convex lens of thickness d = 9.0 cm. The image of that object is formed on the plane surface of the lens serving as'a screen. Find:
(a) the transverse magnification if the curvature radius of the lens's convex surface is R = 2.5 cm;
(b) the image illuminance if the luminance of the object is L = 7700cd/m2 and the entrance aperture diameter of the lens is D = 5.0 mm; losses of light are negligible.
Ans. (a) The formation of the image of a source 5, placed at a distance u from the pole of the convex surface of plano-convex lens of thickness d is shown in the figure.

But in this case optical path of the light, corresponding to the distance v in the medium is v/n, so the magnification produced will be,
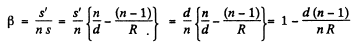
Substituting the values, we get magnification β = - 0-20.
(b) If the transverse area of the object is A (assumed small), the area of the image is β2A.
We shall assume that 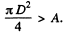 Then light falling on the Jens is
Then light falling on the Jens is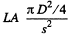 from the definition of luminance (See Eqn. (5.1c) of the book; here
from the definition of luminance (See Eqn. (5.1c) of the book; here
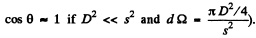 Then the illum inance of the image is
Then the illum inance of the image is
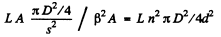
Substitution gives 42 lx.
Q.33. Find the optical power and the focal lengths
(a) of a thin glass lens in liquid with refractive index no = 1.7 if its optical power in air is 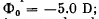
(b) of a thin symmetrical biconvex glass lens, with air on one side and water on the other side, if the optical power of that lens in air is 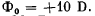
Ans. (a) Optical power of a thin lens o f R.I. n in a m edium w ith R I . n0 is given by :
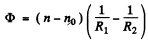 (A)
(A)
From Eqn.(A), when the lens is placed in air :
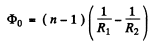 (1)
(1)
Similarly from Eqn.(A), when the lens is placed in liquid :
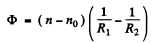 (2)
(2)
Thus from Eqns (1) and (2)
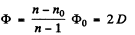
The second focal length, is given by
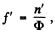 where n is the R.I. of the medium in which it is placed.
where n is the R.I. of the medium in which it is placed.
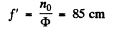
(b) Optical power of a thin lens of RI. n placed in a medium of RI. no is given by :
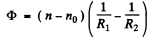 (A)
(A)
For a biconvex lens placed in airmedium from Eqn. (A)
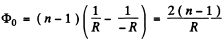 (1)
(1)
where R is the radius of each curve surface of the lens
Optical power of a spherical refractive surface is given by :
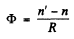 (B)
(B)
For the rear surface of the lens which divides air and glass medium
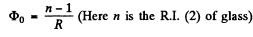
Similarly for the front surface which divides wati nd glass medium
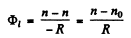 (3)
(3)
Hence the optical power of the given optical system
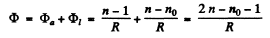 (4)
(4)
From Eqns (1) and (4)
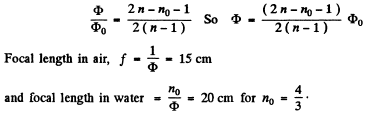
Q.34. By means of plotting find: (a) the path of a ray of light beyond thin converging and diverging lenses (Fig. 5.7, where 00' is the optical axis, F and F' are the front and rear focal points);
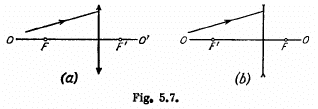
(b) the position of a thin lens and its focal points if the position of the optical axis 00' and the positions of the cojugate points P, P' (see Fig. 5.5) are known; the media on both sides of the lenses are identical; (c) the path of ray 2 beyond the converging and diverging lenses (Fig. 5.8) if the path of ray I and the positions of the lens and of its
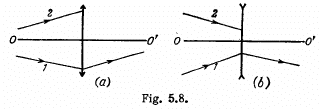
optical axis 00' are all known; the media on both sides of the lenses are identical.
Ans. (a) Clearly the media on the sides are different. The front focus F is the position of the object (virtual or real) for which the image is formated at infinity. The rear focus F' is the position of the image (virtual or real) of the object at infinity, (a) Figures 5.7 (a) & (b). This geometrical construction ensines that the second of the equations (5.1g) is obeyed
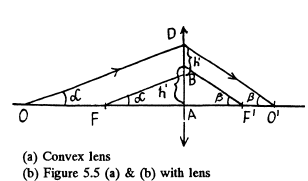

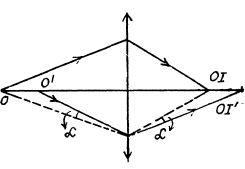
(c) Figure (5.8) (a) & (b).
Clearly, the important case is that when the rays (1) & (2) are not symmetric about the principal axis, otherwise the figure can be completed by reflection in the principal axis. Knowing one path we know the path of all rays connecting the two points. For a different object. We proceed as shown below, we use the fact that a ray incident at a given height above the optic centre suffers a definite deviation.
The concave lens can be discussed similarly.
Q.35. A thin converging lens with focal length f = 25 cm projects the image of an object on a screen removed from the lens by a distance 1=5.0 m. Then the screen was drawn closer to the lens by a distance Δl = 18 cm. By what distance should the object be shifted for its image to become sharp again?
Ans. Since the image is formed on the screen, it is real, so for a conversing lens object is in the incident side.
Let S1 and S2 be the magnitudes of the object distance in the first and second case respectively. We have the lens formula
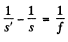 (1
(1
In the first case from Eqn. (1))
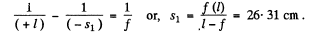
Similarly from Eqn.(l) in the second case
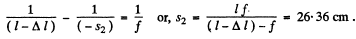
Thus the sought distance 
Q.36. A source of light is located at a distance l = 90 cm from a screen. A thin converging lens provides the sharp image of the source when placed between the source of light and the screen at two positions. Determine the focal length of the lens if (a) the distance between the two positions of the lens is Δl = = 30 cm; (b) the transverse dimensions of the image at one position of the lens are η = 4.0 greater than those at the other position.
Ans. The distance between the object and the image is l. Let x = distance between the object and the lens. Then, since the image is real, we have in our convention, 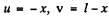
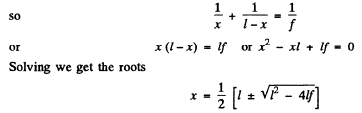
(We must have / > 4f for real roots.)
(a) If the distance between the two positions of the lens is Δl, then clearly
(b) The two roots are conjugate in the sense that if one gives the object distance the other gives the corresponding image distance (in both cases). Thus the magnifications are
The ratio of these magnification being η we have
Q.37. A thin converging lens is placed between an object and a screen whose positions are fixed. There are two positions of the lens at which the sharp image of the object is formed on the screen. Find the transverse dimension of the object if at one position of the lens the image dimension equals h' = 2.0 mm and at the other, h" = 4.5 mm.
Ans. We know from the previous problem that the two magnifications are reciprocals of each other (B' β" = 1). If h is the size of the object then h' = β' h and
H ence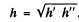
Q.38. A thin converging lens with aperture ratio D : f = 1: 3.5 (D is the lens diameter, f is its focal length) provides the image of a sufficiently distant object on a photographic plate. The object luminance is L = 260 cd/m2. The losses of light in the lens amount to α = 0.10. Find the illuminance of the image.
Ans. Refer to problem 5.32 (b). If A is the area of the object, then provided the angular diameter of the object at the lens is much smaller than other relevant angles like 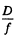 we calculate the light falling on the lens as
we calculate the light falling on the lens as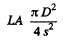
where u2 is the object distance squared. If β is the transverse magnification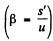 then the area of the image is β2A. Hence the illuminance of the image (also taking account of the light lost in the lens)
then the area of the image is β2A. Hence the illuminance of the image (also taking account of the light lost in the lens)
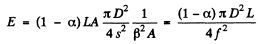
since s' = f for a distant object Substitution gives E = 15 lx.
Q.39. How does the luminance of a real image depend on diameter D of a thin converging lens if that image is observed (a) directly; (b) on a white screen backscattering according to Lambert's law?
Ans. (a) If s = object distance, s' = average distance, L = luminance of the sounce, ΔS = area of the source as sumed to be a plane surface held normal to the principal axis, then we find for the flux 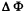 incident on the lens
incident on the lens
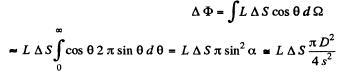
Here we are assuming D « s, and ignoring the variation of L since a is small
Then if L' is the luminance of the image, and  is the area of the image then similarly
is the area of the image then similarly
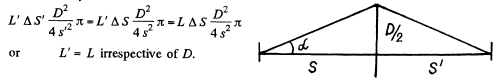
(b) In this case the image on the white screen from a Lambert source. Then if its luminance is L0 its luminosity will be the πL0 and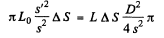
or 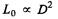
since s' depends on f, s but not on D.
Q.40. There are two thin symmetrical lenses: one is converging, with refractive index n1 = 1.70, and the other is diverging with refractive index n2 = 1.51. Both lenses have the same curvature radius of their surfaces equal to R = 10 cm. The lenses were put close together and submerged into water. What is the focal length of this system in water?
Ans. Focal length of the converging lens, when it is submerged in water of R.I. n0 (say) :
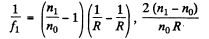 (1)
(1)
Similarly, the focal length of diverging lens in water.
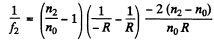 (2)
(2)
Now, when they are put together in the water, the focal length of the system,
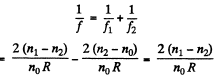
or,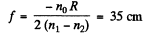
FAQs on Irodov Solutions: Photometry & Geometrical Optics - 2 - I. E. Irodov Solutions for Physics Class 11 & Class 12 - JEE
| 1. What is photometry in the context of geometrical optics? |  |
| 2. How does photometry help in understanding the behavior of light? |  |
| 3. What are the key principles of geometrical optics? |  |
| 4. How can photometry be applied in practical applications? |  |
| 5. What are some commonly used photometric units and their definitions? |  |
















